Четырёхмерный многогранник

Четырёхмерный многогранник — многогранник в четырёхмерном пространстве[1][2]. Многогранник является связанной замкнутой фигурой, состоящей из многогранных элементов меньшей размерности — вершин, рёбер, граней (многоугольников) и ячеек (трёхмерных многогранников). Каждая грань принадлежит ровно двум ячейкам.

Графы шести выпуклых правильных четырёхмерных многогранников
{3,3,3} {3,3,4} {4,3,3}

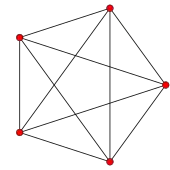Пятиячейник
4-симплекс
Шестнадцати-
ячейник
Ортоплекс
4-ортоплекс
Тессеракт
4-куб
{3,4,3} {5,3,3} {3,3,5}

Октаплекс
Двадцатичетырёхъячейник
Додекаплекс
Стодвадцатиячейник
Тетраплекс
Шестисотячейник

Двумерным аналогом четырёхмерных многогранников является многоугольник, а трёхмерным аналогом является трёхмерный многогранник.

Топологически четырёхмерные многогранники тесно связаны с однородными сотами, такими как кубические соты, замощающие трёхмерное пространство. Подобным образом трёхмерный куб связан с бесконечными двумерными квадратными сотами. Выпуклые четырёхмерные многогранники могут быть разрезаны и развёрнуты в виде развёрток в трёхмерном пространстве.

Определение

Четырёхмерный многогранник является замкнутой четырёхмерной фигурой. Он состоит из вершин (угловых точек), рёбер, граней и ячеек. Ячейка — это трёхмерный аналог грани и является трёхмерным многогранником. Каждая двумерная грань должна соединять ровно две ячейки, аналогично тому, как рёбра трёхмерного многогранника соединяют ровно две грани. Подобно другим многогранникам элементы четырёхмерного многогранника не могут быть разделены на два или более множеств, которые также являются четырёхмерными многогранниками, то есть он не является составным.

Наиболее известным четырёхмерным многогранником является тессеракт (гиперкуб), четырёхмерный аналог куба.

Визуализация
Примеры представления двадцатичетырёхъячейника
Срез Развёртка
Проекции
Шлегель 2D ортогональная 3D ортогональная

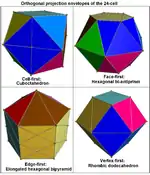Четырёхмерные многогранники невозможно представить в трёхмерном пространстве ввиду лишней размерности. Для визуализации используется ряд техник.

Ортогональная проекция

Ортоганальные проекции можно использовать для показа различных симметрий четырёхмерного многогранника. Проекции можно представить в виде двумерных графов, а можно представить в виде трёхмерных тел в качестве проективных оболочек.

Перспективная проекция

Точно также как трёхмерные фигуры можно спроецировать на плоский лист, четырёхмерные фигуры можно спроецировать в трёхмерное пространство или даже на плоскость. Распространённым видом проекции является диаграмма Шлегеля, использующая стереографическую проекциию точек на поверхность 3-сферы в трёхмерном пространстве, соединёнными в трёхмерном пространстве прямыми рёбрами, гранями и ячейками.

Срез

Точно так же, как разрез многогранника выявляет поверхность разреза, срез четырёхмерного многогранника даёт «гиперповерхность» в трёхмерном пространстве. Последовательность таких срезов можно использовать для понимания всей фигуры. Лишнюю размерность можно приравнять ко времени для образования анимации этих сечений.

Развёртки

Развёртка четырёхмерного многогранника состоит из многогранных ячеек, соединённых гранями и располагающихся в трёхмерном пространстве, точно так же, как многоугольные грани развёртки трёхмерного многогранника соединены рёбрами и располагаются все в одной плоскости.

Топологические характеристики
Тессеракт в виде диаграммы Шлегеля

Топология любого заданного четырёхмерного многогранника определяется его числами Бетти и коэффициентами кручения[3].

Значение эйлеровой характеристики, используемой для характеристики многогранников, не обобщается должным образом на высшие размерности и равно нулю для всех четырёхмерных многогранников, какова бы ни была нижележащая топология. Это несоответствие эйлеровой характеристики для достоверного различения разных топологий в высоких размерностях ведёт к появлению более утончённых чисел Бетти[3].

Подобным образом понятие ориентируемости многогранника недостаточно для характеристики закручивания поверхностей тороидальных многогранников, что приводит к использованию коэффициентов кручения[3].

Классификация

Критерии

Четырёхмерные многогранники можно классифицировать по свойствам, таким как «выпуклость» и «симметрия»[3].

  • Четырёхмерный многогранник является выпуклым, если его границы (включая ячейки, (трёхмерные) грани и рёбра) не пересекают себя (в принципе, грани многогранника могут проходить внутри оболочки) и отрезки, соединяющие любые две точки четырёхмерного многогранника, содержатся полностью внутри него.. В противном случае многогранник считается невыпуклым. Самопересекающиеся четырёхмерные многогранники известны также как звёздчатые многогранники по аналогии с похожими на звёзды формами невыпуклых многогранников Кеплера — Пуансо.
  • Четырёхмерный многогранник является правильным, если он транзитивен относительно его флагов. Это значит, что все его ячейки являются конгруэнтными правильными многогранниками, а также все его вершинные фигуры конгруэнтны другому виду правильных многогранников.
  • Выпуклый четырёхмерный многогранник является полуправильным, если он имеет группу симметрии, при которой все вершины эквивалентны (вершинно транзитивны) и ячейки являются правильными многогранниками. Ячейки могут быть двух и более видов, при условии, что они имеют один и тот же вид граней. Существует только 3 таких фигуры, найденные Торолдом Госсетом в 1900 году: полноусечённый пятиячейник, полноусечённый шестисотячейник и плосконосый двадцатичетырёхячейник.
  • Четырёхмерный многогранник является однородным, если он имеет группу симметрии, при которой все вершины эквивалентны и ячейки являются однородными многогранниками. Грани (2-мерные) однородного 4-многогранника должны быть правильными многоугольниками.
  • Четырёхмерный многогранник является равнорёберным многогранником[4], если он вершинно транзитивен и имеет рёбра одной длины. То есть разрешаются неоднородные ячейки, например, выпуклые многогранники Джонсона.
  • О правильном четырёхмерном многограннике, являющимся к тому же выпуклым, говорят как о правильном выпуклом четырёхмерном многограннике.
  • Четырёхмерный многогранник является призматическим, если он представляет собой прямое произведение двух и более многогранников меньшей размерности. Призматический четырёхмерный многогранник является однородным, если его сомножители в прямом произведении однородны. Гиперкуб является призматическим (произведение двух квадратов или куба и отрезка), но рассматривается отдельно, поскольку он имеет более высокую симметрию, чем симметрии, унаследованные от сомножителей.
  • Мозаика или соты в трёхмерном пространстве — это разложение трёхмерного евклидового пространства на повторяющуюся решётку многогранных ячеек. Такие мозаики или замощения бесконечны и не ограничены «4D»-объёмом, так что являются примерами бесконечных четырёхмерных многогранников. Однородная мозаика трёхмерного пространства — это мозаика, в которой вершины конгруэнтны и связаны кристаллографической группой, а ячейки являются однородными многогранниками.

Классы

Следующий список различных категорий четырёхмерных многогранников классифицирован согласно критериям, изложенным выше:

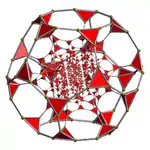
Усечённый стодвадцатиячейник является одним из 47 выпуклых непризматических однородных четырёхмерных многогранников

Однородный четырёхмерный многогранник (вершинно транзитивный).

  • Выпуклые однородные четырёхмерные многогранники (64, плюс два бесконечных семейства)
    • 47 непризматических выпуклых однородных четырёхмерных многогранника включают:
    • Призматические однородные многогранники:
      • {} × {p, q} : 18 многогранных призм (включая кубические гиперпризмы, правильные гиперкубы);
      • Призмы, построенные на антипризмах (бесконечное семейство);
      • {p} × {q} : Дуопризмы (бесконечное семейство).
  • Невыпуклые однородные четырёхмерные многогранники (10 + неизвестно):
    Большой великий стодвадцатиячейник, имея 600 вершин, является наибольшим из 10 правильных звёздчатых четырёхмерных многогранников

Другие выпуклые четырёхмерные многогранники:

  • Многогранная пирамида;
  • Многогранная призма.
Правильные кубические соты являются единственным правильным бесконечным четырёхмерным многогранником в евклидовом трёхмерном пространстве

Бесконечные однородные 4-мерные многогранники в евклидовом 3-мерном пространстве (однородные замощения выпуклыми однородными ячейками):

  • 28 выпуклых однородных сот (однородных выпуклых замощений), включая:

Бесконечные однородные четырёхмерные многогранники гиперболического трёхмерного пространства (однородные замощения выпуклыми однородными ячейками):

Двойственные однородные четырёхмерные многогранники (ячейно транзитивные):

  • 41 единственно возможных двойственных однородных четырёхмерных многогранника;
  • 17 единственно возможных двойственных однородных многогранных призм;
  • бесконечное семейство двойственных выпуклых однородных дуопризм (с неправильными тетраэдральными ячейками);
  • 27 единственно возможных двойственных однородных сот, включая:
    • Ромбические додекаэдральные соты;
    • Равногранные тетраэдральные соты.

Другие:

  • Структура Уэйра-Фелана периодических заполняющих пространство сот с неправильными ячейками.
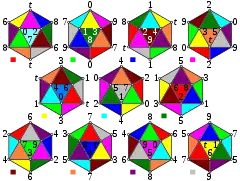
Одиннадцатиячейник является абстрактным правильным четырёхмерным многогранником, существующим в вещественной проективной плоскости. Его можно представить, нарисовав его 11 полуикосаэдральных вершин и ячеек в цвете

Абстрактные правильные четырёхмерные многогранники:

Эти категории включают только четырёхмерные многогранники с высокой степенью симметрии. Возможно существование многих других четырёхмерных многогранников, но они не изучались столь интенсивно, как перечисленные выше.

См. также
  • Правильный четырёхмерный многогранник
  • 3-сфера является другой широко обсуждаемой фигурой, располагающейся в четырёхмерном пространстве. Но она не является четырёхмерным многогранником, поскольку не ограничена многогранными ячейками.
  • Дуоцилиндр является фигурой в четырёхмерном пространстве, связанной с дуопризмами, хотя это тоже не многогранник.

Примечания
  1. Vialar, 2009, p. 674.
  2. Capecchi, Buscema, D'Amore, 2010, p. 598.
  3. Richeson, D.; Euler’s Gem: The Polyhedron Formula and the Birth of Topoplogy, Princeton, 2008.
  4. В английском языке используется слово scaliform, образованное от двух слов — scale (многозначное слово, здесь — размер, шкала) и uniform (однородный). Название предложил Джонатан Боуэрс (Jonathan Bowers)
  5. Uniform Polychora, Norman W. Johnson (Wheaton College), 1845 cases in 2005

Литература
  • T. Vialar. Complex and Chaotic Nonlinear Dynamics: Advances in Economics and Finance. — Springer, 2009. — С. 674. — ISBN 978-3-540-85977-2.
  • V. Capecchi, P. Capecchi, M. Buscema, B. D'Amore. Applications of Mathematics in Models, Artificial Neural Networks and Arts. — Springer, 2010. — С. 598. — ISBN 978-90-481-8580-1. — doi:10.1007/978-90-481-8581-8.
  • H.S.M. Coxeter:
    • H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
    • H.S.M. Coxeter. Regular Polytopes. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.
  • H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H. S. M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380—407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559—591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
  • J.H. Conway, M.J.T. Guy. Proceedings of the Colloquium on Convexity at Copenhagen. — 1965. — С. 38-39.
  • Norman Johnson. The Theory of Uniform Polytopes and Honeycombs. — Ph.D. Dissertation. — University of Toronto, 1966.
  • Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.