Четырёхмерное пространство
Четырёхмерное пространство (обозначения: 4D или ) — математический объект, обобщающий свойства трёхмерного пространства. Его не следует путать с четырёхмерным пространством-временем теории относительности (пространством Минковского).

Алгебраически четырёхмерное пространство может быть построено как множество векторов с четырьмя вещественными координатами. Геометрически в простейшем случае четырёхмерное пространство рассматривается как евклидово пространство четырёх измерений, в более общем рассмотрении оно имеет неевклидову метрику, переменную от точки к точке.
Четырёхмерное пространство можно также представить как бесконечное количество трёхмерных пространств, расположенных по четвёртой оси координат, так же, как трёхмерный мир состоит из бесконечного количества двумерных плоскостей, размещённых вдоль третьей оси.
Далее для краткости приставка 4- указывает на четырёхмерность следующего за ней понятия. Сокращение 3D обозначает трёхмерное пространство.
Геометрия четырёхмерного евклидова пространства
Векторы
Точки и векторы в трёхмерном пространстве с заданной системой координат определяются тремя координатами; аналогично точки и векторы в 4D имеет четыре координаты. Пример 4-вектора:
Сложение и вычитание векторов происходит покомпонентно, как и в трёх измерениях. Скалярное произведение 4-векторов определяется формулой:
Как и в трёхмерном случае, квадратный корень из скалярного квадрата вектора есть его норма: . Угол между векторами определяется по той же формуле, что и в трёхмерном пространстве:
В отличие от трёхмерного случая, в 4D нет прямого аналога векторного произведения. Вместо него можно использовать бивектор внешнего произведения.
Стереометрия
Геометрия тел в 4D гораздо сложнее, чем в 3D. В трёхмерном пространстве многогранники ограничены двумерными многоугольниками (гранями), соответственно в 4D существуют 4-многогранники, ограниченные 3-многогранниками.
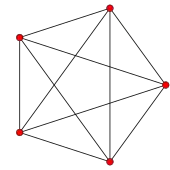
В 3D существуют 5 правильных многогранников, известных как Платоновы тела. В 4-х измерениях есть 6 правильных выпуклых 4-многогранников, это аналоги Платоновых тел. Если ослабить условия правильности, получатся дополнительно 58 выпуклых полуправильных 4-многогранников, аналогичных 13 полуправильным Архимедовым телам в трёх измерениях. Если снять условие выпуклости, получатся дополнительно ещё 10 невыпуклых регулярных 4-многогранников.
| A4, [3,3,3] | B4, [4,3,3] | F4, [3,4,3] | H4, [5,3,3] | ||
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
В трёхмерном пространстве кривые могут образовывать узлы, а поверхности не могут (если они не являются самопересекающимися). В 4D положение меняется: узлы из кривых можно легко развязать, используя четвёртое измерение, а из двумерных поверхностей можно сформировать нетривиальные (не самопересекающиеся) узлы[1]. Поскольку эти поверхности двумерны, они могут образовывать более сложные узлы, чем в 3-мерном пространстве. Примером такого узла из поверхностей является широко известная «бутылка Клейна».
Способы визуализации четырёхмерных тел
Проекции

Проекция — изображение n-мерной фигуры на так называемом картинном (проекционном) подпространстве способом, представляющим собой геометрическую идеализацию оптических механизмов. Так, например, в реальном мире, контур тени предмета — это проекция контура этого предмета на плоскую или приближённую к плоской поверхность — проекционной плоскости. При рассмотрении проекций четырёхмерных тел проецирование осуществляется на трёхмерное пространство, то есть, по отношению к четырёхмерному пространству, на картинное (проекционное) подпространство (то есть пространство, с числом измерений или, иначе говоря, размерностью, на 1 меньшей, чем число измерений (размерность) самого того пространства, в котором находится проецируемое тело). Проекции бывают параллельными (проекционные лучи параллельны) и центральными (проекционные лучи исходят из некоторой точки). Иногда применяются также стереографические проекции. Стереографическая проекция — центральная проекция, отображающая n-1-сферу n-мерного шара (с одной выколотой точкой) на гиперплоскость n-1. N-1-сферой (гиперсферой) называют обобщение сферы, гиперповерхность в n-мерном (с числом измерений или размерностью n) евклидовом пространстве, образованная точками, равноудалёнными от заданной точки, называемой центром сферы, гипершаром — тело (область гиперпространства), ограниченное гиперсферой.
Сечения
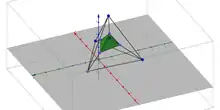
Сечение — изображение фигуры, образованной рассечением тела плоскостью без изображения частей за этой плоскостью. Подобно тому, как строятся двухмерные сечения трёхмерных тел, можно построить трёхмерные сечения четырёхмерных тел, причём также как двухмерные сечения одного и того же трёхмерного тела могут сильно отличаться по форме, так и трёхмерные сечения будут ещё более разнообразными, так как будут менять и количество граней, и количество сторон у каждой грани сечения. Построение трёхмерных сечений сложнее, чем создание проекций, поскольку проекции можно (особенно для несложных тел) получить по аналогии с двухмерными, а сечения строятся только логическим путём, при этом рассматривается каждый конкретный случай отдельно.
Развёртки
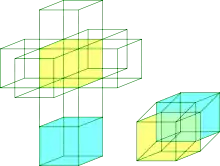
Развёртка гиперповерхности — фигура, получающаяся в гиперплоскости (подпространстве) при таком совмещении точек данной гиперповерхности с этой плоскостью, при котором длины линий остаются неизменными. Аналогично тому, как трёхмерные многогранники можно сложить из бумажных развёрток, многомерные тела могут быть представлены в виде развёрток своих гиперповерхностей.
Попытки научного исследования
После того, как Бернхард Риман в 1853 году теоретически обосновал возможность существования n-мерного пространства, попытки обнаружить и исследовать гипотетические дополнительные измерения пространства неоднократно предпринимали как серьёзные учёные, так и всевозможные оккультисты и эзотерики[2]. Английский математик XIX века Чарльз Хинтон опубликовал ряд книг на эту тему и глубоко изучил проблему визуализации. По его мнению, наш трёхмерный мир разделяет невидимый нам четырёхмерный на две части (аналогично тому, как плоскость делит пополам наше пространство). Эти части он условно назвал по-гречески Ана (верхний мир) и Ката (нижний мир)[3].
Во второй половине XIX — начале XX века изучение этой темы было основательно дискредитировано спиритизмом, который рассматривал невидимые измерения как обиталище душ умерших, а миры Ана и Ката зачастую отождествлялись с адом и раем; свой вклад внесли философы и теологи. Вместе с тем вопрос привлекал внимание таких крупных учёных, как физики Уильям Крукс и Вильгельм Вебер, астроном Иоганн Карл Фридрих Цёлльнер (автор книги «Трансцендентальная физика»), нобелевские лауреаты лорд Рэлей и Джозеф Джон Томсон[4]. Русский физик Дмитрий Бобылёв написал энциклопедическую статью по теме.
Физик и философ Эрнст Мах неоднократно высказывал предположение, что число измерений пространства не обязательно равно трём, например, в статье 1872 года: «Что до сих пор не удалось создать удовлетворительную теорию электричества, это зависит, может быть, от того, что электрические явления непременно хотели объяснить молекулярными процессами в пространстве с тремя измерениями» В 1914 году Гуннар Нордстрём опубликовал свой вариант новой теории тяготения, основанный на четырёхмерном пространстве в пятимерном пространстве-времени (модель 4+1); эта теория не соответствовала наблюдениям и была отвергнута. В 1920-е годы появилась близкая по геометрической структуре (та же модель 4+1) теория Калуцы — Клейна, объединяющая общую теорию относительности Эйнштейна и электромагнетизм Максвелла, все эффекты объяснялись геометрическими свойствами пространства и времени. В современной теории струн пространство-время имеет 11 измерений, см. старшие размерности[5].
В литературе
Тема дополнительных измерений пространства и близкая к ней тема параллельных миров давно стала популярной в фантастической и философской литературе. Герберт Уэллс, одним из первых описавший путешествие во времени, во многих других своих произведениях затронул также и невидимые измерения пространства: «Чудесное посещение», «Замечательный случай с глазами Дэвидсона», «Хрустальное яйцо», «Украденное тело», «Люди как боги», «История Платтнера». В последнем рассказе человек, выброшенный катастрофой из нашего мира и затем вернувшийся, претерпевает пространственное отражение — например, сердце у него оказывается с правой стороны (впрочем, из-за некоторых различий химических свойств"левых" и "правых" молекул белков, такой организм может оказаться нежизнеспособным). Владимир Набоков описал аналогичное изменение пространственной ориентации в романе «Смотри на арлекинов!» (1974). В научной фантастике второй половины XX века четвёртое измерение использовали такие крупные писатели, как Айзек Азимов, Артур Кларк, Фредерик Пол, Клиффорд Саймак и многие другие. Создание четырёхмерного тессеракта лежит в основе сюжета рассказа Роберта Хайнлайна, названного в русском переводе «Дом, который построил Тил»[6].
Валерий Брюсов в 1924 году написал стихотворение «Мир N измерений»[7].
В мистической литературе четвёртое измерение нередко описывается как обиталище демонов или душ умерших. Эти мотивы встречаются, например, у Джорджа Макдональда (роман «Лилит»), в нескольких рассказах Амброза Бирса, в рассказе А. П. Чехова «Тайна». Математик-теософ Пётр Успенский развивал идеи как о мистическом понимании четвёртого измерения, так и о его трактовке с научной точки зрения. В романе Дж. Конрада и Ф. М. Форда «Наследники» (The Inheritors, 1901) обитатели четвёртого измерения пытаются захватить нашу Вселенную[6].
В изобразительном искусстве
Концепция четвёртого измерения оказала значительное влияние на изобразительное искусство. Роль перспективы снизилась; например, кубисты (Пикассо, Метценже и другие) в своих картинах часто изображали людей и предметы одновременно в различных ракурсах, тем самым как бы добавляя им измерения (см., например, картину «Авиньонские девицы»). Гийом Аполлинер в 1913 году писал[8].:
Сегодня учёные больше не ограничивают себя тремя измерениями Евклида. И художники, что совершенно естественно (хотя кто-то и скажет, что только благодаря интуиции), привлекли новые возможности пространственных измерений, что на языке современных студий стало называться четвёртым измерением. Существуя в сознании образом пластики предмета, четвёртое измерение зарождается благодаря трём известным измерениям: оно представляет собой необъятность пространства во всех направлениях в каждый данный момент. Это само пространство, само измерение бесконечности; четвёртое измерение одаряет предметы пластичностью.
Поиском новых средств занимался сюрреалист Марсель Дюшан, хорошо знакомый с многомерной математикой и методами её визуализации. Среди наиболее характерных образцом его творчества — картины «Обнажённая на лестнице, № 2» и «Большое стекло». Аналогичные мотивы прослеживаются у футуристов, супрематистов («работы Малевича этого периода напоминают плоские сечения объектов из высших измерений») и сюрреалистов. У Сальвадора Дали есть картины «Распятие, или Гиперкубическое тело» и «В поисках четвёртого измерения»[8].
Примечания
- J. Scott Carter, Masahico Saito. Knotted Surfaces and Their Diagrams
- Стюарт, Иэн. Невероятные числа профессора Стюарта = Professor Stewart's incredible numbers. — М.: Альпина нон-фикшн, 2016. — С. 85—89. — 422 с. — ISBN 978-5-91671-530-9.
- Ибаньес, Рауль, 2014, с. 59—60, 71.
- Ибаньес, Рауль, 2014, с. 75—81..
- Владимиров Ю. С., 2010, с. 63—68.
- Ибаньес, Рауль, 2014, с. 87—102..
- Мир N измерений
- Ибаньес, Рауль, 2014, с. 133—155..
Литература
- Владимиров Ю. С. Пространство-время: явные и скрытые размерности. — Изд. 2-е, перераб. и доп. — М.: Книжный дом «ЛИБРОКОМ», 2010. — 208 с. — (Науку — всем! Шедевры научно-популярной литературы). — ISBN 978-5-397-01072-6.
- Ибаньес, Рауль. Четвёртое измерение. Является ли наш мир тенью другой Вселенной?. — М.: Де Агостини, 2014. — 160 с. — (Мир математики: в 45 томах, том 6). — ISBN 978-5-9774-0631-4.
Ссылки
- Dimensions — видео-прогулка по математическим размерностям, различные представления многомерных объектов, подробные примечания со ссылками (рус.)
- Покадровая анимация 4D—3D аналогий (англ.)
- Найти выход из лабиринта в 3Д и 4Д. Удобное управление на клавиатуре. Java (англ.) или для WinXP
- Jenn3D (англ.) — управляемый полет в 3-стереографической проекции 4-политопов, например, тессеракта
- 4D евклидово пространство (англ.)
- 4D Building Blocks — Interactive game to explore 4D space (англ.)
- 4DNav — Простой инструмент для просмотра 4-мерного объекта в четырёх 3-мерных проекциях (фр.) использует алгоритм прямолинейного проектирования ADSODA (англ.)
- Вики-сборник 4-мерия Гаррета Джонса (англ.)