Архимедово тело

Архиме́дово те́ло (или архиме́дов многогра́нник) — выпуклый многогранник, имеющий в качестве граней два или более типов правильных многоугольников, примыкающих к идентичным вершинам. Здесь «идентичные вершины» означают, что для любых двух вершин существует изометрия всего тела, переводящая одну вершину в другую.

Ромбоусечённый икосо­додекаэдр является самым большим архимедовым телом по объёму (для единичной длины ребра), а также имеющим больше всех других вершин и рёбер.
Псевдоромбокубооктаэдр имеет одну вершинную фигуру, 3.4.4.4, но с поворотом одного квадратного купола. В отличие от (не повёрнутого) ромбокубооктаэдра, фигура не является вершинно транзитивной.

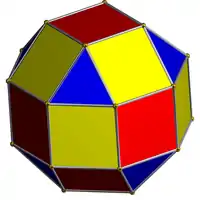
Архимедовы тела отличаются от платоновых тел (правильных многогранников), которые состоят только из одного типа многоугольников в одинаковых вершинах, и от многогранников Джонсона, правильные многоугольные грани которого принадлежат различным типам вершин.

Иногда только требуется, чтобы грани, прилегающие к одной вершине, были изометричными граням при другой вершине. Эта разница в определениях определяет, считается ли удлинённый квадратный гиробикупол (псевдо­ромбо­кубо­октаэдр) архимедовым телом или многогранником Джонсона — это единственный выпуклый многогранник, в котором многоугольные грани примыкают к вершине одним и тем же способом в каждой вершине, но многогранник не имеет глобальную симметрию, которая бы переводила любую вершину в любую другую. Основываясь на существовании псевдо­ромбо­кубо­октаэдра, Грюнбаум[1] предложил терминологическое различие, в котором архимедово тело определяется как имеющее одну и ту же вершинную фигуру в каждой вершине (включая удлинённый квадратный гиробикупол), в то время как однородный многогранник определяется как тело, у которого любая вершина симметрична любой другой (что исключает гиробикупол).

Призмы и антипризмы, группами симметрий которых являются диэдрические группы, обычно не считаются архимедовыми телами, несмотря на то, что они подпадают под определение, данное выше. С этим ограничением существует только конечное число архимедовых тел. Все тела, кроме удлинённого квадратного гирокупола, можно получить построениями Витхоффа из платоновых тел с помощью тетраэдральной, октаэдральной и икосаэдральной симметрий.

Источник названия

Архимедовы тела названы по имени Архимеда, обсуждавшего их в ныне потерянной работе. Папп ссылается на эту работу и утверждает, что Архимед перечислил 13 многогранников[1]. Во времена Возрождения художники и математики ценили чистые формы и переоткрыли их все. Эти исследования были почти полностью закончены около 1620 года Иоганном Кеплером[2], который определил понятия призм, антипризм и невыпуклых тел, известных как тела Кеплера — Пуансо.

Кеплер, возможно, нашёл также удлинённый квадратный гиробикупол (псевдоромбокубооктаэдр) — по меньшей мере, он утверждал, что имеется 14 архимедовых тел. Однако его опубликованные перечисления включают только 13 однородных многогранников, и первое ясное утверждение о существовании псевдоромбоикосаэдра было сделано в 1905 Дунканом Соммервилем[1].

Классификация

Существует 13 архимедовых тел (не считая удлинённого квадратного гиробикупола; 15, если учитывать зеркальные отражения двух энантиоморфов, которые ниже перечислены отдельно).

Здесь вершинная конфигурация относится к типам правильных многоугольников, которые примыкают к вершине. Например, вершинная конфигурация (4,6,8) означает, что квадрат, шестиугольник и восьмиугольник встречаются в вершине (порядок перечисления берётся по часовой стрелке относительно вершины).

Название
(Альтернативное название)		 Шлефли
Коксетер		 Прозрачный Непрозрачный Развёртка Вершинная
фигура		 Граней Рёбер Вершин Объём
(при единич-
ном ребре)		 Группа
точек
Усечённый тетраэдр{3,3}
(Вращение)		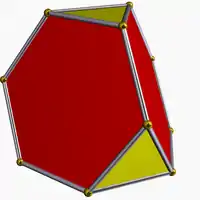 3.6.6
 8 4 треугольника
4 шестиугольника		 18 12 2.710576 Td
Кубооктаэдр
(ромботетраэдр)		r{4,3} или rr{3,3}
или
(Вращение)		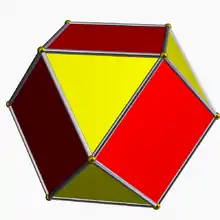 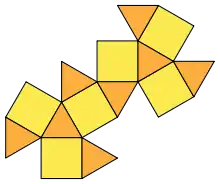3.4.3.4
 14 8 Треугольников
6 квадратов		 24 12 2.357023 Oh
Усечённый кубt{4,3}
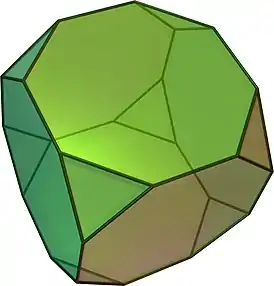(Вращение)		 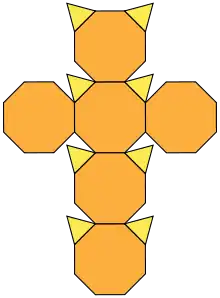3.8.8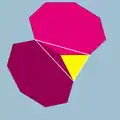
 14 8 треугольников
6 восьмиугольников		 36 24 13.599663 Oh
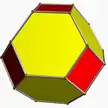
Усечённый октаэдр
(усечённый тетратераэдр)		t{3,4} или tr{3,3}
или

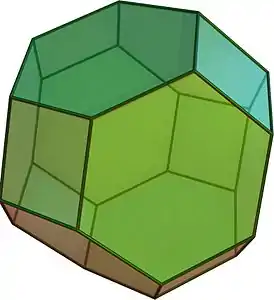(Вращение)

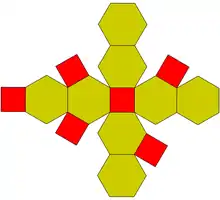 4.6.6
 14 6 квадратов
8 шестиугольников		 36 24 11.313709 Oh
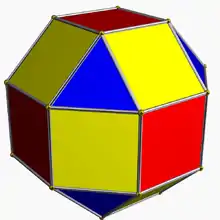
Ромбокубооктаэдр
(малый ромбокубооктаэдр)		rr{4,3}
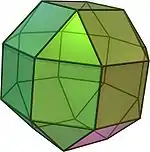(Вращение)		 3.4.4.4
 26 8 треугольников
18 квадратов		 48 24 8.714045 Oh
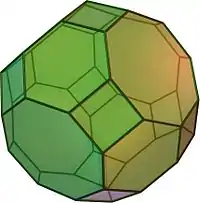
Усечённый кубооктаэдр
(большой ромбокубооктаэдр)		tr{4,3}
(Вращение)		 4.6.8
 26 12 квадратов
8 шестиугольников
6 восьмиугольников		 72 48 41.798990 Oh
Плосконосый куб
(плосконосый кубоктаэдр)		sr{4,3}
(Вращение)		 3.3.3.3.4
 38 32 треугольника
6 квадратов		 60 24 7.889295 O
Икосододекаэдрr{5,3}
(Вращение)		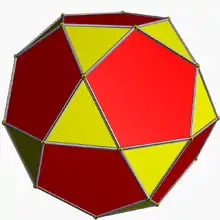 3.5.3.5
 32 20 треугольников
12 пятиугольников		 60 30 13.835526 Ih
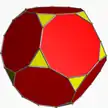
Усечённый додекаэдрt{5,3}
(Вращение)		 3.10.10
 32 20 треугольников
12 десятиугольников		 90 60 85.039665 Ih
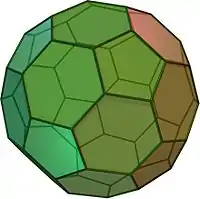
Усечённый икосаэдрt{3,5}
(Вращение)		 5.6.6
 32 12 пятиугольников
20 шестиугольников		 90 60 55.287731 Ih
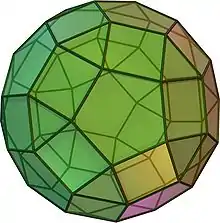
Ромбоикосододекаэдр
(малый ромбоикосододекаэдр)		rr{5,3}
(Вращение)		 3.4.5.4
 62 20 треугольников
30 квадратов
12 пятиугольников		 120 60 41.615324 Ih
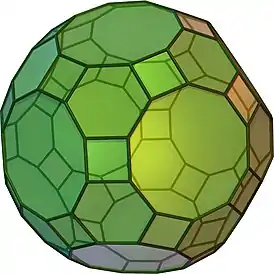
Ромбоусечённый икосододекаэдрtr{5,3}
(Вращение)		 4.6.10
 62 30 квадратов
20 шестиугольников
12 десятиугольников		 180 120 206.803399 Ih
Плосконосый додекаэдр
(плосконосый икосододекаэдр)		sr{5,3}
(Вращение)		 3.3.3.3.5
 92 80 треугольников
12 пятиугольников		 150 60 37.616650 I

Некоторые определения полуправильных многогранников включают ещё одно тело — удлинённый квадратный гиробикупол или «псевдоромбокубооктаэдр»[3].

Свойства

Число вершин равно отношению 720° к угловому дефекту при вершине.

Кубоктаэдр и икосододекаэдр являются рёберно однородными и называются квазиправильными.

Двойственные многогранники архимедовых тел называются каталановыми телами. Вместе с бипирамидами и трапецоэдрами они являются однородными по граням телами с правильными вершинами.

Хиральность

Плосконосый куб и плосконосый додекаэдр хиральны, поскольку они появляются в левостороннем и правостороннем вариантах. Если что-то имеет несколько видов, которые являются трёхмерным зеркальным отражением друг друга, эти формы называют энантиоморфами (это название применяется также для некоторых форм химических соединений).

Построение архимедовых тел
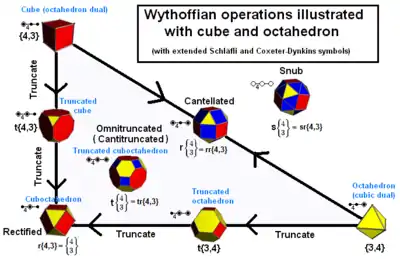
Архимедовы тела могут быть построены с помощью положения генератора в калейдоскопе

Различные архимедовы и платоновы тела могут быть получены друг из друга с помощью пригоршни операций. Начиная с платоновых тел можно использовать операцию усечения углов. Для сохранения симметрии усечение делается плоскостью, перпендикулярной прямой, соединяющей угол с центром многоугольника. В зависимости от того, насколько глубоко проводится усечение (см. таблицу ниже), получим различные платоновы и архимедовы (и другие) тела. Растяжение или скашивание осуществляется путём движения граней (в направлении) от центра (на одно и то же расстояние, чтобы сохранить симметрию) и созданием, затем, выпуклой оболочки. Расширение с поворотом осуществляется также вращением граней, это ломает прямоугольники, возникающие на местах рёбер, на треугольники. Последнее построение, которое мы здесь приводим, это усечение как углов, так и рёбер. Если игнорировать масштабирование, расширение можно также рассматривать как усечение углов и рёбер, но с определённым отношением между усечениями углов и рёбер.

Построение архимедовых тел
Симметрия Тетраэдральная
 Октаэдральная
Икосаэдральная
Начальное тело
Операция		Символ
{p, q}
 Тетраэдр
{3,3}
Куб
{4,3}
Октаэдр
{3,4}
Додекаэдр
{5,3}
Икосаэдр
{3,5}
Усечение (t)t{p, q}
 Усечённый тетраэдр
Усечённый куб
Усечённый октаэдр
Усечённый додекаэдр
Усечённый икосаэдр
Полное усечение (r)
Амвон (a)		r{p, q}
 Тетратетраэдр
Кубооктаэдр
Икосододекаэдр
Глубокое усечение (2t)
(dk)		2t{p, q}
 Усечённый тетраэдр
усечённый октаэдр
усечённый куб
усечённый икосаэдр
усечённый додекаэдр
Двойное полное усечение (2r)
Двойственный (d)		2r{p, q}
 тетраэдр
октаэдр
куб
икосаэдр
додекаэдр
Скашивание (rr)
Растяжение (e)		rr{p, q}
 Кубооктаэдр
Ромбокубооктаэдр
ромбоикосододекаэдр
Плосконосое спрямление (sr)
Спрямление (s)		sr{p, q}
 плосконосый тетратетраэдр
плосконосый куб
плосконосый икосододекаэдр
скос-усечение (tr)
Скашивание (b)		tr{p, q}
 Усечённый октаэдр
Усечённый кубооктаэдр
Ромбоусечённый икосододекаэдр

Заметим двойственность между кубом и октаэдром и между додекаэдром и икосаэдром. Также, частично вследствие самодвойственности тетраэдра, только одно архимедово тело имеет только одну тетраэдральную симметрию.

См. также

Примечания
  1. Grünbaum, 2009.
  2. Field, 1997, p. 241—289.
  3. Malkevitch, 1988, p. 85.

Литература
  • Field J.  Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler // Archive for History of Exact Sciences. — Springer, 1997. — Vol. 50, no. 3-4. — ISSN 0003-9519.
  • Grünbaum, Branko.  An enduring error // Elemente der Mathematik. — 2009. — Vol. 64, no. 3. — P. 89–101. — doi:10.4171/EM/120.. Перепечатано в The Best Writing on Mathematics 2010 / Mircea Pitici. — Princeton University Press, 2011. — P. 18–31.
  • Malkevitch, Joseph. . Shaping Space: A Polyhedral Approach / M. Senechal, G. Fleck. — Boston: Birkhäuser, 1988. — P. 80–92.
  • Pugh, Anthony. . Polyhedra: A visual approach. — California: University of California Press Berkeley, 1976. — ISBN 0-520-03056-7. Chapter 2
  • Udaya, Jayatilake.  Calculations on face and vertex regular polyhedral // Mathematical Gazette. — 2005. — Vol. 89, no. 514. — P. 76–81.
  • Williams, Robert. . The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc., 1979. — ISBN 0-486-23729-X. (Section 3-9)

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.