Скашивание (геометрия)

Скашивание — операция в пространстве любой размерности, при которой срезаются рёбра и вершины правильного многогранника, создавая новые грани на месте каждого ребра и вершины. Операцию можно применять к правильным мозаикам и сотам. Операция также является спрямлением полного усечения многогранника.

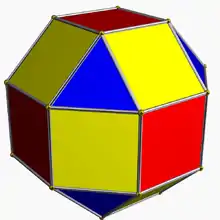
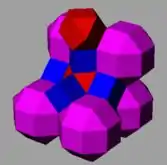
Скошенный куб — красные (исходные) грани куба уменьшились. Рёбра срезаны и образовали новые жёлтые грани. Вершины усечены с образованием синих треугольных граней.
Скошенные кубические соты — фиолетовые кубы скошены. Рёбра срезаны с образованием новых синих кубических ячеек. Вершины усечены с образованием новых красных спрямлённых кубических ячеек.

Операция (для многогранников и мозаик) также называется расширением (согласно Стотт), поскольку эту операцию можно представить как движение граней (в сторону удаления от центра многогранника), а на месте образовавшихся щелей образуются новые грани.

Обозначения

Операция представляется расширенным cимволом Шлефлиl t0,2{p,q,...}, или , или rr{p,q,...}.

Для многогранников операция скашивания даёт последовательность многогранников от правильного многогранника до его двойственного.

Пример последовательности от куба до октаэдра

Для многогранников больших размерностей скашивание даёт последовательность из правильного многогранника до его полного усечения. Кубооктаэдр можно рассматривать как полное усечение, например, тетраэдра.

Примеры многогранников и мозаик
Однородные многогранники и мозаики
Многогранники Мозаики
Коксетер rTT rCO rID rQQ rHΔ
Нотация
Конвея		 eT eC = eO eI = eD eQ eH = eΔ
Расширенные
многогранники		 Тетраэдр Куб или
Октаэдр		 Икосаэдр или
Додекаэдр		 Квадратная мозаика Шестиугольная мозаика
Треугольная мозаика
Рисунок
Вращающиеся
2-однородные многогранники
Коксетер rrt{2,3} rrs{2,6} rrCO rrID
Нотация
Конвея		 eP3 eA4 eaO = eaC eaI = eaD
Расширенные
многогранники		 Треугольная призма или
Треугольная бипирамида		 Квадратная антипризма или
Четырёхугольный трапецоэдр		 Кубооктаэдр или
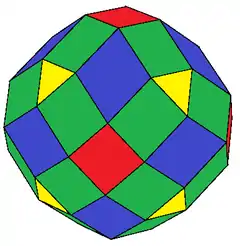
Ромбододекаэдр		 Икосододекаэдр или
Ромботриаконтаэдр
Рисунок
Вращающиеся

См. также

Литература
  • H.S.M. Coxeter. Chapter 8: Truncation, p. 210 Expansion // Regular Polytopes. — 3rd. — Dover edition, 1973. — P. 145—154. — ISBN 0-486-61480-8.
  • Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson : The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.