Дважды противоположно наращённый додекаэдр

Два́жды противополо́жно наращённый додека́эдр[1] — один из многогранников Джонсона (J59, по Залгаллеру — М3+М15+М3).

Дважды противоположно наращённый додекаэдр

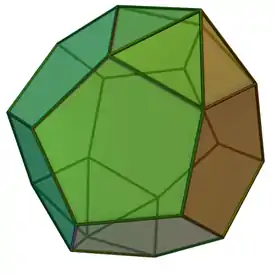(3D-модель)
Тип многогранник Джонсона
Свойства выпуклый
Комбинаторика
Элементы
20 граней
40 рёбер
22 вершины		 Χ = 2
Грани 10 треугольников
10 пятиугольников
Конфигурация вершины 10(53)
10(32.52)
2(35)
Развёртка
Классификация
Обозначения J59, М3+М15+М3
Группа симметрии D5d

Составлен из 20 граней: 10 правильных треугольников и 10 правильных пятиугольников. Каждая пятиугольная грань окружена четырьмя пятиугольными и треугольной; каждая треугольная грань окружена пятиугольной и двумя треугольными.

Имеет 40 рёбер одинаковой длины. 20 рёбер располагаются между двумя пятиугольными гранями, 10 рёбер — между пятиугольной и треугольной, остальные 10 — между двумя треугольными.

У дважды противоположно наращённого додекаэдра 22 вершины. В 10 вершинах сходятся три пятиугольных грани; в 10 вершинах сходятся две пятиугольных и две треугольных грани; в 2 вершинах сходятся пять треугольных граней.

Дважды противоположно наращённый додекаэдр можно получить из трёх многогранников — додекаэдра и двух пятиугольных пирамид (J2), — приложив основания пирамид к двум противоположным граням додекаэдра.

Метрические характеристики

Если дважды противоположно наращённый додекаэдр имеет ребро длины , его площадь поверхности и объём выражаются как

Примечания
  1. Залгаллер В. А. Выпуклые многогранники с правильными гранями / Зап. научн. сем. ЛОМИ, 1967. — Т. 2. — Cтр. 22.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.