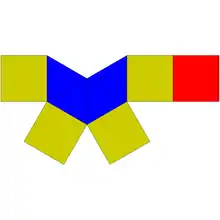
Удлинённая четырёхугольная пирамида

Если удлинённая четырёхугольная пирамида имеет ребро длины ${\displaystyle a}$, её площадь поверхности и объём выражаются как

${\displaystyle S=\left(5+{\sqrt {3}}\right)a^{2}\approx 6{,}7320508a^{2},}$

${\displaystyle V=\left(1+{\frac {\sqrt {2}}{6}}\right)a^{3}\approx 1{,}2357023a^{3}.}$

Удлинённую четырёхугольную пирамиду с длиной ребра ${\displaystyle 2}$ можно расположить в декартовой системе координат так, чтобы её вершины имели координаты

• ${\displaystyle (\pm 1;\;\pm 1;\;\pm 1),}$
• ${\displaystyle (0;\;0;\;1+{\sqrt {2}}).}$

При этом ось симметрии многогранника будет совпадать с осью Oz, а две из четырёх плоскостей симметрии — с плоскостями xOz и yOz.

С помощью удлинённых четырёхугольных пирамид и правильных тетраэдров можно замостить трёхмерное пространство без промежутков и наложений (см. иллюстрацию).

• Weisstein, Eric W. Удлинённая четырёхугольная пирамида (англ.) на сайте Wolfram MathWorld.