Усечённый кубооктаэдр

Граф усечённого кубооктаэдра
Граф усечённого кубооктаэдра
Вершин	48
Рёбер	72
Автоморфизмы	48
Хроматическое число	2
Свойства	кубический ; гамильтонов ; регулярный, ; нуль-симметричный
	Медиафайлы на Викискладе

Усечённый кубооктаэдр[1][2], усечённый кубоктаэдр[3] — полуправильный многогранник (архимедово тело) с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника, 48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию (что эквивалентно повороту на 180°), усечённый кубооктаэдр является зоноэдром.

Усечённый кубооктаэдр


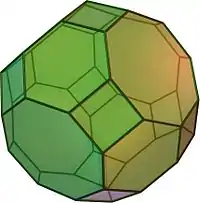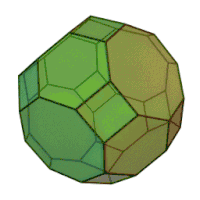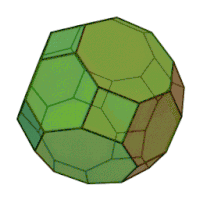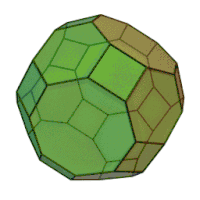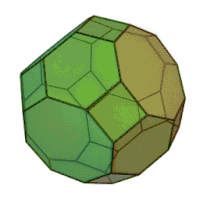Тип	Полуправильный многогранник
Грань	квадрат, шестиугольник, восьмиугольник
Граней	$26$
Рёбер	$72$
Вершин	$48$
Граней при вершине	$3$
Телесный угол	4-6:arccos(-sqrt(6)/3)=144°44’08" 4-8:arccos(-sqrt(2)/3)=135° 6-8:arccos(-sqrt(3)/3)=125°15’51"
Точечная группа симметрии	Октаэдрическая, [4,3]⁺, (432), порядок 24
Двойственный многогранник	Гекзакисоктаэдр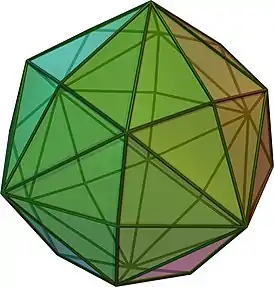
Развёртка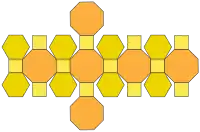
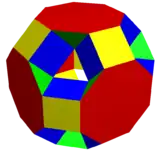
С раскраской граней	Вершинная фигура

Другие названия

Этот многогранник имеет несколько названий:

Усечённый кубооктаэдр (Иоганн Кеплер)
Ромбоусечённый кубооктаэдр (Магнус Веннинджер[4][5])
Большой ромбокубооктаэдр (Роберт Вильямс [6])
Большой ромбокубооктаэдр (Питер Кромвель [7])
Общеусечённый куб (omnitruncated cube) или скос-усечённый куб (cantitruncated cube) (Норман Джонсон)

Название усечённый кубооктаэдр, данное первоначально Иоганном Кеплером, несколько вводит в заблуждение. Усечение кубооктаэдра путём отсечения углов (вершин) не позволяет получить эту однородную фигуру — некоторые грани будут прямоугольниками. Однако полученная фигура топологически эквивалентна усечённому кубооктаэдру и всегда может быть деформирована до состояния, когда грани станут правильными.

Альтернативное название — большой ромбокубооктадр — ссылается на тот факт, что 12 квадратных граней лежат в тех же плоскостях, что и 12 граней ромбододекаэдра, который двойственен кубооктаэдру. Ср. малый ромбокубооктаэдр.

Также существует невыпуклый однородный многогранник с тем же именем — невыпуклый большой ромбокубооктаэдр.

Декартовы координаты

Декартовы координаты вершин усечённого кубооктаэдра, имеющего ребро длины 2 и имеющего центр в начале координат, являются перестановками чисел:

(±1, ±(1+√2), ±(1+2√2))

Площадь и объём

Площадь A и объём V усечённого кубооктаэдра с ребром длины a равны:

A=12\left(2+{\sqrt {2}}+{\sqrt {3}}\right)a^{2}\approx 61.7551724a^{2}

V=\left(22+14{\sqrt {2}}\right)a^{3}\approx 41.7989899a^{3}.

Рассечение

Усечённый кубооктаэдр можно препарировать (вырезать части), превратив его в центральный ромбокубооктаэдр с 6 квадратными куполами над первичными квадратными гранями, 8 треугольными куполами над треугольными гранями и 12 кубами над вторичными квадратными гранями.

Препарированный усечённый кубооктаэдр может дать тороиды Стюарта рода 5, 7 или 11, если удалить центральный ромбокубооктаэдр и либо квадратные купола, либо треугольные купола, или 12 кубов соответственно. Можно построить много других тороидов с меньшей степенью симметрии путём удаления подмножества этих компонент препарации. Например, удаление половины треугольных куполов создаёт тороид рода 3, который (при правильном выборе удаляемых куполов) имеет тетраэдральную симметрию[8][9].

Тороиды Стюарта
Род 3	Род 5	Род 7	Род 11

Однородные раскраски

Существует только одна однородная раскраска граней этого многогранника, по одному цвету на каждый тип грани.

Существует 2-однородная раскраска тетраэдральной симметрией с раскраской шестиугольников в два цвета.

Ортогональные проекции

Усечённый кубооктаэдр имеет две специальные ортогональные проекции в A₂ и B₂ плоскости Коксетера с [6] и [8] проективными симметриями, и множество [2] симметрий можно построить, исходя из различных плоскостей проекции.

Ортогональные проекции
Центрированы относительно	Вершины	Ребра 4-6	Ребра 4-8	Ребра 6-8	Нормали к грани 4-6
Изображение
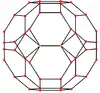Проективная симметрия	[2]⁺	[2]	[2]	[2]	[2]
Центрированы относительно	Нормали к квадрату	Нормали к восьмиграннику	Квадратной грани	Шестиугольной грани	Восьмиугольной грани
Изображение
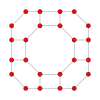Проективная симметрия	[2]	[2]	[2]	[6]	[8]

Сферические мозаики

Усечённый кубооктаэдр можно представить как сферическую мозаику и спроектировать на плоскость с помощью стереографической проекции. Эта проекция конформна, она сохраняет углы, но не сохраняет длины и площади. Прямые линии на сфере проецируются в круговые дуги на плоскости.

Ортогональная проекция	Стереографические проекции
	квадрат-центрированная	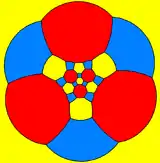шестиугольник-центрированная	восьмиугольник-центрированная

Связанные многогранники

Усечённый кубооктаэдр входит в семейство однородных многогранников, связанных с кубом и правильным октаэдром.

Однородные октаэдральные многогранники
Симметрия: [4,3], (*432)							[4,3]⁺, (432)	[3⁺,4], (3*2)


{4,3}	t{4,3}	r{4,3}	t{3,4}	{3,4}	rr{4,3}	tr{4,3}	sr{4,3}	s{3,4}
Двойственные многогранники

V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3⁵

Этот многогранник можно считать членом последовательности однородных вершинных фигур со схемой (4.6.2p) и диаграммой Коксетера — Дынкина . Для p < 6 члены последовательности являются общеусечёнными многогранниками (зоноэдрами), показанными ниже как сферические мозаики. Для p > 6 они являются мозаиками на гиперболической плоскости, начиная с усечённой трисемиугольной мозаики.

*n32 мутации по симметрии полностью усечённых мозаик: *4.6.2n*
Симметрия *n32 n,3	Сферическая				Евклидова	Компактная гиперболическая		Паракомп.	Некомпактная гиперболическая
Симметрия *n32 n,3	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Фигуры
Конфигурация	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Двойственная
Конфигурация грани	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

*n42 симметрии общеусечённых мозаик: *4.8.2n*
Симметрия *n42 [n,4]	Сферическая		Евклидова	Компактная гиперболическая				Паракомп.
Симметрия *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]…	*∞42 [∞,4]
Общеусечённая фигура	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Общеусечённые двойственные	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

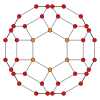
Граф усечённого кубооктаэдра

В теории графов граф усечённого кубооктаэдра (или граф большого ромбокубооктаэдра) — это граф вершин и рёбер усечённого кубооктаэдра. Он имеет 48 вершин и 72 ребра, нульсимметричен и является кубическим архимедовым графом [10].

Примечания

Веннинджер, 1974, с. 39.
Люстерник, 1956, с. 184.
Энциклопедия элементарной математики, 1963, с. 437, 434.
Веннинджер, 1974, с. 20, 39.
Wenninger, 1974, с. 29.
Williams, 1979, с. 82.
Cromwell, 1997, с. 82.
Stewart, 1970.
Adventures Among the Toroids — Chapter 5 — Simplest (R)(A)(Q)(T) Toroids of genus p=1
Read, Wilson, 1998, с. 269.

Литература

М. Веннинджер. Модели многогранников. — Мир, 1974.
Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М.: Государственное издательство физико-математической литературы, 1963. — С. 382—447.
Л. А. Люстерник. Выпуклые фигуры и многогранники. — М.: Государственное издательство технико-теоретической литературы, 1956.
Magnus Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — ISBN 978-0-521-09859-5. (Модель 15, стр. 29)
Robert Williams. The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc., 1979. — ISBN 0-486-23729-X.. (Секция 3-9, стр. 82)
P. Cromwell. Polyhedra. — United Kingdom: Cambridge, 1997. — С. 79–86 Archimedean solids. — ISBN 0-521-55432-2.
R.C. Read, R.J. Wilson. An Atlas of Graphs. — Oxford University Press, 1998.
B. M. Stewart. Adventures Among the Toroids. — 1970. — ISBN 978-0-686-11936-4.

Ссылки

Weisstein, Eric W. Great rhombicuboctahedral graph (англ.) на сайте Wolfram MathWorld.
3D convex uniform polyhedra
Editable printable net of a truncated cuboctahedron with interactive 3D view
The Uniform Polyhedra
Virtual Reality Polyhedra The Encyclopedia of Polyhedra
great Rhombicuboctahedron: paper strips for plaiting

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_75b3d5c94443edf0-1] Веннинджер, 1974, с. 39.

[_890f5fddf3101d53-2] Люстерник, 1956, с. 184.

[_4011b030f449b594-3] Энциклопедия элементарной математики, 1963, с. 437, 434.

[_df2c43b70bff23de-4] Веннинджер, 1974, с. 20, 39.

[_0f33af25959f6b00-5] Wenninger, 1974, с. 29.

[_a4b25bb2863c79ab-6] Williams, 1979, с. 82.

[_e06469bf5c08a1d0-7] Cromwell, 1997, с. 82.

[_7703484a773cfd20-8] Stewart, 1970.

[9] Adventures Among the Toroids — Chapter 5 — Simplest (R)(A)(Q)(T) Toroids of genus p=1

[_2a1fa18183c8a5e5-10] Read, Wilson, 1998, с. 269.