Гамильтонов граф

Гамильтонов граф — граф, содержащий гамильтонов цикл[1]. При этом гамильтоновым циклом является такой цикл (замкнутый путь), который проходит через каждую вершину данного графа ровно по одному разу[2]; то есть простой цикл, в который входят все вершины графа.

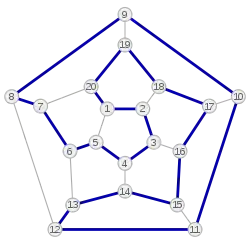
Гамильтонова линия для додекаэдра, предложенная Гамильтоном для замены его игры «вокруг света» на додекаэдре на задачу для плоского графа.

Также с гамильтоновым графом тесно связано понятие гамильтонова пути, который является простым путём (путём без петель), проходящим через каждую вершину графа ровно один раз[1]. Гамильтонов путь отличается от цикла тем, что у пути начальные и конечные точки могут не совпадать, в отличие от цикла. Гамильтонов цикл является гамильтоновым путём.

Гамильтоновы путь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру. В этой задаче вершины додекаэдра символизировали известные города, такие как Брюссель, Амстердам, Эдинбург, Пекин, Прага, Дели, Франкфурт и др., а рёбра — соединяющие их дороги. Путешествующий должен пройти «вокруг света», найдя путь, который проходит через все вершины ровно один раз[3]. Чтобы сделать задачу более интересной, порядок прохождения городов устанавливался заранее. А чтобы было легче запомнить, какие города уже соединены, в каждую вершину додекаэдра был вбит гвоздь, и проложенный путь отмечался небольшой верёвкой, которая могла обматываться вокруг гвоздя. Однако такая конструкция оказалась слишком громоздкой, и Гамильтон предложил новый вариант игры, заменив додекаэдр плоским графом, изоморфным графу, построенному на рёбрах додекаэдра[4].

Условия существования

Простое необходимое и достаточное условие существования гамильтонова цикла неизвестно[5].

Необходимое условие существования гамильтонова цикла в неориентированном графе: если неориентированный граф G содержит гамильтонов цикл, тогда в нём не существует ни одной вершины с локальной степенью . Доказательство следует из определения.

Условие Поша: Пусть граф G имеет вершин. Если для всякого , , число вершин со степенями меньшими или равными n меньше, чем n, и для нечетного число вершин со степенью не превосходит , то G — гамильтонов граф. Это достаточное условие не является необходимым[6].

Как следствие теоремы Поша, получаем более простые и менее сильные достаточные условия, найденные Дираком и Оре.

В 1952 году было сформулировано условие Дирака существования гамильтонова цикла: пусть  — число вершин в данном графе и ; если степень каждой вершины не меньше, чем , то данный граф — гамильтонов[7].

Основная статья: Теорема Оре

Условие Оре: пусть  — количество вершин в данном графе и . Если для любой пары несмежных вершин выполнено неравенство , то данный граф — гамильтонов (другими словами: сумма степеней любых двух несмежных вершин не меньше общего числа вершин в графе)[7].

Теорема Бонди — Хватала обобщает утверждения Дирака и Оре. Граф является гамильтоновым тогда и только тогда, когда его замыкание — гамильтонов граф. Для графа G с n вершинами замыкание строится добавлением в G ребра (u,v) для каждой пары несмежных вершин u и v, сумма степеней которых не меньше n[8].

Алгоритм поиска гамильтонова пути

Эвристические оптимизации

При прямом переборе вариантов вершин возможно значительное увеличение средней сложности поиска гамильтонова пути на случайных графах (если гарантируется наличие гамильтонова пути в графе). Для улучшения данного способа можно на каждом шаге перебора при некоторой построенной части цепи проверять, образуют ли оставшиеся вершины связный граф (если не образуют, то цепь не может являться началом гамильтоновой цепи); на каждом шаге перебора при выборе следующей вершины пробовать сначала вершины с наименьшей остаточной степенью (количеством рёбер, ведущих в ещё не посещённые вершины). Кроме того, если это дерево является цепью, то гамильтонов цикл в нём возможен. Иначе (если в дереве есть вершины со степенью не меньше, чем 3) построение гамильтонова цикла невозможно[9].

Примеры использования

Криптография

Гамильтонов цикл используется в системе так называемых протоколов с нулевым разглашением.

Пусть Пегги и Виктор знают один и тот же гамильтонов граф G, причём Пегги знает в нём гамильтонов цикл. Она хочет доказать это Виктору, не раскрывая ему самого цикла. Существует алгоритм того, как она должна действовать[10]:

1. Пегги случайным образом преобразовывает граф G. Передвигая точки и изменяя их метки, она создаёт новый граф H, топологически изоморфный G. Тогда, зная гамильтонов цикл в G, она легко найдет его в H. Если бы она не сама создавала H, то определение изоморфизма между графами было бы слишком сложной задачей, решение которой требует огромного количества времени. Затем она шифрует H и получает граф H'.

2. Пегги передаёт Виктору H'.

3. Виктор просит Пегги либо:

  1. Доказать, что H' — зашифрованная изоморфная копия G, либо
  2. Показать гамильтонов цикл для H.

4. Пегги выполняет его просьбу. Она либо:

  1. Доказывает, что H' — зашифрованная изоморфная копия G, раскрывая преобразования и всё расшифровывая, не показывая гамильтонов цикл для G или H, либо
  2. Показывает гамильтонов цикл для H, расшифровывая только то, что образует гамильтонов цикл, не доказывая, что H и G топологически изоморфны.

5. Пегги и Виктор повторяют этапы 1 — 4 n раз.

Если Пегги не обманывает, то она сможет рассказать Виктору любое из доказательств на этапе 3. Однако если гамильтонов цикл для G ей самой неизвестен, она не сможет создать H', удовлетворяющий обоим доказательствам. Правда, Пегги может создать или граф, изоморфный G, или граф с таким же числом вершин и рёбер и правильным гамильтоновым циклом. И, хотя с вероятностью 50 % она может угадать, какое доказательство попросит Виктор на этапе 3, Виктор может повторить протокол достаточное число раз, пока не убедится, что Пегги знает гамильтонов цикл в G.

Экстремальные задачи теории графов: Задача коммивояжёра
Основная статья: Задача коммивояжёра

Коммивояжёру необходимо посетить каждый город в пределах некоторой территории и возвратиться в пункт отправления. Требуется, чтобы путь был как можно короче. Таким образом, исходная задача преобразуется в задачу поиска минимальной протяженности (длительности или стоимости)[11].

Задачу можно переформировать в терминах теории графов — построить такой граф G(X, A), вершины которого соответствуют городам, а ребра — коммуникации между городами. Решение этой задачи ищут среди гамильтоновых циклов построенного графа.

Известно много способов решения этой задачи. Можно выделить методы, разработанные Беллмором и Немхаузером[12], Гарфинкелем и Немхаузером[13], Хелдом и Карпом[14], Стекханом[15]. Также известными решениями задачи коммивояжёра являются метод ветвей и границ и метод последовательного улучшения решения[16].

Связанные термины

Полугамильтоновым[17] графом называется граф, содержащий простую цепь, проходящую через каждую его вершину ровно один раз. При этом, всякий гамильтонов граф является полугамильтоновым. Гамильтонов цикл является простым остовным циклом[18].

Суть задачи о гамильтоновом цикле — выяснить, имеет ли заданный граф G гамильтонов цикл. Данная задача является NP-полной[19].

Гамильтонова орцепь орграфа[20] — простая цепь, проходящая через каждую вершину орграфа ровно один раз.

Гамильтоновым орциклом[20] называется орцикл[20] орграфа, который проходит через каждую его вершину.

Орграф называется полугамильтоновым[20], если он имеет гамильтонову орцепь, и гамильтоновым[20], если обладает гамильтоновым орциклом.

См. также

Примечания
  1. М. О. Асанов, В. А. Баранский, В. В. Расин. Дискретная математика: графы, матроиды, алгоритмы. — Ижевск: Регулярная и хаотическая динамика, 2001. — С. 41. — ISBN 5-93972-076-5.
  2. Свами, Тхуласираман, 1984, с. 55.
  3. Харари, 2003, с. 16—17.
  4. О. Оре. Графы и их применение. — Москва: Мир, 1965. — С. 40—41.
  5. Дмитрий Максимов. Пути и маршруты // Наука и жизнь. — 2020. — № 2. — С. 81—86.
  6. Харари, 2003, с. 86.
  7. Харари, 2003, с. 87.
  8. Свами, Тхуласираман, 1984, с. 61.
  9. Графы и алгоритмы: Лекция 8: Эйлеровы и гамильтоновы циклы. НОУ Интуит.
  10. Шнайер, 2002, с. 89—90.
  11. Майника, 1981, с. 241—264.
  12. Bellmore M., Nemhuser G. L. The Travelling Salesman Problem: A. Survey. — ORSA vol. 16, 1968. — С. 538-558.
  13. Garfinkel R., Namhauser G. L. Integer Programming. — New York: John Wiley, Inc., 1972. — С. 354-360.
  14. Held M., Karp R. The Travelling-Salesman Problem and Minimum Spanning Trees, Part II // Math. Programming. — 1971. — Vol. 1. — P. 6-25. — doi:10.1007/BF01584070.
  15. Steckhan H. A. Theorem on Symmetric Travelling Salesman Problems. — ORSA, vol. 18, 1970. — С. 1163-1167.
  16. Майника, 1981, с. 255—264.
  17. Уилсон И. Р., Эддиман А. М. Практическое введение в Паскаль. — Москва: Радио и связь, 1983. — С. 143.
  18. Татт, 1988.
  19. Т. Кормен, Ч. Лейзерсон, Р. Ривест. Алгоритмы. Построение и анализ. — Москва: МЦНМО, 2002. — С. 845—846.
  20. Долгих, Петренко, 2007.

Литература
  • Ф. Харари. Теория графов. — М.: УРСС, 2003. — ISBN 5-354-00301-6.
  • Б. Шнайер. Прикладная криптография. Протоколы, алгоритмы и исходные тексты на языке C. — Триумф, 2002.
  • К. Берж. Теория графов и её применение. — Москва: Издательство иностранной литературы, 1962.
  • Р. Уилсон. Введение в теорию графов. — Москва: Мир, 1977.
  • У. Татт. Теория графов. — Москва: Мир, 1988. — ISBN 5-03-001001-7.
  • Н. Кристофидес. Теория Графов. — Москва: Мир, 1978.
  • Б. А. Долгих, А. А. Петренко. Дискретная математика. — Москва: МГИУ, 2007. — С. 126—127. — ISBN 978-5-276-01103-5.
  • М. Свами, К. Тхуласираман. Графы, сети и алгоритмы. — Москва: Мир, 1984.
  • Э. Майника. Алгоритмы оптимизации на сетях и графах. — Москва: Мир, 1981.

Ссылки

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.