Разделённая квадратная мозаика
Разделённая квадратная мозаика (или тетракис-квадратная мозаика — это мозаика в евклидовой плоскости, которая строится из квадратной мозаики путём деления каждого квадрата на четыре равнобедренных прямоугольных треугольника с вершинами в центрах квадратов, в результате чего образуется бесконечная конфигурация прямых. Мозаика может быть также построена путём деления каждого квадрата решётки на два треугольника диагональю, при этом диагонали соседних квадратов имеют различное направление. Мозаику можно получить также путём наложения двух квадратных мозаик, одна из которых повёрнута на 45 градусов и её масштаб увеличен на √2.
| Разделённая квадратная мозаика | |
|---|---|
 | |
| Тип | Двойственная полуправильной мозаики |
| Диаграмма Коксетера — Дынкина |
|
| Список граней | треугольник 45-45-90 |
| Конфигурация граней | V4.8.8 |
| Группа симметрии | p4m, [4,4], *442 |
| Симметрии вращения | p4, [4,4]+, (442) |
| Двойственная мозаика | Усечённая квадратная мозаика |
| Свойства | гранетранзитивная |
Конвей называл мозаику kisquadrille, то есть квадропаркет, полученный операцией «kis»[1]. Операция «kis» добавляет точку в центр грани и рёбра от этой точки до вершин грани, разбивая тем самым грани квадратной мозаики на треугольники. Мозаику называют также решёткой «Юнион Джек», поскольку она напоминает британский национальный флаг с треугольниками, окружающими вершины порядка 8[2].
Мозаика обозначается как V4.8.8, поскольку каждая равнобедренная треугольная грань имеет два вида вершин — одну вершину с 4 окружающими треугольниками и две вершины с 8 треугольниками.
Двойственная мозаика
Мозаика является двойственной для усечённой квадратной мозаики, имеющей один квадрат и два восьмиугольника в каждой вершине[3].
Приложения
Фрагмент 5 × 9 разделённой квадратной мозаики используется в качестве игровой доски для малагасийской настольной игры «Фанорона». В этой игре камни укладываются на вершины мозаики, а ходы осуществляются вдоль рёбер, захватывая камни противника, пока такие камни есть. В этой игре вершины степени 4 и вершины степени 8 называются соответственно слабым пересечением и сильным пересечением. Различие видов вершин играет важную роль в стратегии игры[4]. Похожая доска используется в бразильской игре Адуго и для игры «Заяц и собаки».
Разделённая квадратная мозаика была использована в наборе памятных почтовых марок, выпущенных почтовой службой США в 1997 с различным узором на двух различных марках[5].
Эта мозаика также образует базис для широко используемых узоров «вертушка», «мельница» и «битая тарелка» в выстёгивании одеял[6][7][8].
Симметрия
Типы симметрии мозаики (по типам симметрий группы обоев:
- симметрия cmm; при раскраске в четыре цвета элементарная ячейка состоит из 8 треугольников, фундаментальная область состоит из 2 треугольников (1/2 для каждого цвета)
- симметрия p4g; тёмные и светлые треугольники, элементарная ячейка имеет 8 треугольников, фундаментальная область состоит из 1 треугольника (1/2 для каждого чёрного и белого)
- симметрия p4m; все треугольники имеют один цвет (белый) и чёрные рёбра, элементарная ячейка состоит из 2 треугольников, фундаментальная область (1/2)
Рёбра разделённой квадратной мозаики образуют симплициальную конфигурацию прямых, свойство, общее с треугольной мозаикой и разделённой ромбической мозаикой.
Эти прямые образуют оси симметрии группы отражений (группа обоев [4,4], (*442) или p4m), имеющей треугольники мозаики в качестве фундаментальной области. Эта группа изоморфна, но не совпадает с группой автоморфизмов мозаики, которая имеет дополнительные оси симметрии, разбивающие треугольники, и которая в качестве фундаментальной области имеет половины треугольников.
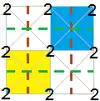
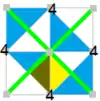
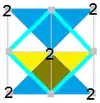
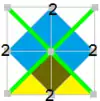
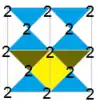
Имеется много групп подгрупп малых индексов p4m, (с симметрией [4,4], *442 в орбифолдной нотации), что можно видеть по диаграммам Коксетера — Дынкина с узлами, раскрашенными соответственно прямым отражения, а точки вращения помечены числами. Вращательная симметрия показана попеременными белыми и синими областями с одной фундаментальной областью для каждой подгруппы, показанной жёлтым. Скользящие симметрии даны пунктирными линиями.
Подгруппы можно выразить диаграммами Коксетера — Дынкина с их диаграммами фундаментальных областей.
| Подгруппы малых индексов p4m, [4,4], (*442) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Индекс | 1 | 2 | 4 | ||||||||
| Диаграмма фундаментальной области |
 |
 |
 |
 |
 |
 | |||||
| Нотация Коксетера Диаграмма Коксетера |
[1,4,1,4,1] = [4,4] |
[1+,4,4] |
[4,4,1+] |
[4,1+,4] |
[1+,4,4,1+] |
[4+,4+] = [(4,4+,2+)] | |||||
| Орбифолдная | *442 | *2222 | 22× | ||||||||
| Полупрямые подгруппы | |||||||||||
| Индекс | 2 | 4 | |||||||||
| Диаграмма | 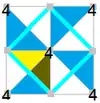 |
 |
 |
 |
 | ||||||
| Коксетер | [4,4+] |
[4+,4] |
[(4,4,2+)] |
[1+,4,1+,4]=[(2+,4,4)] |
[4,1+,4,1+]=[(4,4,2+)] | ||||||
| Орбифолдная | 4*2 | 2*22 | |||||||||
| Прямые подгруппы | |||||||||||
| Индекс | 2 | 4 | 8 | ||||||||
| Даиграмма | 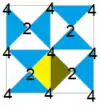 |
 |
 |
 |
 | ||||||
| Коксетер | [4,4]+ |
[1+,4,4+] = [4,4+]+ |
[4+,4,1+] = [4+,4]+ |
[(4,1+,4,2+)] = [(4,4,2+)]+ |
[1+,4,1+,4,1+] = [(4+,4+,2+)] = [4+,4+]+ | ||||||
| Орбифолдная | 442 | 2222 | |||||||||
Связанные многогранники и мозаики
Мозаика топологически связана с серией многогранников и мозаик с конфигурацией вершины Vn.6.6.
| Варианты симметрии *n42 усечённых мозаик: n.8.8 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *n42 [n,4] |
Сферическая | Евклидова | Компактная гиперболич. | Параком- пактная | |||||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | ||||
| Усечённые фигуры |
 |
 |
 |
 |
 |
 |
 |
 | |||
| Конфиг. | 2.8.8 | 3.8.8 | 4.8.8 | 5.8.8 | 6.8.8 | 7.8.8 | 8.8.8 | ∞.8.8 | |||
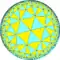
| n-kis фигуры |
 |
 |
 |
 |
 |
 |
 |
 | |||
| Конфиг. | V2.8.8 | V3.8.8 | V4.8.8 | V5.8.8 | V6.8.8 | V7.8.8 | V8.8.8 | V∞.8.8 | |||
| Симметрия *n42 [n,4] |
Сферическая | Евклидова | Компактная гиперболическая | Паракомп. | ||||
|---|---|---|---|---|---|---|---|---|
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]… |
*∞42 [∞,4] | |
| Общеусечённая фигура |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Общеусечённые двойственные |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
См. также
- Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
- Список однородных мозаик
- Порог протекания
Примечания
- Conway, Burgiel, Goodman-Strass, 2008.
- Stephenson, 1970.
- Weisstein, Eric W. Dual tessellation (англ.) на сайте Wolfram MathWorld.
- Bell, 1983, с. 150–151.
- Frederickson, 2006, с. 144.
- The Quilting Bible, 1997, с. 55.
- Zieman, 2011, с. 66.
- Fassett Kaffe, 2007, с. 96.
Литература
- Branko Grünbaum, G. C. Shephard. Tilings and Patterns. — W. H. Freeman, 1987. — С. 58—65 (Chapter 2.1: Regular and uniform tilings). — ISBN 0-7167-1193-1.
- Williams, R. The Geometrical Foundation of Natural Structure: A Source Book of Design. — New York: Dover Publications, 1979. — С. 40. — ISBN 0-486-23729-X.
- Keith Critchlow. Order in Space: A design source book. — New York: Thames & Hudson, 1987. — С. 77—76, pattern 8. — ISBN 0-500-34033-1.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table // The Symmetries of Things. — Wellesley, MA: A K Peters, Ltd., 2008. — ISBN 978-1-56881-220-5. Архивная копия от 19 сентября 2010 на Wayback Machine
- John Stephenson. Ising Model with Antiferromagnetic Next-Nearest-Neighbor Coupling: Spin Correlations and Disorder Points // Phys. Rev. B. — 1970. — Т. 1, вып. 11. — С. 4405—4409. — doi:10.1103/PhysRevB.1.4405.
- Bell R. C. Fanorona // The Boardgame Book. — Exeter Books, 1983. — С. 150—151. — ISBN 0-671-06030-9.
- Greg N. Frederickson. Piano-Hinged Dissections. — A K Peters, 2006. — ISBN 156881299X.
- The Quilting Bible. — Creative Publishing International, 1997. — ISBN 9780865732001.
- Nancy Zieman. Quilt With Confidence. — Krause Publications, 2011. — ISBN 9781440223556.
- Fassett Kaffe. Kaffe Fassett's Kaleidoscope of Quilts: Twenty Designs from Rowan for Patchwork and Quilting. — Taunton Press, 2007. — ISBN 9781561589388.
