Квадрирование квадрата

Квадри́рование квадра́та — задача о разбиении квадрата на конечное число меньших квадратов. В более узком смысле — задача о разбиении квадрата на конечное число попарно неравных между собой квадратов.

Разбиение квадрата на 21 квадрат, среди которых нет равных. Число внутри каждого квадрата означает длину его стороны. Соответственно, длина стороны большого квадрата равна (складывая длины сторон крайних квадратов) 50 + 35 + 27 = 50 + 29 + 33 = 33 + 37 + 42 = 27 + 19 + 24 + 42 = 112

В 1936—1938 годах её решили четверо студентов Тринити-колледжа Кембриджского университета[1].

Все квадраты в любом решении данной задачи имеют соизмеримые по длине стороны.[2]

Терминология
  • Квадрат, разбитый на попарно неравные квадраты, называется совершенным[1].
  • Порядком квадрата, разбитого на составные квадраты, называется число составляющих его квадратов.
  • Разбиение квадрата, никакое подмножество квадратов которого не образует прямоугольник (не считая отдельных квадратов), называется простым.

История
  • Вопрос о возможности разбиения квадрата на неравные квадраты был записан в Шотландской книге Станиславом Рузевичем под номером 59[3] в 1935-м году.
  • Самые первые найденные Бруксом, Смитом, Стоуном и Таттом совершенные квадраты были 69-го порядка.
  • В 1939 году Р. Шпраг (R. Sprague) нашёл совершенный квадрат 55-го порядка, это было первое опубликованное решение для совершенного квадрата[4].
  • Позднее Т. Г. Уиллкокс (T. H. Willcocks) нашёл совершенный квадрат 24-го порядка, который долгое время держал рекорд малости порядка.
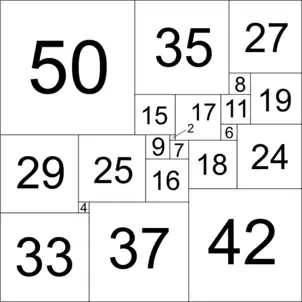
  • В 1978 году голландский математик А. Й. В. Дёйвестейн (A. J. W. Duijvestijn) с помощью компьютера нашёл разбиение квадрата на 21 квадрат, среди которых нет равных (см. рис.). Он также доказал следующие утверждения:
    • Не существует совершенного квадрата меньшего порядка.
    • Найденное им разбиение — единственно возможное для разбиения 21-го порядка.

Диаграмма Смита
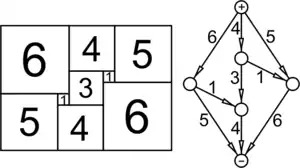
Диаграмма Смита для прямоугольника. Верхняя клемма «+» соответствует верхней стороне прямоугольника, нижняя клемма «−» — нижней стороне. Остальные клеммы соответствуют промежуточным горизонтальным отрезкам. Если длине стороны квадрата сопоставить силу тока, то диаграмма становится электрической схемой, для которой выполняются правила Кирхгофа. Например, длина верхней стороны прямоугольника складывается из сторон 6 + 4 + 5 = 15, что соответствует разветвлению тока в 15 единиц на три пропорциональные части.

Ключевую роль в решении задачи квадрирования сыграло предложение, сделанное Бруксом, Смитом, Стоуном и Татом в 1936—1938 годах[1] для анализа диаграммы, названной диаграммой Смита, которая любому разбиению квадрата (или прямоугольника) ставит в соответствие электрическую цепь. Это позволило применять для решения задачи квадрирования хорошо разработанную теорию электрических цепей.

Можно считать, что прямоугольник это проводник сделанный из фольги с постоянным удельным сопротивлением. Если вдоль оснований подключён ток, то сопротивление прямоугольника прямопропоционально высоте и обратно пропорционально ширине прямоугольника. Поэтому можно считать что сопротивление любого квадрата единица.

Каждому горизонтальному отрезку на схеме разбиения квадрата соответствует «клемма» этой цепи, а каждому квадрату разбиения — проводник, соединяющий две «клеммы». Сила тока, текущего по проводнику, равна длине стороны соответствующего квадрата. Поскольку можно считать, что сопротивление каждого квадрата равно единице, такая электрическая цепь ведёт себя как «настоящая»; в частности, подчиняется правилам Кирхгофа для токов в цепи.

Число квадрированных квадратов
Число простых совершенных
квадратов порядка 		Число простых совершенных
квадратов порядка
21 1 28 3001
22 8 29 7901
23 12 30 20 566
24 26 31 54 541
25 160 32 144 161
26 441 33 378 197[5]
27 1152

Число простых совершенных квадрированных квадратов порядка n с точностью до симметрий указано в последовательности A006983 в OEIS[6].

В 2013 году было найдено число квадратов порядка 32 (144 161)[6][5].

В июне 2014 года Джим Уильямс (Jim Williams) получил все 378 197 простых совершенных квадрированных квадратов порядка 33[5].

Кубирование куба

«Кубирование куба», то есть разбиение куба на конечное число попарно неравных между собой кубов, невозможно. Доказательство этого факта было дано Бруксом, Смитом, Стоуном и Таттом.

Доказательство

Допустим, что искомое разбиение куба существует.

Рассмотрим одну из граней куба, очевидно, не уменьшая общность, можно выбрать нижнюю грань.

На нижней грани стоят неравновеликие кубы, своими нижними рёбрами разбивающие грань на неравновеликие квадраты.

Найдём самый маленький квадрат разбиения нижней грани. Очевидно, что этот квадрат не может примыкать к ребру куба, будучи ограничен сторонами бо́льших квадратов, следовательно, он должен располагаться где-то внутри грани.

Теперь рассмотрим верхнюю грань этого малого кубика. Поскольку по предположению это самый маленький кубик на нижней грани куба, он окружен более высокими кубами. Поэтому на его верхнюю грань не заступает ни один соседний куб. Следовательно, стоящие на этой грани кубики меньшего размера снова разбивают верхнюю грань этого кубика на неравновеликие квадраты, причём самый малый квадрат разбиения верхней грани рассматриваемого кубика снова не может принадлежать ребру кубика и находится внутри грани.

Продолжая этот процесс рассуждения, приходим к противоречию, что доказывает теорему[1].

Гиперкубирование гиперкуба

Также легко доказывается теорема о невозможности «гиперкубирования гиперкуба» для гиперкубов любой размерности, большей 3-х. Действительно, для любой размерности n гиперкубы разбиения, прилегающие к какой-либо (n − 1)-мерной гиперграни исходного гиперкуба, должны разбивать эту гипергрань на конечное число попарно неравных (n − 1)-мерных гиперкубов. При n = 4 «гиперкубирование» невозможно, так как должно порождать «кубирование» 3-мерных гиперграней исходного 4-мерного гиперкуба. Индукцией по n можно сделать заключение о невозможности «гиперкубирования» для всех n > 3.

Ссылки

Литература
  • Гарднер М., Математические головоломки и развлечения. Пер. с английского Ю. Данилова. Изд. «Оникс», Москва, 1994, стр. 305—326.
  • Яглом И. М. Как разрезать квадрат серия «Математическая библиотечка» М., Наука, 1968—112 с.
  • Bouwkamp C. J., Duijvestijn A. J. W. Catalogue of Simple Perfect Squared Squares of Orders 21 Through 25, Eindhoven Univ. Technology, Dept. of Math., Report 92-WSK-03, Nov. 1992.
  • Bouwkamp C. J., Duijvestijn A. J. W. Album of Simple Perfect Squared Squares of order 26, Eindhoven University of Technology, Faculty of Mathematics and Computing Science, EUT Report 94-WSK-02, December 1994.
  • Brooks, R. L., Smith C. A. B., Stone, A. H., Tutte, W. T. The Dissection of Rectangles into Squares, Duke Math. J. 7, 312—340, 1940
  • Gardner Martin, Squaring the square, in The 2nd Scientific American Book of Mathematical Puzzles and Diversions.
  • Meschkowski H. Unsolved and Unsolvable Problems in Geometry, Oliver and Boyd, 1966, Edinburgh, pp. 9—102.
  • Stein S. Mathematics: The Man-Made Universe, (2nd ed.) Freeman and Co., 1969, San Francisco, pp. 92—124.
  • Tutte W. Squaring the Square, Canadian journal of Mathematics, 1950, pp.197—209.
  • Tutte W. The Quest of the Perfect Square, The American Mathematical Monthly, 1965, Vol. 72, No. 2, pp. 29—35.

Примечания
  1. Brooks, R. L.; Smith, C. A. B.; Stone, A. H.; and Tutte, W. T. The Dissection of Rectangles into Squares, Duke Math. J. 7, 312—340, 1940.
  2. Гарднер М., Математические головоломки и развлечения. Пер. с английского Ю. Данилова. Изд. «Оникс», Москва, 1994, стр. 305—326.
  3. The Scottish book (неопр.) / Stan Ulam. — 1958.
  4. 5. Towards a theory for combinatorial games. American Mathematical Society. Дата обращения: 30 июня 2017..
  5. Stuart Anderson. Simple Perfect Squared Squares (SPSSs); Order 21 to 33 and higher orders..
  6. Последовательность A006983 в OEIS = Number of simple perfect squared squares of order n up to symmetry.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.