Конфигурация прямых
Конфигура́ция прямы́х (или разбие́ние пло́скости прямы́ми)[1] — это разбиение плоскости, образованное набором прямых. Конфигурации прямых изучается в комбинаторной геометрии, а в вычислительной геометрии строятся алгоритмы для эффективного построения конфигураций.
Определение
Для любого множества A прямых на евклидовой плоскости можно определить отношение эквивалентности на точках плоскости, по которому две точки p и q эквивалентны, если для любой прямой l из A либо p и q обе лежат на прямой l, либо они лежат в той же самой открытой полуплоскости, ограниченной прямой l. Если A конечна или локально конечна[2], классы эквивалентности этих отношений принадлежат трём группам:
- внутренности ограниченных или неограниченных выпуклых многоугольников (ячейки разбиения), связные компоненты подмножества точек плоскости, не содержащихся ни на какой из прямых из A,
- открытые отрезки и открытые бесконечные лучи (рёбра разбиения), связные компоненты точек отдельной прямой, не принадлежащие никакой другой прямой из A,
- отдельные точки (вершины разбиения), пересечение двух или более прямых из A.
Эти три типа объектов, соединённые вместе, образуют клеточное разбиение, покрывающее плоскость. Говорят, что две конфигурации прямых изоморфны или комбинаторно эквивалентны, если существует один-в-один сохраняющее смежность соответствие между объектами в клеточных разбиениях[3]
Сложность наборов
Изучение конфигураций прямых начал Якоб Штейнер, доказавший первую границу максимального числа элементов разного типа, которое может содержать конфигурация[4][5]. Конфигурация из n прямых имеет не более n(n − 1)/2 вершин, по одной на пару пересекающихся вершин. Этот максимум достигается на простых конфигурациях. Конфигурация называется простой, если
- 1. никакие три прямые не пересекаются в одной точке
- 2. никакие две прямые не параллельны.
В любой конфигурации будет n бесконечных, направленных вниз лучей, по одному на прямую. Эти лучи отделяют n + 1 ячеек разбиения, неограниченных снизу. Все оставшиеся ячейки имеют единственную самую нижнюю вершину,[6] и каждая такая вершина является нижней для единственной ячейки, так что число ячеек разбиения равно числу вершин плюс n + 1 или не превосходит n(n + 1)/2 + 1, см. центральные многоугольные числа. Число рёбер разбиения не превосходит n2, что можно видеть либо с помощью эйлеровой характеристики, подставив число вершин и ячеек, либо используя наблюдение, что каждая прямая разделена максимум на n рёбер другими n − 1 прямыми. Снова, худшим случаем, на котором граница достигается, являются простые конфигурации прямых.
Зона прямой l в наборе прямых — это набор ячеек, имеющих рёбра, лежащие на l. Теорема о зоне утверждает, что полное число рёбер в ячейках отдельной зоны линейно. Точнее, полное число рёбер ячеек (из зоны прямой), находящихся по одной стороне прямой l, не больше 5n − 1[7][8][9], а полное число рёбер ячеек, лежащих по обе стороны от l, не превосходит [10]. Более обще, полная сложность ячеек разбиения, которые пересекаются выпуклой кривой, равна O(n α(n)), где α обозначает обратную функцию Аккермана, что можно показать, исходя из последовательностей Дэвенпорта–Шинцеля[10]. Суммируя сложность всех зон, можно обнаружить, что сумма квадратов сложностей ячеек в разбиении равна O(n2)[11].
k-уровень конфигурации прямых — это ломаная, образованная рёбрами, которые имеют в точности k других прямых под ней (то есть луч, опущенный вниз от ребра, пересекает в точности k прямых), а ≤k-уровень — это все части конфигурации прямых, находящиеся под k-уровнем. Нахождение верхней и нижней границ сложности для k-уровней остаётся главной открытой проблемой дискретной геометрии. Лучшей верхней границей является O(nk1/3), в то время как лучшей нижней — Ω(n exp(c (logk)1/2))[12][13][14]. Известно, что максимальная сложность ≤k-уровня равна Θ(nk)[15]. k-уровень является специальным случаем монотонного пути в разбиении плоскости, то есть последовательности рёбер, пересекающих любую вертикальную прямую в отдельной точке. Однако монотонные пути могут быть сложнее, чем k-уровни — существуют наборы прямых и монотонные пути в этих наборах, где число точек, на которых путь меняет направление, равно Ω(n2 − o(1))[16][17].
Хотя отдельная ячейка в разбиении может быть ограничена всеми n прямыми, невозможно в общем случае, чтобы m различных ячеек были ограничены n прямыми. Наоборот, полная сложность m ячеек почти равна Θ(m2/3n2/3 + n)[18][19] и почти та же самая граница появляется в теореме Семереди–Троттера об инциденции точек и прямых на плоскости. Простое доказательство этого факта следует из неравенства числа пересечений — если m ячеек имеют в общем счёте x + n рёбер, можно создать граф с m вершинами (по одной на ячейку) и x рёбрами (по одному на пару последовательных ячеек на той же самой прямой)[20][21]. Рёбра этого графа можно нарисовать как кривые, которые не пересекаются внутри ячеек, соответствующих конечным вершинам рёбер, а затем следуют по прямым набора. Таким образом, имеется O(n2) пересечений на этом рисунке. Однако, по неравенству числа пересечений, существует Ω(x3/m2) пересечений. Чтобы выполнялись оба неравенства, x должен быть O(m2/3n2/3)[22].
Проективные конфигурации и проективная двойственность
Часто удобно изучать конфигурацию прямых не в евклидовом пространстве, а на проективной плоскости, поскольку в проективной геометрии любая пара прямых имеет точку пересечения. На проективной плоскости мы не можем определить разбиение с использованием сторон прямых (прямая на проективной плоскости не разделяет плоскость на две различные стороны), но мы, всё же, можем определить ячейки разбиения как связные компоненты точек, не лежащих ни на какой прямой. Рёбрами будут связные компоненты, состоящие из множеств точек, принадлежащих отдельной прямой, а вершинами будут точки, где две или больше прямых пересекаются. Набор прямых на проективной плоскости отличается от его евклидового двойника, поскольку два евклидовых луча по обеим сторонам прямой заменяются одним ребром на проективной плоскости, а пары неограниченных евклидовых ячеек заменяются на проективной плоскости в единые ячейки.
Ввиду проективной двойственности многие утверждения о комбинаторных свойствах точек на плоскости могут быть более просто поняты в эквивалентной двойственной форме о конфигурациях прямых. Например, теорема Сильвестра, утверждающая, что любое неколлинеарное множество точек на плоскости имеет простую прямую, содержащая ровно две точки, превращается по проективной двойственности в утверждение, что любая конфигурация прямых, имеющая более одной вершины, имеет простую точку, вершину, в которой пересекаются всего две прямые. Наиболее раннее известное доказательство теоремы Сильвестра Мельхиором (Melchior (1940)) использует эйлерову характеристику.
Треугольники в наборах прямых
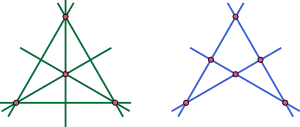
Говорят, что конфигурация прямых в проективной плоскости является симплициальной, если любая ячейка разбиения ограничена в точности тремя рёбрами. Симплициальные конфигурации первым изучал Мельхиор[23][24]. Три бесконечных семейства симплициальных наборов прямых известны:
- Почти-пучок состоит из n − 1 прямых, проходящих через одну точку, и одной прямой, которая через эту точку не проходит,
- Семейство прямых, образованных сторонами правильного многоугольника вместе с осями симметрии
- Стороны и оси симметрии чётного правильного многоугольника, вместе с прямой на бесконечности.
Кроме того, имеется много других примеров единичных симплициальных конфигураций, которые не вмещаются в какое-либо известное бесконечное семейство[25][24]. Как пишет Грюнбаум[24], симплициальные наборы прямых «появляются в качестве примеров или контрпримеров во многих контекстах комбинаторной геометрии и её приложений». Например, Артье, Грюнбаум и Ллибре[26] использовали симплициальные наборы прямых для построения контрпримеров гипотезе о связи между степенями набора дифференциальных уравнений и числом инвариантных прямых, которые уравнения могут иметь. Два известных контрпримера гипотезе Дирака-Моцкина (которая утверждает, что любая конфигурация n прямых имеет по меньшей мере n/2 простых точек) оба симплициальны[27][28][29][30].
Двойственным графом конфигурации прямых, в которой существует одна вершина для ячейки и одно ребро, соединяющее вершины, соответствующие ячейкам с общим ребром в конфигурации, является частичный куб, граф, в котором вершины можно пометить битовыми векторами таким образом, что расстояние на графе равно расстоянию Хэмминга между метками. В случае конфигураций прямых каждая координата принимает значение 0 для рёбер с одной стороны прямой и 1 для рёбер с другой стороны[31]. Двойственные графы симплициальных конфигураций использовались для построения бесконечных семейств 3-регулярных частичных кубов, изоморфных графам простого зоноэдра[32].
Интересно также изучить экстремальные количества треугольных ячеек в конфигурации, которая не обязательно симплициальна. В любой конфигурации должно быть по меньшей мере n треугольников. Любая конфигурация, имеющая только n треугольников, должна быть простой[25][33][34]. Известно, что максимальное возможное число треугольников в простой конфигурации ограничена сверху числом n(n − 1)/3, а минимальная граница равна n(n − 3)/3. Нижняя граница достигается на некоторых подмножествах диагоналей правильного 2n-угольника[35][25]. Для непростых конфигураций максимальное число треугольников похоже, но более сильно ограничено[36][37][38]. Тесно связанная задача Кобона о треугольниках спрашивает о максимальном числе неперекрывающихся конечных треугольников (не обязательно граней) в конфигурации на евклидовой плоскости. Для некоторых, но не для всех значений n, возможно n(n − 2)/3 треугольников.
Мультисеточные мозаики и мозаики Пенроуза

Двойственный граф простой конфигурации прямых можно представить геометрически как набор ромбов, по одному на вершину конфигурации со сторонами, перпендикулярными прямым, которые пересекаются в вершине. Эти ромбы могут быть объединены с образованием замощения выпуклого многоугольника в случае конфигурации конечного числа прямых или всей плоскости в случае локально конечных конфигураций с бесконечным числом прямых. Де Брёйн[39] исследовал специальные случаи этого построения, в которых конфигурация прямых состоит из k множеств параллельных прямых с равным отстоянием друг от друга. Для двух перпендикулярных семейств параллельных прямых это построение просто даёт знакомый квадратный паркет на плоскости, а для трёх семейств прямых под углом 120 градусов по отношению друг к другу (тем самым формирующие тришестиугольную мозаику) построение даёт ромбическую мозаику. Однако для большего числа семейств прямых это построение даёт апериодичные мозаики. В частности, для пяти семейств прямых с равными углами друг к другу (или, как де Брёйн называет эту конфигурацию, пентагрида) это даёт семейство замощений, которое включает ромбическую версию мозаик Пенроуза.
Разделённая квадратная мозаика — это бесконечная конфигурация прямых, образующая периодическое замощение, которое напоминает мультисетку с четырьмя параллельными семействами, но в которой два семейства имеют большее расстояние между прямыми, чем в других двух, и в которых набор прямых является симплициальным, а не простым. Двойственной мозаикой является усечённая квадратная мозаика. Подобным образом, треугольный паркет является бесконечной симплициальной конфигурацией прямых с тремя семействами параллельных прямых, у которой двойственной мозаикой является шестиугольный паркет, а разделённая шестиугольная мозаика является бесконечной симплициальной конфигурацией прямых с шестью семействами параллельных прямых и двумя расстояниями между прямыми в семействах, которая двойственна большой ромбитришестиугольной мозаике.
Алгоритмы
Конструирование конфигурации означает вычисление представления вершин, рёбер и ячеек конфигурации прямых (вместе с их взаимосвязями) при задании списка прямых в наборе, например как в двусвязном списке рёбер. Согласно теореме о зонах, наборы можно построить эффективно с помощью инкрементного алгоритма, который добавляет по одной прямой за шаг к набору прямых, добавленных на предыдущих шагах — каждая новая прямая может быть добавлена за время, пропорциональное её зоне, что в результате даёт время O(n2)[7]. Однако требования к памяти в этом алгоритме высоки, так что может быть более удобным перечисление всех свойств конфигурации в алгоритме, не сохраняющем всю конфигурации в памяти. Это можно сделать эффективно за время O(n2) и с памятью O(n) с помощью алгоритмической техники, известной как топологическое выметание[40]. Точное вычисление конфигурации прямых требует вычислительную точность, в несколько раз большую, чем входные данные (координаты) — если прямая задаётся двумя точками на ней, координаты конфигурации вершин могут потребовать в четыре раза большую точность, чем точность точек входных данных. Поэтому в вычислительной геометрии изучают также алгоритмы построения конфигураций эффективно с ограниченной численной точностью[41][42][43].
Также исследователи изучали эффективные алгоритмы построения меньших частей конфигурации, таких как зоны[44], k-уровни[45][46][47][48] или множества ячеек, содержащих заданный набор точек[49][50][51]. Задача нахождения конфигурации вершин с медианой x-координат возникает (в двойственной форме) в робастных статистиках как задача вычисления оценки Тейла — Сена множества точек[52].
Марк ван Кревельд предложил алгоритмическую задачу вычисления кратчайшего пути между вершинами в конфигурации прямых, где пути ограничены рёбрам конфигурации. Задача ставится так: есть ли алгоритмы, работающие за время, меньшее чем квадратичное, которое потратил бы алгоритм поиска кратчайшего пути в полном графе конфигурации[53]. Известен аппроксимационный алгоритм[54], и задача может быть эффективно решена для прямых, которые разбиваются на небольшое число семейств параллельных прямых (что типично для улиц городов)[55], однако задача в общем виде остаётся открытой.
Вариации и обобщения
Конфигурация псевдопрямых
Конфигурация псевдопрямых — это конфигурация кривых, имеющих похожие топологические свойства с конфигурацией прямых[25][56]. Их наиболее просто можно определить на проективной плоскости как простые замкнутые кривые, из которых любые две пересекаются трансверсально в единственной точке. Говорят, что конфигурация псевдопрямых растяжима, если онa комбинаторно эквивалентен конфигурации прямых. Задача отличения выпрямляемых наборов от невыпрямляемых[57][58] является NP-полной. Любая конфигурация конечного числа псевдопрямых может быть расширена, так что псевдопрямые становятся прямыми в неевклидовой геометрии инцидентности, в которой любые две точки топологической плоскости соединены единственной прямой (как на евклидовой плоскости), но в которой другие аксиомы евклидовой геометрии могут не выполняться.
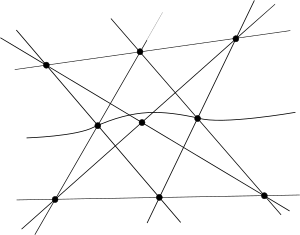 Нерастяжимый набор девяти псевдопрямых. (Все наборы с числом псевдопрямых меньше девяти выпрямляемы.) По теореме Паппа эта конфигурация не может быть реализована в проективной плоскости над любым полем. |
 Гиперболическая конфигурация прямых комбинаторно эквивалентна диаграмме хорд, использованной Агеевым[59] для доказательства, что круговой граф без треугольников может иногда требовать пять цветов. |
Плоскость Лобачевского
Другим типом неевклидовой геометрии является плоскость Лобачевского, и конфигурации гиперболических прямых в этой геометрии также изучались. Любое конечное множество прямых на евклидовой плоскости имеет комбинаторно эквивалентную конфигурацию в гиперболической плоскости (например, заключая вершины набора в большой круг и интерпретируя внутренность цикла как модель Клейна гиперболической плоскости). Однако в гиперболическом наборе прямых можно избежать пересечения прямых без требования параллельности прямых. Граф пересечений прямых в гиперболической конфигурации является круговым графом. Соответствующее понятие гиперболической конфигурации прямых для псевдопрямых — слабая конфигурация псевдопрямых[60], семейство кривых, имеющее те же топологические свойства, что и прямые[61], такие, что любые две кривые в семействе либо пересекаются в одной точке, либо не пересекаются вообще.
См. также
- Конфигурация, набор прямых и множество точек, в котором все прямые содержат одно и то же число точек, а все точки принадлежат одному и тому же числу прямых.
- Конфигурация (разбиение пространства), разбиение плоскости, заданной кривыми, или пространств больших размерностей, заданных поверхностями, когда не требуется, чтобы поверхность была плоскостью.
Примечания
- В англоязычной литературе аrrangement, что часто переводится как конфигура́ция, однако существует другой термин configuration, который естественно переводить тоже словом конфигура́ция. Иногда используется термин набо́р прямы́х, иногда — разбие́ние (прямыми или гиперплоскостями).
- В локально конечных наборах любое ограниченное подмножество плоскости может пересекаться лишь конечным числом прямых.
- Grünbaum, 1972, с. 4.
- Steiner, 1826.
- Agarwal, Sharir, 2000.
- Для ячеек, в которых имеется горизонтальное нижнее ребро, выбираем вершину справа.
- Chazelle et al, 1985.
- Edelsbrunner, 1987.
- Edelsbrunner, O'Rourke, Seidel, 1986.
- Bern, Eppstein, Plassman, Yao, 1991.
- Aronov, Matoušek, Sharir, 1994.
- Dey, 1998.
- Tóth, 2001.
- Задачу ограничения сложности k-уровней впервые изучали Ловаш (Lovász (1971)) и группой Эрдёш, Симонс, Страус (Erdős et al (1973)).
- Alon, Győri, 1986.
- Balogh et el, 2004.
- Matoušek, 1991.
- Canham, 1969.
- Clarkson et al, 1990.
- Ajtai, Chvátal, Newborn, Szemerédi, 1982.
- Leighton, 1983.
- Székely, 1997.
- Melchior, 1940.
- Grünbaum, 2005.
- Grünbaum, 1972.
- Artés, Grünbaum, Llibre, 1998.
- Crowe, McKee, 1968.
- Dirac, 1951.
- Kelly, Moser, 1958.
- Grünbaum, 1972, с. 18.
- Eppstein, Falmagne, Ovchinnikov, 2007.
- Eppstein, 2006.
- Levi, 1926.
- Roudneff, 1988.
- Füredi, Palásti, 1984.
- Purdy, 1979.
- Purdy, 1980.
- Strommer, 1977.
- de Bruijn, 1981.
- Edelsbrunner, Guibas, 1989.
- Fortune, Milenkovic, 1991.
- Greene, Yao, 1986.
- Milenkovic, 1989.
- Aharoni et al, 1999.
- Agarwal, de Berg, Matoušek, Schwarzkopf, 1998.
- Chan, 1999.
- Cole, Sharir, Yap, 1987.
- Edelsbrunner, Welzl, 1986.
- Agarwal, 1990.
- Agarwal, Matoušek, Sharir, 1998.
- Edelsbrunner, Guibas, Sharir, 1990.
- Cole, Salowe, Steiger, Szemerédi, 1989.
- Erickson, 1997.
- Bose et al, 1996.
- Eppstein, Hart, 1999.
- Agarwal, Sharir, 2002.
- Shor, 1991.
- Schaefer, 2010.
- Ageev, 1996.
- de Fraysseix, Ossona de Mendez, 2003.
- Альтернативное определение Шора Shor (1991) — псевдопрямая является образом прямой гомеоморфизма плоскости.
Литература
- P. K. Agarwal. Partitioning arrangements of lines II: Applications // Discrete and Computational Geometry. — 1990. — Т. 5, вып. 1. — С. 533–573. — doi:10.1007/BF02187809.
- P. K. Agarwal, M. de Berg, J. Matoušek, O. Schwarzkopf. Constructing levels in arrangements and higher order Voronoi diagrams // SIAM Journal on Computing. — 1998. — Т. 27, вып. 3. — С. 654–667. — doi:10.1137/S0097539795281840.
- P. K. Agarwal, J. Matoušek, M. Sharir. Computing many faces in arrangements of lines and segments // SIAM Journal on Computing. — 1998. — Т. 27, вып. 2. — С. 491–505. — doi:10.1137/S009753979426616X.
- P. K. Agarwal, M. Sharir. Handbook of Computational Geometry. — Elsevier, 2000. — С. 49–119.
- P. K. Agarwal, M. Sharir. Proc. 13th ACM-SIAM Symp. Discrete algorithms (SODA '02). — San Francisco: Society for Industrial and Applied Mathematics, 2002. — С. 800–809.
- A. A. Ageev. A triangle-free circle graph with chromatic number 5 // Discrete Math.. — 1996. — Т. 152. — С. 295–298. — doi:10.1016/0012-365X(95)00349-2.
- Y. Aharoni, D. Halperin, I. Hanniel, S. Har-Peled, C. Linhart. Proc. 3rd Int. Worksh. Algorithm Engineering (WAE '99). — Springer-Verlag, 1999. — Т. 1668. — С. 139–153. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-48318-7_13.
- M. Ajtai, V. Chvátal, M. Newborn, E. Szemerédi. Theory and Practice of Combinatorics. — North-Holland, 1982. — Т. 60. — С. 9–12. — (North-Holland Mathematics Studies).
- N. Alon, E. Győri. The number of small semi-spaces of a finite set of points in the plane // Journal of Combinatorial Theory, Series A. — 1986. — Т. 41. — С. 154–157. — doi:10.1016/0097-3165(86)90122-6.
- B. Aronov, J. Matoušek, M. Sharir. On the sum of squares of cell complexities in hyperplane arrangements // Journal of Combinatorial Theory, Series A. — 1994. — Т. 65, вып. 2. — С. 311–321. — doi:10.1016/0097-3165(94)90027-2.
- J. C. Artés, B. Grünbaum, J. Llibre. On the number of invariant straight lines for polynomial differential systems // Pacific Journal of Mathematics. — 1998. — Т. 184, вып. 2. — С. 207–230. — doi:10.2140/pjm.1998.184.207.
- J. Balogh, O. Regev, C. Smyth, W. Steiger, M. Szegedy. Long monotone paths in line arrangements // Discrete and Computational Geometry. — 2004. — Т. 32, вып. 2. — С. 167–176. — doi:10.1007/s00454-004-1119-1.
- M. W. Bern, D. Eppstein, P. E. Plassman, F. F. Yao. Discrete and Computational Geometry: Papers from the DIMACS Special Year / J. E. Goodman, R. Pollack, W. Steiger. — Amer. Math. Soc., 1991. — С. 45–66. — (DIMACS Ser. Discrete Math. and Theoretical Computer Science).
- P. Bose, W. Evans, D. G. Kirkpatrick, M. McAllister, J. Snoeyink. Proc. 8th Canadian Conf. Computational Geometry. — 1996. — С. 143–148.
- N. G. de Bruijn. Algebraic theory of Penrose's non-periodic tilings of the plane. — Indagationes Mathematicae. — 1981. — Т. 43. — С. 38–66.
- R. Canham. A theorem on arrangements of lines in the plane // Israel J. Math.. — 1969. — Т. 7, вып. 4. — С. 393–397. — doi:10.1007/BF02788872.
- T. Chan. Remarks on k-level algorithms in the plane. — 1999.
- B. Chazelle, L. J. Guibas, D. T. Lee. The power of geometric duality // BIT. — 1985. — Т. 25, вып. 1. — С. 76–90. — doi:10.1007/BF01934990.
- K. Clarkson, H. Edelsbrunner, L. J. Guibas, M. Sharir, E. Welzl. Combinatorial complexity bounds for arrangements of curves and spheres. — Discrete and Computational Geometry. — 1990. — Т. 5. — С. 99–160. — doi:10.1007/BF02187783.
- Richard Cole, Jeffrey S. Salowe, W. L. Steiger, Endre Szemerédi. An optimal-time algorithm for slope selection // SIAM Journal on Computing. — 1989. — Т. 18, вып. 4. — С. 792–810. — doi:10.1137/0218055.
- R. Cole, M. Sharir, C.-K. Yap. On k-hulls and related problems // SIAM Journal on Computing. — 1987. — Т. 16, вып. 1. — С. 61–77. — doi:10.1137/0216005.
- D. W. Crowe, T. A. McKee. Sylvester's problem on collinear points // Mathematics Magazine. — Mathematical Association of America, 1968. — Т. 41, вып. 1. — С. 30–34. — doi:10.2307/2687957. — .
- T. L. Dey. Improved bounds for planar k-sets and related problems // Discrete and Computational Geometry. — 1998. — Т. 19, вып. 3. — С. 373–382. — doi:10.1007/PL00009354.
- G. Dirac. Collinearity properties of sets of points. — Quart. J. Math.. — 1951. — Т. 2. — С. 221–227. — doi:10.1093/qmath/2.1.221.
- H. Edelsbrunner. Algorithms in Combinatorial Geometry. — Springer-Verlag, 1987. — (EATCS Monographs in Theoretical Computer Science). — ISBN 978-3-540-13722-1.
- H. Edelsbrunner, L. J. Guibas. Topologically sweeping an arrangement // Journal of Computer and System Sciences. — 1989. — Т. 38, вып. 1. — С. 165–194. — doi:10.1016/0022-0000(89)90038-X.
- H. Edelsbrunner, L. J. Guibas, M. Sharir. The complexity and construction of many faces in arrangements of lines and of segments // Discrete and Computational Geometry. — 1990. — Т. 5, вып. 1. — С. 161–196. — doi:10.1007/BF02187784.
- H. Edelsbrunner, J. O'Rourke, R. Seidel. Constructing arrangements of lines and hyperplanes with applications // SIAM Journal on Computing. — 1986. — Т. 15, вып. 2. — С. 341–363. — doi:10.1137/0215024.
- H. Edelsbrunner, E. Welzl. Constructing belts in two-dimensional arrangements with applications // SIAM Journal on Computing. — 1986. — Т. 15, вып. 1. — С. 271–284. — doi:10.1137/0215019.
- D. Eppstein. Cubic partial cubes from simplicial arrangements // Electronic J. Combinatorics. — 2006. — Т. 13, вып. 1, R79. — С. 1–14. — arXiv:math.CO/0510263.
- D. Eppstein, J.-Cl. Falmagne, S. Ovchinnikov. Media Theory. — Springer-Verlag, 2007.
- D. Eppstein, D. Hart. Proc. 10th ACM/SIAM Symp. Discrete Algorithms (SODA '99). — 1999. — С. 310–316.
- P. Erdős, L. Lovász, A. Simmons, E. G. Straus. A Survey of Combinatorial Theory (Proc. Internat. Sympos., Colorado State Univ., Fort Collins, Colo., 1971). — Amsterdam: North-Holland, 1973. — С. 139–149.
- J. Erickson. Shortest paths in line arrangements. — 1997.
- S. Fortune, V. Milenkovic. Proc. 7th ACM Symp. Computational Geometry (SoCG '91). — 1991. — С. 334–341. — doi:10.1145/109648.109685.
- H. de Fraysseix, P. Ossona de Mendez. Proc. 11th Int. Symp. Graph Drawing (GD 2003). — Springer-Verlag, 2003. — С. 71–85. — (Lecture Notes in Computer Science).
- Z. Füredi, I. Palásti. Arrangements of lines with a large number of triangles. — Proceedings of the American Mathematical Society. — 1984. — Т. 92. — С. 561–566. — doi:10.2307/2045427.
- D. Greene, F. F. Yao. Proc. 27th IEEE Symp. Foundations of Computer Science. — 1986. — С. 143–152. — doi:10.1109/SFCS.1986.19.
- B. Grünbaum. Arrangements and Spreads. — Providence, R.I.: American Mathematical Society, 1972. — Т. 10. — (Regional Conference Series in Mathematics).
- B. Grünbaum. A catalogue of simplicial arrangements in the real projective plane. — 2005.
- L. M. Kelly, W. O. J. Moser. On the number of ordinary lines determined by n points // Canad. J. Math.. — 1958. — Т. 10. — С. 210–219. — doi:10.4153/CJM-1958-024-6.
- F. T. Leighton. Complexity Issues in VLSI. — Cambridge, MA: MIT Press, 1983. — (Foundations of Computing Series).
- F. Levi. Die Teilung der projektiven Ebene durch Gerade oder Pseudogerade // Ber. Math.-Phys. Kl. Sächs. Akad. Wiss. Leipzig. — 1926. — Т. 78. — С. 256–267.
- L. Lovász. On the number of halving lines // Annales Universitatis Scientiarum Budapestinensis de Rolando Eőtvős Nominatae Sectio Mathematica. — 1971. — Т. 14. — С. 107–108.
- J. Matoušek. Lower bounds on the length of monotone paths in arrangements // Discrete and Computational Geometry. — 1991. — Т. 6, вып. 1. — С. 129–134. — doi:10.1007/BF02574679.
- E. Melchior. Über Vielseite der projektiven Ebene // Deutsche Mathematik. — 1940. — Т. 5. — С. 461–475.
- V. Milenkovic. Proc. 30th IEEE Symp. Foundations of Computer Science (FOCS '89). — 1989. — С. 500–505. — doi:10.1109/SFCS.1989.63525.
- Th. Motzkin. The Lines and Planes Connecting the Points of a Finite Set. — Transactions of the American Mathematical Society. — American Mathematical Society, 1951. — Т. 70. — С. 451–464. — doi:10.2307/1990609.
- G. B. Purdy. Triangles in arrangements of lines // Discrete Math.. — 1979. — Т. 25, вып. 2. — С. 157–163. — doi:10.1016/0012-365X(79)90018-9.
- G. B. Purdy. Triangles in arrangements of lines, II // Proceedings of the American Mathematical Society. — 1980. — Т. 79. — С. 77–81. — doi:10.1090/S0002-9939-1980-0560588-4.
- J.-P. Roudneff. Arrangements of lines with a minimum number of triangles are simple // Discrete and Computational Geometry. — 1988. — Т. 3, вып. 1. — С. 97–102. — doi:10.1007/BF02187900.
- Marcus Schaefer. Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers. — Springer-Verlag, 2010. — Т. 5849. — С. 334–344. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-11805-0_32.
- P. W. Shor. Applied Geometry and Discrete Mathematics: The Victor Klee Festschrift / P. Gritzmann, B. Sturmfels. — Providence, R.I.: American Mathematical Society, 1991. — Т. 4. — С. 531–554. — (DIMACS Series in Discrete Mathematics and Theoretical Computer Science).
- J. Steiner. Einige Gesetze über die Theilung der Ebene und des Raumes // J. Reine Angew. Math.. — 1826. — Т. 1. — С. 349–364.
- T. O. Strommer. Triangles in arrangements of lines // Journal of Combinatorial Theory, Series A. — 1977. — Т. 23, вып. 3. — С. 314–320. — doi:10.1016/0097-3165(77)90022-X.
- L. A. Székely. Crossing numbers and hard Erdős problems in discrete geometry // Combinatorics, Probability and Computing. — 1997. — Т. 6, вып. 3. — С. 353–358. — doi:10.1017/S0963548397002976.
- G. Tóth. Point sets with many k-sets // Discrete and Computational Geometry. — 2001. — Т. 26, вып. 2. — С. 187–194. — doi:10.1007/s004540010022.