Оценочная функция Тейла – Сена
В непараметрической статистике существует метод для робастного линейного сглаживания множества точек (простая линейная регрессия), в котором выбирается медиана наклонов всех прямых, проходящих через пары точек выборки на плоскости. Метод называется оценочной функцией Тейла — Сена, оценочной функцией Сена коэффициента наклона[1][2], выбором наклона[3][4], методом одной медианы[5], методом Кендалла робастного приближения прямой [6][7] и робастной прямой Кендалла — Тейла[8]. Метод назван именами Анри Тейла и Пранаба К. Сена, опубликовавшими статьи об этом методе в 1950 и 1968 соответственно, а также именем Мориса Кендалла.
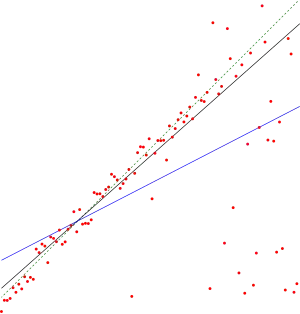
Эта оценочная функция может быть эффективно вычислена и она нечувствительна к выбросам. Она может быть существенно более точна, чем неробастный метод наименьших квадратов для несимметричных и гетероскедастичных данных и хорошо конкурирует с неробастным методом наименьших квадратов даже для нормально распределенных данных в терминах статистической мощности[9]. Метод признан «наиболее популярной непараметрической техникой оценки линейного тренда»[2].
Определение
Как определил Тейл[10], оценочная функция Тейла — Сена множества точек на плоскости (xi,yi) — это медиана m коэффициентов наклона (yj − yi)/(xj − xi) по всем парам точек выборки. Сен[11] расширил это определение для обработки случая, когда две точки имеют одинаковые координаты x. По определению Сена медиана коэффициентов наклона берётся только по парам точек, имеющих различные координаты x.
Когда наклон m вычислен, можно определить прямую из точек выборки путём выбора точки b пересечения оси y, равной медиане значений yi − mxi [12]. Как заметил Сен, это оценочная функция, которая делает τ-коэффициент ранговой корреляции Кендалла сравнения xi с остатком i-го наблюдения приблизительно равным нулю[13].
Доверительный интервал для оценки угла наклона может быть определён как интервал, содержащий средние 95 % значений коэффициентов наклона прямых, проходящих через пары точек[14], и может быть быстро оценён семплированием пар и определением 95%-го интервала семплированных коэффициентов наклона. Согласно численному моделированию, выборка примерно 600 пар точек достаточна для определения точного доверительного интервала[9].
Вариации
Вариантом оценочной функции Тейла — Сена по Сигелу[15] определяет для каждой точки выборки (xi,yi) медиану mi коэффициентов наклона (yj − yi)/(xj − xi) прямых, проходящих через эту точку, а затем вычисляется общая оценочная функция как медиана этих медиан.
Другой вариант выбирает пары точек выборки по рангу их x-координат (точке с наименьшей координатой выбирается в пару первая точка выше координаты медианы и т. д.), затем вычисляются коэффициенты наклона прямых, определяемых этими парами точек[16].
Изучаются также варианты оценочной функции Тейла — Сена, базирующиеся на взвешенных медианах, основанные на принципе, что пары выборок, x-координаты которых отличаются больше, более вероятно имеют более точный наклон, а потому должны иметь больший вес[17]
Для сезонных данных может быть уместным сглаживать сезонные переменные в данных путём отбора пар точек выборки, которые принадлежат одному месяцу или тому же сезону года, а уж затем вычислять медиану коэффициентов наклона прямых, определённых этими ограниченными парами[18].
Статистические свойства
Оценочная функция Тейла — Сена является несмещённой оценкой истинного наклона в простой линейной регрессии[19][20]. Для многих распределений неслучайной ошибки эта оценочная функция имеет высокую асимптотическую эффективность относительно метода наименьших квадратов[21][22]. Оценочные функции с низкой эффективностью требуют больше независимых наблюдений, чтобы достичь той же дисперсии, что и при эффективных несмещённых оценочных функциях.
Оценочная функция Тейла — Сена более робастна, чем оценочная функция метода наименьших квадратов, поскольку она существенно более устойчива к выбросам. Она имеет порог , что означает, что она может допустить искажение до 29,3 % входных данных без уменьшения точности[12]. Однако порог уменьшается для многомерных обобщений метода[23]. Более высокий порог, 50 %, имеется у другого робастного алгоритма линейной оценки, повторной медианной оценочной функции Сигела[12].
Оценочная функция Тейла — Сена является эквивариантной при любом линейном преобразовании её переменных отклика, что означает, что преобразование данных с последующим построением оценивающей прямой и построение прямой с последующим преобразованием данных приводит к одинаковым результатам[24]. Однако оценочная функция не является эквивариантной при одновременном аффинном преобразовании как предикторных переменных, так и переменных отклика[23].
Алгоритмы
Медиана коэффициента наклона множества n точек выборки может быть вычислена точно путём вычисления всех O(n2) прямых через пары точек и применения алгоритма линейного времени для выбора медианы. Альтернативно, значение может быть оценено путём выборки пар точек. Задача эквивалентна, согласно проективной двойственности, задаче нахождения точки пересечения конфигурации прямых, которой принадлежит медиана x координат среди всех таких точек пересечения.[25]
Задача выбора коэффициента наклона точно, но эффективнее, чем грубый квадратичный перебор, интенсивно изучалась в вычислительной геометрии. Известны некоторые другие методы точного вычисления оценочной функции Тейла — Сена за время O(n log n) либо детерминированно[3], либо с использованием вероятностных алгоритмов[4]. Повторная медианная оценка Сигела может быть также построена эффективно за то же время[26]. В моделях вычислений, в которых входные координаты являются целыми числами и битовые операции над целыми числами берут постоянное время, задача может быть решена даже быстрее, с математическим ожиданием времени вычисления [27].
Оценочная функция коэффициента наклона с примерным рангом медианы, имеющая тот же порог, что и оценочная функция Тейла — Сена, может быть получена в поточной модели данных (в которой точки выборки обрабатываются алгоритмом одна за другой, и алгоритм не имеет достаточной памяти для постоянного хранения всего множества данных), используя алгоритм, основанный на ε-сетях[28].
Приложения
Оценочная функция Тейла — Сена была использована в астрономии ввиду возможности работать с цензурированными моделями регрессии[29]. Фернандес и Леблан предложили использовать её в биофизике[30] дистанционного зондирования, такого как оценка листовой поверхности путём измерения отражения, ввиду «простоты вычисления, аналитической оценки доверительного интервала, робастности по отношению к выбросам, проверяемые допущения относительно погрешности и … ограниченной априори информации относительно ошибок измерения». Для измерения сезонных данных окружающей среды, таких как качество воды, был предложен сезонный вариант оценочной функции Тейла — Сена как более предпочтительный по сравнению с методом наименьших квадратов, поскольку он даёт более высокую точность в случае асимметричных данных[18]. В информатике метод Тейла — Сена использовался для оценки тренда устаревания программного обеспечения[31]. Другое применение теста Тейла — Сена наблюдается в метеорологии и климатологии[32], где используется для оценки устойчивых тенденций направления и скорости ветров.
См. также
- Регрессионное разведение, другая проблема, использующая оценивание тренда наклона
Примечания
- Gilbert, 1987.
- El-Shaarawi, Piegorsch, 2001.
- Cole, Salowe, Steiger, Szemerédi, 1989; Katz, Sharir, 1993; Brönnimann, Chazelle, 1998.
- Dillencourt, Mount, Netanyahu, 1992; Matoušek, 1991; Blunck, Vahrenhold, 2006.
- Massart, Vandeginste, и др., 1997.
- Sokal, Rohlf, 1995.
- Dytham, 2011.
- Granato, 2006.
- Wilcox, 2001.
- Theil, 1950.
- Sen, 1968.
- Rousseeuw, Leroy, 2003, с. 67, 164.
- Osborne, 2008.
- Для определения доверительных интервалов пары точек должны быть семплированы с возвратом. Это означает, что множество пар, используемых в этом вычислении, включает полностью совпадающие пары. Эти пары всегда выбрасываются из доверительного интервала, поскольку они не определяют какого-либо конкретного коэффициента наклона, но учёт их при вычислениях делает доверительный интервал шире.
- Siegel, 1982.
- De Muth, 2006.
- Jaeckel, 1972; Scholz, 1978; Sievers, 1978; Birkes, Dodge, 1993.
- Hirsch, Slack, Smith, 1982.
- Sen, 1968, с. 1384 Theorem 5.1.
- Wang, Yu, 2005.
- Sen, 1968, с. Section 6.
- Wilcox, 1998.
- Wilcox, 2005.
- Sen, 1968, с. 1383.
- Cole, Salowe, Steiger, Szemerédi, 1989.
- Matoušek, Mount, Netanyahu, 1998.
- Chan, Pătraşcu, 2010.
- Bagchi, Chaudhary, Eppstein, Goodrich, 2007.
- Akritas, Murphy, LaValley, 1995.
- Fernandes, Leblanc, 2005.
- Vaidyanathan, Trivedi, 2005.
- Romanić, Ćurić, Jovičić, Lompar, 2015, с. 288-302.
Литература
- D. Romanić, M. Ćurić, I. Jovičić, M. Lompar. Long-term trends of the ‘Koshava’ wind during the period 1949–2010. // International Journal of Climatology. — 2015. — Т. 35, вып. 2. — С. 288-302. — doi:10.1002/joc.3981.
- Michael G. Akritas, Susan A. Murphy, Michael P. LaValley. The Theil-Sen estimator with doubly censored data and applications to astronomy // Journal of the American Statistical Association. — 1995. — Т. 90, вып. 429. — С. 170–177. — doi:10.1080/01621459.1995.10476499. — .
- Amitabha Bagchi, Amitabh Chaudhary, David Eppstein, Michael T. Goodrich. Deterministic sampling and range counting in geometric data streams // ACM Transactions on Algorithms. — 2007. — Т. 3, вып. 2. — С. Art. No. 16. — doi:10.1145/1240233.1240239. — arXiv:cs/0307027.
- David Birkes, Yadolah Dodge. Alternative Methods of Regression. — Wiley-Interscience, 1993. — Т. 282. — С. 113–118. — (Wiley Series in Probability and Statistics). — ISBN 978-0-471-56881-0.
- Henrik Blunck, Jan Vahrenhold. International Symposium on Algorithms and Complexity. — Berlin: Springer-Verlag, 2006. — Т. 3998. — С. 30–41. — (Lecture Notes in Computer Science). — ISBN 978-3-540-34375-2. — doi:10.1007/11758471_6.
- Hervé Brönnimann, Bernard Chazelle. Optimal slope selection via cuttings // Computational Geometry Theory and Applications. — 1998. — Т. 10, вып. 1. — С. 23–29. — doi:10.1016/S0925-7721(97)00025-4.
- Timothy M. Chan, Mihai Pătraşcu. Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '10). — 2010. — С. 161–173.
- Richard Cole, Jeffrey S. Salowe, W. L. Steiger, Endre Szemerédi. An optimal-time algorithm for slope selection // SIAM Journal on Computing. — 1989. — Т. 18, вып. 4. — С. 792–810. — doi:10.1137/0218055.
- E. James De Muth. Basic Statistics and Pharmaceutical Statistical Applications. — 2nd. — CRC Press, 2006. — Т. 16. — (Biostatistics). — ISBN 978-0-8493-3799-4.
- Michael B. Dillencourt, David Mount, Nathan Netanyahu. A randomized algorithm for slope selection // International Journal of Computational Geometry & Applications. — 1992. — Т. 2, вып. 1. — С. 1–27. — doi:10.1142/S0218195992000020.
- Calvin Dytham. Choosing and Using Statistics: A Biologist's Guide. — 3rd. — John Wiley and Sons, 2011. — ISBN 978-1-4051-9839-4.
- Abdel H. El-Shaarawi, Walter W. Piegorsch. Encyclopedia of Environmetrics, Volume 1. — John Wiley and Sons, 2001. — ISBN 978-0-471-89997-6.
- Richard Fernandes, Sylvain G. Leblanc. Parametric (modified least squares) and non-parametric (Theil–Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors // Remote Sensing of Environment. — 2005. — Т. 95, вып. 3. — С. 303–316. — doi:10.1016/j.rse.2005.01.005.
- Richard O. Gilbert. Statistical Methods for Environmental Pollution Monitoring. — John Wiley and Sons, 1987. — С. 217–219. — ISBN 978-0-471-28878-7.
- Gregory E. Granato. Kendall-Theil Robust Line (KTRLine--version 1.0)-A visual basic program for calculating and graphing robust nonparametric estimates of linear-regression coefficients between two continuous variables. — U.S. Geological Survey, 2006. — С. 31 with CD–ROM. — (Techniques and Methods of the U.S. Geological Survey, book 4, chap. A7).
- Robert M. Hirsch, James R. Slack, Richard A. Smith. Techniques of trend analysis for monthly water quality data // Water Resources Research. — 1982. — Т. 18, вып. 1. — С. 107–121. — doi:10.1029/WR018i001p00107. — .
- Louis A. Jaeckel. Estimating regression coefficients by minimizing the dispersion of the residuals // Annals of Mathematical Statistics. — 1972. — Т. 43, вып. 5. — С. 1449–1458. — doi:10.1214/aoms/1177692377.
- Matthew J. Katz, Micha Sharir. Optimal slope selection via expanders // Information Processing Letters. — 1993. — Т. 47, вып. 3. — С. 115–122. — doi:10.1016/0020-0190(93)90234-Z.
- D. L. Massart, B. G. M. Vandeginste, L. M. C. Buydens, S. De Jong, P. J. Lewi, J. Smeyers-Verbeke. Handbook of Chemometrics and Qualimetrics: Part A. — Elsevier, 1997. — Т. 20A. — С. 355–356. — (Data Handling in Science and Technology). — ISBN 978-0-444-89724-4.
- Jiří Matoušek. Randomized optimal algorithm for slope selection // Information Processing Letters. — 1991. — Т. 39, вып. 4. — С. 183–187. — doi:10.1016/0020-0190(91)90177-J.
- Jiří Matoušek, David M. Mount, Nathan S. Netanyahu. Efficient randomized algorithms for the repeated median line estimator // Algorithmica. — 1998. — Т. 20, вып. 2. — С. 136–150. — doi:10.1007/PL00009190.
- Jason W. Osborne. Best Practices in Quantitative Methods. — Sage Publications, Inc., 2008. — ISBN 9781412940658.
- Peter Rousseeuw, Annick M. Leroy. Robust Regression and Outlier Detection. — Wiley, 2003. — Т. 516. — (Wiley Series in Probability and Mathematical Statistics). — ISBN 978-0-471-48855-2.
- Friedrich-Wilhelm Scholz. Weighted median regression estimates // The Annals of Statistics. — 1978. — Т. 6, вып. 3. — С. 603–609. — doi:10.1214/aos/1176344204. — .
- Pranab Kumar Sen. Estimates of the regression coefficient based on Kendall's tau. — Journal of the American Statistical Association. — 1968. — Т. 63. — С. 1379–1389. — doi:10.2307/2285891.
- Andrew F. Siegel. Robust regression using repeated medians // Biometrika. — 1982. — Т. 69, вып. 1. — С. 242–244. — doi:10.1093/biomet/69.1.242.
- Gerald L. Sievers. Weighted rank statistics for simple linear regression // Journal of the American Statistical Association. — 1978. — Т. 73, вып. 363. — С. 628–631. — doi:10.1080/01621459.1978.10480067. — .
- Robert R. Sokal, F. James Rohlf. Biometry: The Principles and Practice of Statistics in Biological Research. — Macmillan, 1995. — ISBN 978-0-7167-2411-7.
- H. Theil. A rank-invariant method of linear and polynomial regression analysis. I, II, III // Nederl. Akad. Wetensch., Proc.. — 1950. — Т. 53. — С. 386–392, 521–525, 1397–1412..
- Kalyanaraman Vaidyanathan, Kishor S. Trivedi. A Comprehensive Model for Software Rejuvenation // IEEE Transactions on Dependable and Secure Computing. — 2005. — Т. 2, вып. 2. — С. 124–137. — doi:10.1109/TDSC.2005.15.
- Xueqin Wang, Qiqing Yu. Unbiasedness of the Theil–Sen estimator // Journal of Nonparametric Statistics. — 2005. — Т. 17, вып. 6. — С. 685–695. — doi:10.1080/10485250500039452.
- Rand R. Wilcox. A note on the Theil–Sen regression estimator when the regressor Is random and the error term Is heteroscedastic // Biometrical Journal. — 1998. — Т. 40, вып. 3. — С. 261–268. — doi:10.1002/(SICI)1521-4036(199807)40:3<261::AID-BIMJ261>3.0.CO;2-V.
- Rand R. Wilcox. Fundamentals of Modern Statistical Methods: Substantially Improving Power and Accuracy. — Springer-Verlag, 2001. — С. 207–210. — ISBN 978-0-387-95157-7.
- Rand R. Wilcox. Introduction to Robust Estimation and Hypothesis Testing. — Academic Press, 2005. — С. 423–427. — ISBN 978-0-12-751542-7.
Ссылки
- Kendall-Theil Robust Line (KTRLine—version 1.0) бесплатная программа на Visual Basic для оценки Тейла — Сена, выпущенная Геологической службой США