Прямая
Пряма́я — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий[1], их свойства и связь с другими понятиями (например, точки и плоскости) определяются аксиомами геометрии[2].

Прямая, наряду с окружностью, относится к числу древнейших геометрических фигур. Античные геометры считали эти две кривые «совершенными» и поэтому признавали только построения с помощью циркуля и линейки. Евклид описал линию как «длину без ширины», которая «равно лежит на всех своих точках»[3].
Аналоги прямых могут быть определены также в некоторых типах неевклидовых пространств. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то отрезок прямой можно определить как самую короткую кривую, соединяющую эти точки. Например, в римановой геометрии роль прямых играют геодезические линии, которые являются кратчайшими; на сфере кратчайшими являются дуги больших кругов[4].
Свойства прямой в евклидовой геометрии
Участки прямой, ограниченные двумя её точками, называются отрезками.
- Через любую точку можно провести бесконечно много прямых.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке[5], или являются параллельными (следует из предыдущего).
- В трёхмерном пространстве существуют три варианта взаимного расположения двух несовпадающих прямых:
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
- Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости
или .
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
где и — произвольные постоянные, причём постоянные и не равны нулю одновременно.
При прямая параллельна оси , при — параллельна оси .
Вектор с координатами называется нормальным вектором, он перпендикулярен прямой.
При прямая проходит через начало координат.
Также уравнение можно переписать в виде
Уравнение прямой с угловым коэффициентом
Уравнение прямой линии, пересекающей ось в точке и образующей угол с положительным направлением оси :
Коэффициент называется угловым коэффициентом прямой.
В этом виде невозможно представить прямую, параллельную оси (Иногда в этом случае формально говорят, что угловой коэффициент «обращается в бесконечность».)

Уравнение прямой в отрезках
Уравнение прямой линии, пересекающей ось в точке и ось в точке :
В этом виде невозможно представить прямую, проходящую через начало координат.
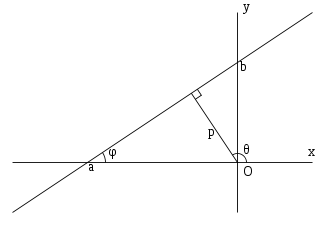
Нормальное уравнение прямой
где — длина перпендикуляра, опущенного на прямую из начала координат, а — угол (измеренный в положительном направлении) между положительным направлением оси и направлением этого перпендикуляра. Если , то прямая проходит через начало координат, а угол задаёт угол наклона прямой.
Пусть дана прямая Тогда и Рассмотрим для этого перпендикуляра его орт Допустим, что угол между и осью равен Так как то можно записать: Теперь рассмотрим произвольную точку Проведём радиус-вектор Теперь найдём проекцию на вектор Следовательно, Это и есть нормальное уравнение прямой. ■
Если прямая задана общим уравнением то отрезки и отсекаемые ею на осях, угловой коэффициент расстояние прямой от начала координат и выражаются через коэффициенты , и следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие В этом случае и являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если то прямая проходит через начало координат и выбор положительного направления произволен.
Уравнение прямой, проходящей через две заданные несовпадающие точки
Если заданы две несовпадающие точки с координатами и , то прямая, проходящая через них, задаётся уравнением
или
или в общем виде

Векторное параметрическое уравнение прямой
Векторное параметрическое уравнение прямой задается вектором конец которого лежит на прямой, и направляющим вектором прямой Параметр пробегает все действительные значения.
Параметрические уравнения прямой
Параметрические уравнения прямой могут быть записаны в виде:
где — произвольный параметр, — координаты и направляющего вектора прямой. При этом
Смысл параметра аналогичен параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где — координаты и направляющего вектора прямой, и координаты точки, принадлежащей прямой.
Тангенциальное уравнение прямой
Тангенциальное уравнение прямой на плоскости:
Числа и называются её тангенциальными, линейными или плюккеровыми координатами.
Уравнения прямой в пространстве
Векторное параметрическое уравнение прямой в пространстве:
где — радиус-вектор некоторой фиксированной точки лежащей на прямой, — ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором), — радиус-вектор произвольной точки прямой.
Параметрические уравнения прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой[уточнить] в пространстве:
- Поскольку прямая является пересечением двух различных плоскостей, заданных соответственно общими уравнениями:
- и
то уравнение прямой можно задать системой этих уравнений:
Векторное уравнение прямой в пространстве[6]:196-199:
- Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :
где фиксированный вектор , ортогональный вектору , можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.
Взаимное расположение точек и прямых на плоскости
Три точки , и лежат на одной прямой тогда и только тогда, когда выполняется условие
Отклонение точки от прямой может быть найдено по формуле
где знак перед радикалом противоположен знаку Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
В пространстве расстояние от точки до прямой, заданной параметрическим уравнением
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент этой точки может быть найден по формуле
Взаимное расположение нескольких прямых на плоскости
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол между пересекающимися прямыми определяется формулой
При этом под понимается угол, на который надо повернуть первую прямую (заданную параметрами , , , и ) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если или , и перпендикулярны, если или .
Любую прямую, параллельную прямой с уравнением можно выразить уравнением При этом расстояние между этими прямыми будет равно
Если же уравнение прямой задано как , а уравнение прямой параллельной ей , то расстояние можно вычислить, как
Если знак перед радикалом противоположен то будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если и , то прямые и перпендикулярны.
Некоторые специальные типы прямых
- Прямая Александрова
- Прямая Симсона
- Прямая Суслина
- Прямая Эйлера
- Числовая прямая
Примечания
- Coxeter, 1969, p. 4
- Математическая энциклопедия, 1984, с. 721—722.
- Прокл Диадох. Комментарий к первой книге «Начал» Евклида / Университет Дмитрия Пожарского. — М., 2013. — С. 116. — 368 с.
- Норден А. П. Краткий курс дифференциальной геометрии. — М.: Физматгиз, 1958. — С. 214—215. — 244 с.
- Faber, Appendix B, p. 300.
- Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
Литература
- Маркушевич А. И. Замечательные кривые, Популярные лекции по математике. — Выпуск 4. — Гостехиздат, 1952 г. — 32 стр.
- Прямая // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
- Coxeter, H.S.M (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 0-471-18283-4
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, ISBN 0-8247-1748-1
- Pedoe, Dan (1988), Geometry: A Comprehensive Course, Mineola, NY: Dover, ISBN 0-486-65812-0
- Wylie, Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill, ISBN 0-07-072191-2
