Строфоида

Строфоида (от греч. στροφή — поворот) — алгебраическая кривая 3-го порядка. Строится следующим образом (см. Рис. 1):

Рис. 1

Рис. 2

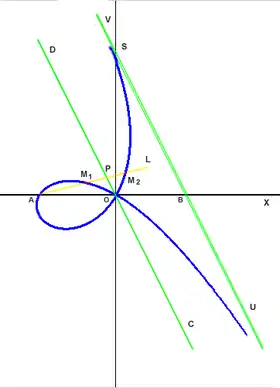
В декартовой системе координат, где ось абсцисс направлена по OX, а ось ординат по OD, задана фиксированная точка A на оси OX. Через т. А проводится произвольная прямая AL, которая пересекает ось ординат в точке P. От точки P, на расстоянии равном OP, в обе стороны вдоль прямой AL находятся точки M1 и M2. Геометрическое место точек M1 и M2 образуют строфоиду.

В прямоугольной системе координат строится прямая строфоида или просто строфоида, которая изображена на Рис.1. В косоугольной системе координат строится косая строфоида — Рис.2.

Уравнения

Уравнение строфоиды в декартовой системе координат, где O — начало координат, ось абсцисс направлена по лучу OB, ось ординат по лучу OD, угол $\alpha =\angle AOD$ (для прямоугольной системы координат $\alpha ={\frac {\pi }{2}}$ ), записывается так:

y^{2}\left(x-a\right)-2x^{2}y\cos \alpha +x^{2}\left(a+x\right)=0

.

Уравнение прямой строфоиды:

y=\pm x{\sqrt {\frac {a+x}{a-x}}}

.

Уравнение строфоиды в полярной системе координат:

\rho =-{\frac {a\cos 2\phi }{\cos \phi }}

.

Параметрическое уравнение строфоиды:

x=a\left({\frac {u^{2}-1}{u^{2}+1}}\right)

y=au\left({\frac {u^{2}-1}{u^{2}+1}}\right)

, где

u=\mathrm {tg} \,\phi

.

Точка B отстоит от центра координат O на расстоянии равном a=OA. Прямая UV, проведенная через точку B параллельно оси ординат служит асимптотой для обеих ветвей прямой строфоиды. Для косой строфоиды, прямая UV служит асимптотой для нижней ветви и касательной в точке S, причём SB = SA.

В точке O существуют две касательные, которые взаимно перпендикулярны, как для прямой, так и для косой строфоиды.

История

Считается, что строфоида впервые была рассмотрена французским математиком Жилем Робервалем в 1645 году. Он называл эту кривую «птероидой» (от греч. πτερον— крыло). Название «строфоида» было введено в 1849 году.

Дальнейшее относится только к прямой строфоиде.

Нахождение касательной

y'={\sqrt {\frac {a+x}{a-x}}}\left(1+{\frac {ax}{a^{2}-x^{2}}}\right)

В точке $O(0,0)$ производная $y'=\pm 1$ , то есть в точке $O(0,0)$ существуют две перпендикулярные касательные, угол наклона которых равен $\pm {\frac {\pi }{4}}$ .

Вывод

Тангенс угла наклона касательной равен значению первой производной функции. Перепишем уравнение строфоиды (прямой) в следующем виде:

y=xz

, где

z={\sqrt {\frac {a+x}{a-x}}}

.

y'=z+xz'

z={\sqrt {\frac {a+x}{a-x}}}

\ln {z}={\frac {1}{2}}\ln {a+x}-{\frac {1}{2}}\ln {a-x}

Дифференцируем данное уравнение:

{\frac {z'}{z}}={\frac {1}{2}}{\frac {1}{a+x}}+{\frac {1}{2}}{\frac {1}{a-x}}={\frac {a}{a^{2}-x^{2}}}

{\frac {z'}{z}}={\frac {1}{2}}{\frac {1}{a+x}}+{\frac {1}{2}}{\frac {1}{a-x}}={\frac {a}{a^{2}-x^{2}}}

z'={\frac {a}{a^{2}-x^{2}}}{\sqrt {\frac {a+x}{a-x}}}

отсюда

y'={\sqrt {\frac {a+x}{a-x}}}\left(1+{\frac {ax}{a^{2}-x^{2}}}\right)

Радиус кривизны

$R=ON$ в точке $O(0,0)$ определяется так:

R={\frac {a}{\cos \angle AON}}={\frac {a}{\cos {\frac {\pi }{4}}}}=a{\sqrt {2}}

.

Площадь петли строфоиды и площадь между строфоидой и асимптотой

Площадь петли строфоиды слева от оси ординат

S_{1}=a^{2}(2-{\frac {\pi }{2}})

.

Площадь между строфоидой и асимптотой справа от оси ординат

S_{1}=a^{2}(2+{\frac {\pi }{2}})

.

Вывод

Уравнение верхней дуги $AM_{1}O$ :

y=-x{\sqrt {\frac {a+x}{a-x}}}\qquad

(1)

Половина площади левой петли строфоиды равна интегралу от уравнения (1) в пределах от $-a$ до $0$ .

{\frac {1}{2}}S_{1}=-\int \limits _{-a}^{0}x{\sqrt {\frac {a+x}{a-x}}}\,dx\qquad

(2)

Подстановка:

u=a-x,\qquad a+x=2a-u,\qquad dx=-du

.

Пределы интегрирования:

x=-a\Rightarrow \;u=2a,\qquad x=0\Rightarrow \;u=a

Интеграл (2) преобразуется к виду:

{\frac {1}{2}}S_{1}=\int \limits _{2a}^{a}\left(a-u\right){\sqrt {\frac {2a-u}{u}}}\,du=

=-\int \limits _{2a}^{a}u{\sqrt {\frac {2a-u}{u}}}\,du+a\int \limits _{2a}^{a}{\sqrt {\frac {2a-u}{u}}}\,du\qquad

(3)

Первый интеграл из уравнения (3):

-\int \limits _{2a}^{a}u{\sqrt {\frac {2a-u}{u}}}\,du=-\int \limits _{2a}^{a}{\sqrt {2au-u^{2}}}\,du\qquad

(4)

Подстановка:

v=u-a,\qquad u=v+a,\qquad dv=du

.

Пределы интегрирования:

u=2a\Rightarrow \;v=a,\qquad u=a\Rightarrow \;v=0

.

Интеграл (4) преобразуется к виду:

-\int \limits _{a}^{0}{\sqrt {2a\left(v+a\right)-\left(v+a\right)^{2}}}\,dv=-\int \limits _{a}^{0}{\sqrt {a^{2}-v^{2}}}\,dv=

=-\left[{\frac {v}{2}}{\sqrt {a^{2}-v^{2}}}+{\frac {a^{2}}{2}}\arcsin {\frac {v}{a}}\right]{\begin{cases}0\\a\end{cases}}=

={\frac {a^{2}}{2}}\arcsin 1={\frac {a^{2}\pi }{4}}

.

Второй интеграл из уравнения (3):

a\int \limits _{2a}^{a}{\sqrt {\frac {2a-u}{u}}}\,du\qquad

(5)

Подстановка:

u=v^{2},\qquad du=2vdv

.

Пределы интегрирования:

u=2a\Rightarrow \;v={\sqrt {2a}},\qquad u=a\Rightarrow \;v={\sqrt {a}}

.

Интеграл (5) преобразуется к виду:

2a\int \limits _{\sqrt {2a}}^{\sqrt {a}}{\sqrt {2a-v^{2}}}\,dv=

=2a\left[{\frac {v}{2}}{\sqrt {2a-v^{2}}}+a\arcsin {\frac {v}{\sqrt {2a}}}\right]{\begin{cases}{\sqrt {a}}\\{\sqrt {2a}}\end{cases}}=

=-{\frac {a^{2}\pi }{2}}+a^{2}

.

Итак:

{\frac {1}{2}}S_{1}={\frac {a^{2}\pi }{4}}-{\frac {a^{2}\pi }{2}}+a^{2}

Площадь $S_{1}$ равна:

S_{1}=2a^{2}-{\frac {a^{2}\pi }{2}}

.

Если координата $x$ стремится к $a$ , то правые ветви строфоиды стремятся к $\pm \infty$ , но площадь между линией $U'OV'$ и асимптотой $UV$ конечна и определяется интегралом (2) в пределах от $0$ до $a$ . В этом случае площадь получится отрицательной, так как уравнение (1) описывает ветвь OU', а площадь, заключенная между этой ветвью и лучом OX и лучом BU — отрицательна. Если вычислить интеграл (2) в пределах от $0$ до $a$ , получим следующее выражение для площади $S_{2}$ :

S_{2}=2a^{2}+{\frac {a^{2}\pi }{2}}

.

Объём тела вращения

Объём ( $V_{1}$ ) тела, образованного при вращении дуги $OM_{1}A$ вокруг оси абсцисс, рассчитывается так:

V_{1}=\pi \int \limits _{-a}^{0}\left(x{\sqrt {\frac {a+x}{a-x}}}\right)^{2}\,dx=\qquad

(6)

=\pi \int \limits _{-a}^{0}x^{2}{\frac {a+x}{a-x}}\,dx=

=-\pi \int \limits _{-a}^{0}x^{2}\,dx-2\pi a\int \limits _{-a}^{0}x\,dx-2\pi a^{2}\int \limits _{-a}^{0}dx+2\pi a^{3}\int \limits _{-a}^{0}{\frac {dx}{a-x}}=

=-{\frac {a^{3}\pi }{3}}+a^{3}\pi -2a^{3}\pi +2a^{3}\pi \ln {2}

Итак:

V_{1}=a^{3}\pi \left(2\ln {2}-{\frac {4}{3}}\right)

.

Объём ( $V_{2}$ ) тела, образованного при вращении ветви $OV'$ вокруг оси абсцисс, стремится к бесконечности. Этот объём вычисляется из интеграла (6) в пределах от $0$ до $b$ , где $0=<b<a$ :

V_{2}=\pi \int \limits _{0}^{b}\left(x{\sqrt {\frac {a+x}{a-x}}}\right)^{2}\,dx=\qquad

=-\pi \int \limits _{0}^{b}x^{2}\,dx-2\pi a\int \limits _{0}^{b}x\,dx-2\pi a^{2}\int \limits _{0}^{b}dx+2\pi a^{3}\int \limits _{0}^{b}{\frac {dx}{a-x}}=

=-{\frac {\pi b^{3}}{3}}-a\pi b^{2}-2a^{2}\pi b+2a^{3}\pi \left(\ln {a}-\ln {\left(a-b\right)}\right)

.

Если $b\Rightarrow \;a$ , то $\ln {\left(a-b\right)}\Rightarrow \;-\infty$ , то есть $V_{2}\Rightarrow \;\infty$ .

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.