Улитка Паскаля
Улитка Паскаля ― плоская кривая определённого типа. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
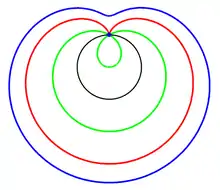
Три улитки Паскаля, конхоиды чёрной окружности: зелёная , красная (кардиоида) и синяя
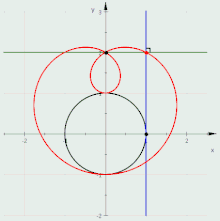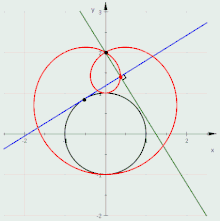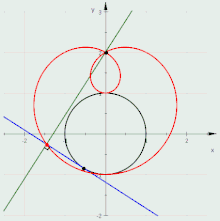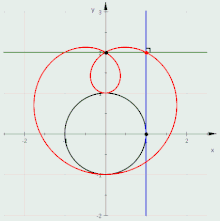
Анимация подеры окружности
Уравнения
Уравнение в прямоугольных координатах:
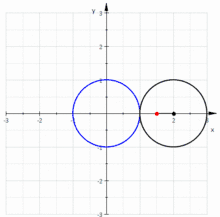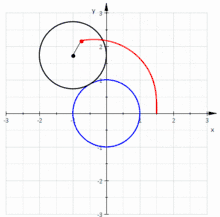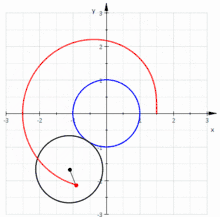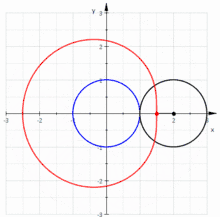
Построение улитки Паскаля
параметрическое:
Здесь a — диаметр исходной окружности, а — расстояние, на которое смещается точка вдоль радиус-вектора (см. конхоида).
При этом начало координат является
- узловой точкой при ,
- точкой возврата при (в этом случае улитка Паскаля называется кардиоидой),
- двойной точкой при .
В случае улитка Паскаля также называется трисектри́са. Такое название она получила из-за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки. Уравнение трисектрисы:
в полярных координатах:
Свойства
- Улитка Паскаля является плоской алгебраической кривой 4-го порядка.
- Улитка Паскаля является обобщением кардиоиды.
- Улитка Паскаля является подерой окружности.
- Улитка Паскаля является конхоидой окружности относительно точки на окружности.
- Улитка Паскаля является частным случаем Декартова овала.
- Улитка Паскаля является частным случаем эпитрохоиды.
- Улитка Паскаля является примером эквихордной кривой.
- Длина дуги выражается эллиптическим интегралом 2-го рода.
- Площадь, ограниченная улиткой Паскаля:
- При площадь внутренней петли при вычислении по этой формуле считается дважды.
Литература
- Улитка Паскаля // Ужи — Фидель. — М. : Советская энциклопедия, 1956. — С. 188—189. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 44).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.