Конфигурация (разбиение пространства)

Конфигурация — это разбиение d-мерного линейного, аффинного или проективного пространства на связные открытые ячейки, порождённые конечным набором геометрических объектов. Иногда эти объекты имеют один и тот же тип, такой как гиперплоскости или сферы. Интерес к изучению конфигураций вызван успехами в вычислительной геометрии, где конфигурации были объединяющими структурами для многих задач. Успехи в изучении более сложных объектов, таких как алгебраические поверхности, отвечали нуждам приложений «реального мира», таких как планирование движений и компьютерное зрение[1].

Конфигурация прямых

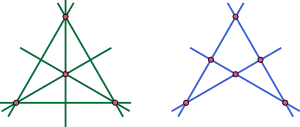
Особый интерес представляют конфигурации прямых и конфигурации гиперплоскостей.

В общем случае геометры изучают конфигурации других типов кривых на плоскости и других более сложных типов поверхностей[2].

Изучаются и конфигурации в комплексных векторных пространствах. Поскольку комплексная прямая не разбивает комплексную плоскость на несколько компонент, комбинаторика вершин, рёбер и ячеек не подходит для этого типа пространств, но представляет интерес изучение симметрий и топологических свойств[3].

Примечания
  1. Halperin, 2004.
  2. Agarwal, Sharir, 2000, с. 49–119.
  3. Orlik, Terao, 1992.

Литература
  • Dan Halperin. Arrangements // Handbook of Discrete and Computational Geometry. — 2nd. — 2004. — ISBN 978-1-58488-301-2.
  • Agarwal P. K., Sharir M. Arrangements and their applications // Handbook of Computational Geometry / Sack J.-R., Urrutia J.. — Elsevier, 2000.
  • Orlik P., Terao H. Arrangements of Hyperplanes. — Springer-Verlag, 1992. — Т. 300. — (Grundlehren der mathematischen Wissenschaften).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.