Конфигурация (геометрия)

Конфигурация на плоскости обозначается как (p_γ ℓ_π), где p — число точек, ℓ — число прямых, γ — число прямых, проходящих через каждую точку, а π — число точек на каждой прямой. Для этих чисел должно выполняться соотношение

${\displaystyle p\gamma =\ell \pi }$,

поскольку это произведение равно числу инциденций точка-прямая (флагов).

Конфигурации с тем же символом не обязаны быть изоморфными в качестве структур инцидентности. Например, существует три различных конфигурации (9₃ 9₃) — конфигурация Паппа и две менее известные конфигурации.

В некоторых конфигурациях p = ℓ а потому, γ = π. Они называются симметричными или сбалансированными[4] конфигурациями и обычно в обозначениях повторение опускается. Например, (9₃ 9₃) сокращается до (9₃).

Конфигурация (10₃), не изоморфная по инцидентности конфигурации Дезарга

Наиболее известны следующие проективные конфигурации:

• (1₁), простейшая возможная конфигурация, состоящая из точки на прямой. Ввиду тривиальности зачастую не рассматривается.
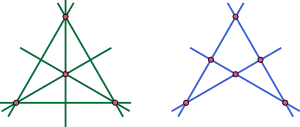
• (3₂), треугольник. Каждая из трёх сторон содержит две из трёх вершин, и наоборот. Обобщённо, любой многоугольник с n сторонами образует конфигурацию типа (n₂)
• (4₃ 6₂) и (6₂ 4₃), полный четырёхугольник и полный четырёхсторонник[1] соответственно.
• (7₃), Плоскость Фано. Эта конфигурация существует как абстрактная геометрия инцидентности, но она не может быть построена на евклидовой плоскости.
• (8₃), конфигурация Мёбиуса — Кантора. Эта конфигурация состоит из двух четырёхугольников, одновременно описанных и вписанных относительно друг друга. Конфигурацию нельзя построить на евклидовой плоскости, но уравнения, её определяющие, имеют нетривиальные решения в комплексных числах.
• (9₃), конфигурация Паппа.
• (9₄ 12₃), Конфигурация Гессе девяти точек перегиба кубики на комплексной проективной плоскости и двенадцати прямых, каждая из которых содержит по три точки. Эта конфигурация имеет то же свойство, что и плоскость Фано, а именно, что она содержит все прямые, проходящие через любые две точки конфигурации. Конфигурации с такими свойствами известны как конфигурации Сильвестра–Галлаи. Для этих конфигураций по теореме Сильвестра они не могут быть реализованы в вещественной плоскости[5].
• (10₃), конфигурация Дезарга.
• (12₅30₂), двойная шестёрка Шлефли, образованная 12 прямыми из 27 прямых на кубической поверхности
• (15₃), конфигурация Кремоны — Ричмонда, образованная 15 прямыми, не входящими в двойную шестёрку, и соответствующими 15 касательными плоскостями
• (12₄ 16₃), конфигурация Рейе.
• (16₆), конфигурация Куммера.
• (27₃), конфигурация Грея
• (60₁₅), конфигурация Клейна.

Проективно двойственной конфигурацией для (p_γ l_π) является конфигурация (l_π p_γ), в которой роли «точек» и «прямых» меняются местами. Поэтому конфигурации идут двойственными парами, за исключением случаев, когда двойственная конфигурация изоморфна исходной. Эти исключения называются самодвойственными конфигурациями и в этих случаях p = l[6].

Число неизоморфных конфигураций типа (n₃), начиная с n = 7, является элементом последовательности

1, 1, 3, 10, 31, 229, 2036, 21399, 245342, ... последовательность A001403 в OEIS

Эти числа подсчитаны как абстрактные структуры инцидентности, независимо от возможности их реализации[7]. Как пишет Гропп[8], девять из десяти конфигураций (10₃) и все конфигурации (11₃) и (12₃) допускают реализацию в евклидовом пространстве, но для всех n ≥ 16 имеется по меньшей мере одна нереализуемая конфигурация (n₃) . Гропп также указывает давнюю ошибку в этой последовательности — в статье 1895 года была попытка перечислить все конфигурации (12₃) и 228 из них были найдены, но 229-я конфигурация не была открыта вплоть до 1988 года.

Имеется несколько методов построения конфигураций, обычно начинающих с уже известных конфигураций. Некоторые простейшие из этих методов строят симметричные (p_γ) конфигурации.

Любая конечная проективная плоскость порядка n является конфигурацией ((n² + n + 1)_{n + 1}). Пусть Π — проективная плоскость порядка n. Удалим из Π точку P и все прямые Π, проходящие через P (но не точки, лежащие на этих прямых, за исключением точки P) и удалим прямую l, не проходящую через P, и все точки, лежащие на этой прямой. В результате получим конфигурацию типа ((n² - 1)_n). Если при построении выберем прямую l, проходящую через P, получим конфигурацию типа ((n²)_n). Поскольку известно, что проективные плоскости существуют для всех порядков n, являющихся степенями простых чисел, эти построения обеспечивают бесконечное семейство симметричных конфигураций.

Не все конфигурации реализуемы, например, конфигурация (43₇) не существует[9]. Однако Групп[10] дал построение, которое показывает, что для k ≥ 3 конфигурация (p_k) существует для всех p ≥ 2 l_k + 1, где l_k является длиной оптимальной линейки Голомба порядка k.

Двойная шестёрка Шлефли

Концепция конфигурации может быть обобщена на более высокие размерности, например для точек и прямых или плоскостей в пространстве. В этом случае ограничение, что никакие две точки не могут лежать более чем на одной прямой, можно ослабить, поскольку две точки могут принадлежать более чем одной плоскости.

В трёхмерном пространстве интересными являются

• Конфигурация Мёбиуса, состоящая из двух взаимно вписанных тетраэдров
• Конфигурация Рейе, состоящая из двенадцати точек и двенадцати плоскостей с шестью точками на каждой плоскости и шестью плоскостями, проходящими через каждую точку
• Конфигурация Грея, состоящая из 27 точек решётки 3×3×3 и 27 ортогональных прямых, проходящих через них
• Двойная шестёрка Шлефли, состоящая из 30 точек и 12 прямых, по две прямые на точку и по пять точек на одной прямой.

Дальнейшее обобщение получается в трёхмерном пространстве при рассмотрении инцидентности точек, прямых и плоскостей, то есть j-пространств при 0 ≤ j < 3, где каждое j-пространство инцидентно N_jk k-пространствам (j ≠ k). Если обозначить через N_jj число j-пространств, такую конфигурацию можно представить в виде матрицы:

${\displaystyle {\begin{vmatrix}{\begin{vmatrix}N_{00}&N_{01}&N_{02}\\N_{10}&N_{11}&N_{12}\\N_{20}&N_{21}&N_{22}\end{vmatrix}}\end{vmatrix}}}$

Подход можно обобщать для других размерностей n, где 0 ≤ j < n. Такие конфигурации математически связаны с правильными многогранниками[11].

• Комплексные многогранники (которые лучше бы называть комплексными конфигурациями)

• Leah W. Berman. Movable (n₄) configurations // The Electronic Journal of Combinatorics. — Т. 13, вып. 1. — С. R104..
• A. Betten, G. Brinkmann, T. Pisanski. Counting symmetric configurations // Discrete Applied Mathematics. — 2000. — Т. 99, вып. 1–3. — С. 331–338. — doi:10.1016/S0166-218X(99)00143-2..
• H.S.M. Coxeter. Regular Polytopes. — Methuen and Co, 1948..
• H.S.M. Coxeter. Self-dual configurations and regular graphs // The Beauty of Geometry. — Dover. — 1999. — ISBN 0-486-40919-8.
• Peter Dembowski. Finite geometries. — Berlin, New York: Springer-Verlag, 1968. — Т. Band 44. — (Ergebnisse der Mathematik und ihrer Grenzgebiete). — ISBN 3-540-61786-8.
• Harald Gropp. On the existence and non-existence of configurations n_k // Journal of Combinatorics and Information System Science. — 1990. — Т. 15. — С. 34–48.
• Harald Gropp. Configurations and their realization // Discrete Mathematics. — 1997. — Т. 174, вып. 1–3. — С. 137–151. — doi:10.1016/S0012-365X(96)00327-5..
• Branko Grünbaum. The Coxeter Legacy: Reflections and Projections / Chandler Davis, Erich W. Ellers. — American Mathematical Society, 2006. — С. 179–225..
• Branko Grünbaum. Configurations of Points and Lines. — American Mathematical Society, 2009. — Т. 103. — (Graduate Studies in Mathematics). — ISBN 978-0-8218-4308-6..
• David Hilbert, Stephan Cohn-Vossen. Geometry and the Imagination. — 2nd. — Chelsea, 1952. — ISBN 0-8284-1087-9..
• L. M. Kelly. A resolution of the Sylvester–Gallai problem of J. P. Serre // Discrete and Computational Geometry. — 1986. — Т. 1, вып. 1. — С. 101–104. — doi:10.1007/BF02187687..
• Tomaž Pisanski, Brigitte Servatius. Configurations from a Graphical Viewpoint. — Springer, 2013. — ISBN 9780817683641..

• Weisstein, Eric W. Configuration (англ.) на сайте Wolfram MathWorld.