Конфигурация Гессе

Конфигурация Гессе — конфигурация 9 точек и 12 прямых с тремя точками на каждой прямой и с четырьмя прямыми, проходящих через каждую точку. Её рассматривал Колин Маклорен и изучал Отто Гессе (1844)[1], Конфигурация реализуема в комплексной проективной плоскости как множество точек перегиба эллиптической кривой, но не существует реализации на евклидовой плоскости.

Конфигурация Гессе с четырьмя прямыми (четыре разбитые диагонали массива 3×3 точек) нарисованными в виде кривых

Описание

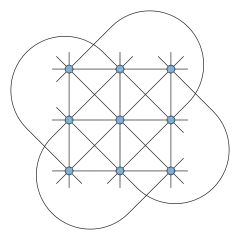
Конфигурация Гессе имеет те же отношения инцидентности, что и прямые и точки аффинной плоскости над полем из 3 элементов. То есть точки конфигурации Гессе можно отождествить с упорядоченными парами целых чисел по модулю 3, а прямые можно соответственно отождествить с тройками точек (x, y), удовлетворяющих линейным уравнениям ax + by = c (mod 3). Альтернативно точки конфигурации можно отождествить с квадратами поля крестики-нолики (3х3), а прямые можно отождествить с прямыми и разбитыми диагоналями[2] поля.

Каждая точка лежит на четырёх прямых — в интерпретации конфигурации как поля крестиков-ноликов, одна прямая горизонтальна, одна вертикальна, и две прямые являются диагоналями или разбитыми диагоналями. Каждая прямая содержит три точки, так что на языке конфигураций конфигурация Гессе имеет запись 94123.

Группа автоморфизмов конфигурации Гессе имеет порядок 216 и известна как гессианова группа.

Связанные конфигурации

Удаление любой точки и инцидентные ей прямые из конфигурации Гессе даёт другую конфигурацию типа 8383, конфигурацию Мёбиуса — Кантора[3][4][5].

В конфигурации Гессе 12 прямых можно сгруппировать в четыре тройки параллельных (непересекающихся) прямых. Удаление из конфигурации Гессе трёх прямых, входящих в одну из троек, даёт конфигурацию типа 9393, конфигурацию Паппа[4][5].

Конфигурация Гессе может быть расширена добавлением четырёх точек, по одной на каждую тройку непересекающихся прямых, и добавлением прямой, содержащей эти новые четыре точки. Такое расширение даёт конфигурацию типа 134134, множество точек и прямых проективной плоскости над трёхэлементным полем.

Реализуемость

Конфигурацию Гессе можно реализовать в комплексной проективной плоскости как 9 точек перегиба эллиптической кривой и 12 прямых, проходящих через тройки точек перегиба. Если заданное множество девяти точек в комплексной плоскости является множеством точек перегиба эллиптической кривой C, оно является множеством точек перегиба любой кривой в пучке кривых, образованном C и её кривой Гессе, пучке Гессе[6].

Конфигурация Гессе вместе с конфигурацией Мёбиуса-Кантора имеют комплексные реализации в комплексном пространстве, но не имеют реализацию с прямыми линиями на евклидовой плоскости. В конфигурации Гессе любые две точки связаны прямой из конфигурации (что является определением конфигурации Сильвестра-Галаи), а потому любая прямая, проходящая через две её точки содержит третью точку. Однако в евклидовом пространстве любое конечное число точек либо коллинеарно, либо, по теореме Сильвестра, включает пару точек, не содержащих точек множества на прямой, проходящей через эти две точки. Так как конфигурация Гессе нарушает теорему Сильвестра, она не может иметь евклидовой реализации. Этот пример показывает, что теорема Сильвестра не может быть обобщена на комплексную проективную плоскость. Однако в комплексных пространствах конфигурация Гессе и все конфигурации Сильвестра-Галаи должны лежать в двумерном плоском подпространстве[7].

Примечания
  1. Hesse, 1844, с. 68–96.
  2. Разбитая диагональ — это набор из n ячеек квадрата, лежащих на двух параллельных диагональных прямых (квадрат n х n)
  3. Dolgachev, 2004, с. 423–462.
  4. Coxeter, 1950, с. 413–455.
  5. Cullinane, Steven H. (2011), Configurations and squares, <http://finitegeometry.org/sc/gen/configs.html>.
  6. Artebani, Dolgachev, 2009, с. 235–273.
  7. Elkies, Pretorius, Swanepoel, 2006, с. 361–373.

Литература
  • Michela Artebani, Igor Dolgachev. The Hesse pencil of plane cubic curves // L'Enseignement Mathématique. Revue Internationale. 2e Série. — 2009. — Т. 55, вып. 3. — С. 235–273. — doi:10.4171/lem/55-3-3. — arXiv:math/0611590.
  • O. Hesse. Über die Elimination der Variabeln aus drei algebraischen Gleichungen vom zweiten Grade mit zwei Variabeln.. — Journal für die Reine und Angewandte Mathematik. — 1844. — Т. 28. — С. 68–96. — doi:10.1515/crll.1844.28.68. (на немецком)
  • Igor V. Dolgachev. The Fano Conference. — Univ. Torino, Turin, 2004. — С. 423–462.
  • H. S. M. Coxeter. Self-dual configurations and regular graphs // Bulletin of the American Mathematical Society. — 1950. — Т. 56, вып. 5. — P. 413–455. — doi:10.1090/S0002-9904-1950-09407-5.
  • Noam Elkies, Lou M. Pretorius, Konrad J. Swanepoel. Sylvester–Gallai theorems for complex numbers and quaternions // Discrete and Computational Geometry. — 2006. — Т. 35, вып. 3. — doi:10.1007/s00454-005-1226-7. — arXiv:math/0403023.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.