Конфигурация Дезарга

Конфигурация Дезарга — конфигурация десяти точек и десяти прямых, в которой каждая прямая содержит три точки конфигурации, и через любую точку проходят три прямых. Конфигурация названа в честь Жерара Дезарга и она тесно связана с теоремой Дезарга, которая доказывает существование таких конфигураций.

Конфигурация Дезарга в виде пары взаимно вписанных пятиугольников: каждая вершина пятиугольника лежит на прямой, проходящей через одну из сторон другого пятиугольника.

Построения

Двухмерное пространство
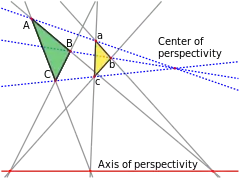
Два треугольника в перспективе, их центр и ось перспективы

Говорят, что два треугольника ABC и abc находятся в центральной перспективе, если прямые Aa, Bb и Cc пересекаются в одной точке (так называемом центре перспективы). Они находятся в осевой перспективе, если точки пересечения прямых, проходящих через соответствующие стороны треугольников X = AB•ab, Y = AC•ac и Z = BC•bc, лежат на одной прямой, на оси перспективы. Теорема Дезарга утверждает, что эти два условия эквивалентны — если два треугольника находятся в центральной перспективе, то они должны находиться и в осевой перспективе, и наоборот. В этом случае десять точек и десять прямых этих двух перспектив (шесть вершин треугольников, три точки пересечения на оси перспективы и центр перспективы, шесть сторон треугольников, три прямых через центр перспективы и ось перспективы) вместе образуют конфигурацию Дезарга.

Трёхмерное пространство

Хотя конфигурацию можно вложить в плоскость, она имеет очень простое построение в трёхмерном пространстве — любые пять плоскостей, находящихся в общем положении в евклидовом пространстве, имеют десять точек пересечения трёх плоскостей и десять прямых пересечения двух плоскостей и образуют конфигурацию Дезарга [1]. Это построение тесно связано со свойством, что любая проективная плоскость, которую можно вложить в проективное пространство, подчиняется теореме Дезарга. Такое трёхмерное представление конфигурации Дезарга называется также полным пятигранником [1].

Четырёхмерное пространство

Пятиячейник или пятигранник (правильный симплекс в четырёхмерном пространстве) имеет пять вершин, десять рёбер, десять треугольных двумерных граней и пять тетраэдальных граней. Рёбра и двумерные грани пересекаются точно таким же образом, как и точки с прямыми в конфигурации Дезарга. Продолжим рёбра пятиячейника прямыми и каждый треугольник до плоскости. Рассмотрим пересечение этих прямых и плоскостей с трёхмерной гиперплоскостью, которая не содержит этих прямых и плоскостей, а также не параллельна им. Каждая прямая пересекает гиперплоскость в точке, а каждая плоскость пересекает гиперплоскость по прямой. Эти десять точек и прямых образуют конфигурацию Дезарга [1].

Симметрии

Хотя в теореме Дезарга точки и прямые играют различные роли, конфигурация Дезарга более симметрична — любая из десяти точек может быть выбрана в качестве центра перспективы, и этот выбор определяет, какие шесть точек будут вершинами треугольников и какая прямая будет осью перспективы. Конфигурация Дезарга имеет группу симметрии порядка 120. Таким образом, имеется 120 различных способов перестановки точек и прямых в конфигурации, сохраняющих инцидентность точки и прямой. Трёхмерное представление конфигурации Дезарга делает эти симметрии более явными — если конфигурация получается из пяти плоскостей в трёхмерном пространстве в общей конфигурации, то каждая из 120 различных перестановок этих пяти плоскостей соответствует симметрии в конфигурации Дезарга [1].

Конфигурация Дезарга самодвойственна, что означает, что можно найти соответствие точек первой конфигурации прямым в другой конфигурации и прямых первой точкам второй таким способом, что все инцидентности сохраняются [2].

Графы

Граф Леви конфигурации Дезарга, имеющий по одной вершине для каждой точки и по одной вершине для каждой прямой в конфигурации, известен как граф Дезарга. Ввиду симметрий и самодвойственности конфигурации Дезарга граф Дезарга является симметричным графом.

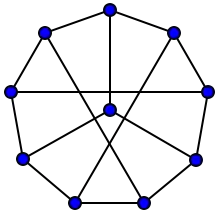
Граф Петерсена в представлении, предложенном Кемпе (Kempe 1886)

Кемпе предложил другой граф для этой конфигурации, имеющий десять вершин, соответствующих прямым, и рёбра, соединяющие две вершины, если точка пересечения двух прямых не принадлежит конфигурации. Можно интерпретировать этот граф другим способом — вершины графа соответствуют точкам конфигурации Дезарга, а рёбра в этом случае соответствуют прямым, если проходящая через эти точки прямая не принадлежит конфигурации. Эта публикация является первым известным источником в математической литературе, в котором появился граф Петерсена, за 12 лет до того, как Юлиус Петерсен использовал тот же граф в качестве контрпримера в задаче рёберной раскраски.

Связанные конфигурации
Конфигурация (103103), не являющаяся дезарговой

Как проективная конфигурация, конфигурация Дезарга имеет обозначение (103103), что означает, что каждая из её 10 точек инцидентна трём прямым, а каждая из 10 прямых инцидентна трём точкам. Её десять точек можно рассматривать единственным способом как два взаимно вписанных пятиугольника или как вписанный в самого себя десятиугольник[3]. Граф Дезарга, двудольный симметричный кубический граф с 20 вершинами, назван этим именем, поскольку его можно представить как граф Леви конфигурации Дезарга, с вершиной для каждой точки и для каждой прямой и ребром для каждой инциденции точка-прямая.

Существует ещё восемь других (103103) конфигураций (то есть множеств точек и прямых в евклидовой плоскости, в которых любая точка лежит на трёх прямых и любая прямая содержит три точки), которые не изоморфны относительно отношения инцидентности конфигурации Дезарга, и одна из этих конфигураций показана на рисунке справа. Во всех этих конфигурациях для любой выбранной точки всегда существуют три других, не лежащих с ней на одной прямой и эти точки не лежат на одной прямой. В конфигурации же Дезарга эти три точки всегда лежат на одной прямой. Так, если выберем центр перспективы, то эти три точки лежат на оси перспективы. На примере же справа такие точки формируют треугольник. Как и в случае конфигурации Дезарга, другие конфигурации можно представить в виде пары взаимно вписанных друг в друга пятиугольников.

Примечания
  1. Barnes, 2012.
  2. Coxeter, 1964.
  3. Hilbert, Cohn-Vossen, 1952.

Литература
  • Barnes John. Gems of Geometry. — Springer, 2012. — С. 95–97. — ISBN 9783642309649.
  • H.S.M Coxeter. Projective Geometry. — New York: Blaisdell, 1964. — С. 26–27.
  • David Hilbert; Stephan Cohn-Vossen. Geometry and the Imagination. — 2nd. — Chelsea, 1952. — С. 119–128. — ISBN 0-8284-1087-9.
  • A. B. Kempe. A memoir on the theory of mathematical form // Philosophical Transactions of the Royal Society of London. — 1886. — Т. 177. — С. 1–70. — doi:10.1098/rstl.1886.0002.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.