Двойная шестёрка Шлефли

Двойная шестёрка Шлефли — это конфигурация из 30 точек и 12 прямых, предложенная Шлефли[1]. Прямые конфигурации можно разделить на два подмножества по 6 прямых, при этом каждая прямая не пересекается (то есть, скрещивается) с прямыми одного множества и пересекается с каждой прямой другого [кроме себя самой]). Каждая из 12 прямых конфигурации имеет 5 точек пересечения, и каждая из этих 30 точек пересечения принадлежит ровно двум прямым, принадлежащим разным подмножествам, так что двойная шестёрка Шлефли обозначается как 12₅30₂.

Построение

Как показал Шлефли, двойную шестёрку можно построить из любых пяти прямых a₁, a₂, a₃, a₄, a₅, если они пересекаются с шестой прямой b₆, но в остальном находятся в общем положении (в частности, каждая из двух прямых a_i и a_j должны скрещиваться, и никакие из четырёх прямых a_i не должны лежать на общей линейчатой поверхности). Для каждой из пяти прямых a_i дополнительное множество из прямых имеет две четверные секущие: b₆ и b_i. Пять прямых b₁, b₂, b₃, b₄ и b₅, полученные таким образом, пересекаются прямой a₆. Двенадцать прямых a_i и b_i образуют двойную шестёрку — каждая прямая a_i имеет пересечение с пятью прямыми b_j, для которых i ≠ j и наоборот.

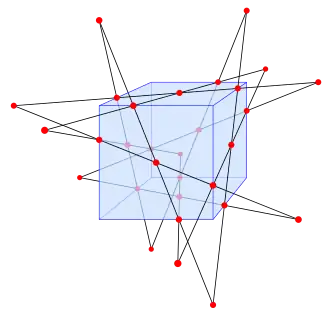
Другое построение, показанное на иллюстрации, получается путём расположения двенадцати прямых, проходящих через центры шести сторон куба и лежащих на плоскости этих сторон, и каждая прямая имеет один и тот же угол с соответствующими рёбрами куба.

Связанные объекты

Корона с 12 вершинами, граф пересечений прямых двойной шестёрки

В общем случае кубическая поверхность содержит 27 прямых, среди которых можно найти 36 конфигураций двойных шестёрок Шлефли. Множество из 15 прямых, дополнительное двойной шестёрке, вместе с 15 касательными плоскостями, проходящими через тройки этих прямых, имеет структуру пересечений другой конфигурации, конфигурации Кремоны — Ричмонда.

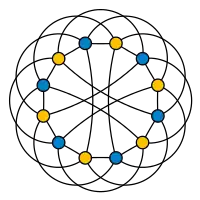
Граф пересечений двенадцати прямых конфигураций двойной шестёрки — это корона с 12 вершинами, двудольный граф, в котором каждая вершина смежна с пятью из шести вершин другого цвета. Граф Леви двойной шестёрки можно получить путём замены каждого ребра короны путём из двух рёбер. Граф пересечений всех 27 прямых на кубической поверхности является дополнением графа Шлефли.

Примечания

Schläfli, 1858, p. 115.

Литература

David Hilbert, Stephan Cohn-Vossen. Geometry and the Imagination. — 2nd. — New York: Chelsea, 1952. — ISBN 978-0-8284-1087-8.
Ludwig Schläfli. An attempt to determine the twenty-seven lines upon a surface of the third order, and to derive such surfaces in species, in reference to the reality of the lines upon the surface // Quarterly journal of pure and applied mathematics / Arthur Cayley. — 1858. — Т. 2. — С. 55–65, 110–120.

Ссылки

Weisstein, Eric W. Double Sixes (англ.) на сайте Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_6f7c09bbc75555d4-1] Schläfli, 1858, p. 115.