Линейчатая поверхность

• 
  Линейчатый геликоид
• 
  Линейчатый гиперболоид
• 
  Гиперболический параболоид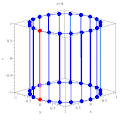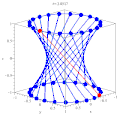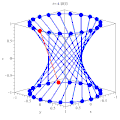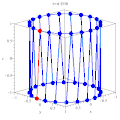
• 
  Цилиндр, гиперболоиды и конус как линейчатые поверхности

• Линейчатая поверхность характеризуется тем, что её асимптотическая сеть ― полугеодезическая.
• Гауссова кривизна линейчатой поверхности ${\displaystyle K\leq 0}$.
• Теорема Бельтрами. Линейчатую поверхность всегда можно и притом единственным образом изогнуть так, что произвольная линия на ней станет асимптотической.
• Теорема Бонне. Кроме того, если линейчатая поверхность ${\displaystyle F}$, не являющаяся развёртывающейся, изгибается в линейчатую поверхность ${\displaystyle F'}$, то либо их образующие соответствуют друг другу, либо обе они изгибаются в квадрику, на которой сеть, соответствующая семействам образующих, ― асимптотическая.
• Единственная минимальная линейчатая поверхность ― геликоид.
• Линейчатая поверхность вращения ― однополостный гиперболоид, может быть вырождающейся в цилиндр, конус или плоскость.
• Существуют примеры гладких линейчатых поверхностей, не допускающих гладких параметризаций вида

  ${\displaystyle r(u,v)=p(u)+v\cdot m(u).}$

• Поверхность Каталана — линейчатая поверхность, все прямолинейные образующие которой параллельны одной плоскости.
• Цилиндрическая поверхность — линейчатая поверхность, все прямолинейные образующие которой параллельны.
• Коноид — линейчатая поверхность, у которой образующие пересекают фиксированную прямую.

• 
  Синусоидальная линейчатая крыша, Храм Святого Семейства (Барселона)
• 
  Didcot power stations
• 
  Башня в Цехануве
• 
  Башня Кобе.
• 
  Первая Шуховская башня, 1896 Нижний Новгород.
• 
  Шуховская башня в Москве.
• 
  лестница в Торраццо Кремоны.
• 
  Параболическая крыша Варшава.
• 
  Коническая шапка.
• 
  Ротонда Св. Николая в Село, Словения

Поверхности, образованные движением геодезической в метрическом пространстве также называются линейчатыми поверхностями. Классический результат Александрa Даниловичa Александровa утверждает, что линейчатая поверхность в CAT(0) пространстве с индуцированной внутренней метрикой является CAT(0) пространством.[1]

• Линейчатые поверхности // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.