Граф пересечений
В теории графов графом пересечений называется граф, представляющий схему пересечений семейства множеств. Любой граф можно представить как граф пересечений, но некоторые важные специальные классы можно определить посредством типов множеств, используемых для представления в виде пересечений множеств.
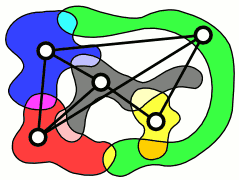
Обзор теории графов пересечений и важных специальных классов графов пересечений смотрите в книге МакКи и МакМорриса[1].
Формальное определение
Граф пересечений — это неориентированный граф, образованный из семейства множеств
путём создания вершины для каждого множества и соединения двух вершин и ребром, если соответствующие два множества имеют непустое пересечение, то есть
- .
Все графы являются графами пересечений
Любой неориентированный граф G можно представить как граф пересечений — для любой вершины графа G образуем множество , состоящее из рёбер, инцидентных . Два таких множества имеют непустое пересечение тогда и только тогда, когда соответствующие вершины принадлежат одному ребру. Эрдёш, Гудман и Поза[2] показали более эффективное построение (которое требует меньше элементов во всех множествах ), в котором общее число элементов в множествах не превосходит , где n — число вершин в графе. По их утверждению, что все графы являются графами пересечений, заметил Марчевский[3], но также рекомендовали посмотреть работы Чулика[4]. Число пересечений графа — это минимальное число элементов в представлениях графа, как графа пересечений.
Классы графов пересечений
Много важных семейств графов можно описать как графы пересечений ограниченных типов множеств, например, множеств, полученных из некоторых геометрических конфигураций:
- Интервальный граф определяется как граф пересечений интервалов на прямой, или связных подграфов-путей.
- Граф дуг окружности определяется как граф пересечений дуг окружности.
- Граф многоугольников на окружности определяется как граф пересечений многоугольников с вершинами, лежащими на окружности.
- Одна из характеристик хордальных графов — это то, что они являются графами пересечений связных подграфов дерева.
- Трапецеидальный граф определяется как граф пересечений трапеций, образованных двумя параллельными прямыми. Они являются обобщением понятия графа перестановки, которые, в свою очередь, являются специальным случаем семейства дополнений графов сравнимости, известных как графы косравнимости.
- Граф единичных кругов определяется как граф пересечений единичных кругов на плоскости.
- Теорема об упаковке кругов утверждает, что планарные графы — это в точности графы пересечений семейств замкнутых непересекающихся (разрешено касание) дисков на плоскости.
- Гипотеза Шейнермана (теперь — теорема) утверждает, что любой планарный граф можно представить в виде графа пересечений отрезков на плоскости. Однако графы пересечений отрезков на прямой могут быть непланарными, и распознавание графов пересечений отрезков на прямой является полным для теории существования вещественных чисел[5].
- Рёберный граф графа G определяется как граф пересечений рёбер графа G, где каждое ребро рассматривается как множество из двух его конечных вершин.
- Струнный граф — это граф пересечений кривых на плоскости.
- Граф имеет рамочность k, если он является графом пересечений многомерных прямоугольников размерности k, но не меньших размерностей.
Вариации и обобщения
- Теоретическими аналогами порядка графов пересечений служат порядки вложенности. Точно таким же образом, каким представление графа пересечений помечает каждую вершину множеством инцидентных ей рёбер, имеющих непустое пересечение, представление порядка вложенности f частично упорядоченного множества помечает каждый элемент таким множеством, что для любого x и y в нём тогда и только тогда, когда .
- Нерв покрытия
Примечания
Литература
- K. Čulík. Theory of Graphs and its Applications (Proc. Sympos. Smolenice, 1963). — Prague: Publ. House Czechoslovak Acad. Sci., 1964. — С. 13—20.
- Paul Erdős, A. W. Goodman, Louis Pósa. The representation of a graph by set intersections // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 106—112. — doi:10.4153/CJM-1966-014-3.
- Martin Charles Golumbic. Algorithmic Graph Theory and Perfect Graphs. — Academic Press, 1980. — ISBN 0-12-289260-7.
- Topics in Intersection Graph Theory. — Philadelphia: Society for Industrial and Applied Mathematics, 1999. — Т. 2. — (SIAM Monographs on Discrete Mathematics and Applications). — ISBN 0-89871-430-3.
- E. Szpilrajn-Marczewski. Sur deux propriétés des classes d'ensembles // Fund. Math.. — 1945. — Т. 33. — С. 303—307.
- Marcus Schaefer. Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers. — Springer-Verlag, 2010. — Vol. 5849. — С. 334—344. — (Lecture Notes in Computer Science). — ISBN 978-3-642-11804-3. — doi:10.1007/978-3-642-11805-0_32.
Ссылки
- Jan Kratochvíl, A video lecture on intersection graphs (June 2007)
- E. Prisner, A Journey through Intersection Graph County
