Граф многоугольников на окружности

В теории графов графом многоугольников на окружности или паутиной называется граф пересечений, в котором каждая вершина соответствует многоугольнику с вершинами, лежащими на окружности, а рёбра, соединяющие две вершины графа, задаются пересечением двух многоугольников, соответствующих этим вершинам. Графы многоугольников на окружности предложены впервые в 1988 году Михаэлем Феллоузом.

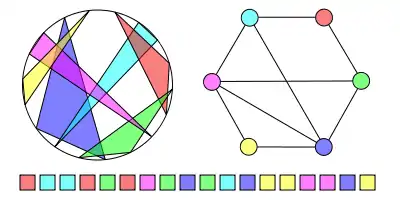
Слева — множество многоугольников, вписанных в окружность. Справа — соответствующий граф многоугольников на окружности (граф пересечений многоугольников). Внизу — чередующаяся последовательность многоугольников по окружности.

Граф многоугольников на окружности можно задать «чередующейся последовательностью». Такую последовательность можно получить разорвав окружность в произвольном месте и перечислив вершины многоугольников, идя вдоль окружности. Такая последовательность единственна.

Распознавание

М. Кёбе (M. Koebe) объявил об алгоритме распознавания графа за полиномиальное время[1], но этот алгоритм нигде не был опубликован. Такой алгоритм впервые опубликовали Пергель (M. Pergel) и Краточвил (J. Kratochvíl)[2].

Примечания
  1. M. Koebe. On a new class of intersection graphs // Proceedings of the Fourth Czechoslovak Symposium on Combinatorics Prachatice. — 1990. — P. 141—143.
  2. M. Pergel. Special Graph Classes and Algorithms on Them. Doctoral Thesis, 2007.

Литература
  • J. P. Spinrad. Efficient Graph Representations. American Mathematical Society, 2003.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.