Гипотеза Шейнермана
Гипотеза Шейнермана[1], теперь доказанная теорема, утверждает, что любой планарный граф является графом пересечений набора отрезков на плоскости. Эту гипотезу сформулировал Эдвард Шейнерман в своей кандидатской диссертации[2], следуя более раннему результату, что любой планарный граф можно представить как граф пересечений простых кривых на плоскости[3]. Теорему доказали Чалопин и Гонсалвис[4].
Пример
Например, граф G, показанный ниже слева может быть представлен как граф пересечений набора отрезков, показанных справа. Здесь вершины графа G представлены отрезками, а рёбра графа G представлены точками пересечений этих отрезков.
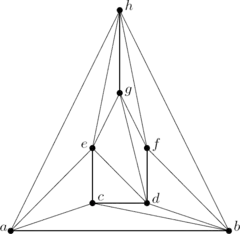
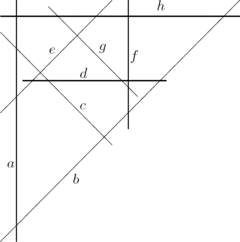
Развитие
Шейнерман также высказал гипотезу, что достаточно иметь отрезки трёх направлений для представления раскрашиваемых в 3 цвета графов, а Вест[5] высказал гипотезу, что, аналогично, любой планарный граф может быть представлен с помощью отрезков четырёх направлений. Если граф представим отрезками, имеющими только k направления, и никакие два отрезка не лежат на одной прямой, граф можно выкрасить с помощью k цветов, по одному цвету на каждое направление. Поэтому, если любой планарный граф может быть представлен таким способом только с четырьмя направлениями отрезков, отсюда будет следовать теорема о четырёх красках.
Хартман, Ньюман и Зив[6], а также Де Фрейсикс, Оссона де Мендез и Пах[7], доказали, что любой двудольный планарный граф может быть представлен как граф пресечений горизонтальных и вертикальных отрезков. См. об этом статью Чижовича, Кранакиса и Уррутия[8]. Де Кастро, Кобос, Дана и Маркес[9] доказали, что любой свободный от треугольников планарный граф может быть представлен как граф пересечений отрезков, имеющих всего три направления. Из их результата вытекает теорема Грёча[10], что свободные от треугольников планарные графы могут быть раскрашены в три цвета. Де Фрейсикс и Оссона де Мендез[11] доказали, что если планарный граф G может быть раскрашен в 4 цвета так, что никакой разделяющий цикл не использует все четыре цвета, то граф G имеет представление как граф пересечений отрезков.
Струнные графы
Чалопин, Гонсалвис и Очем[12] доказали, что планарные графы находятся в классе 1-СТРУН, классе графов пересечений простых кривых на плоскости, которые пересекают друг друга максимум один раз на пару кривых. Этот класс является средним между графами пересечений отрезков, появляющихся в гипотезе Шейнерман, и графами пересечений простых кривых без ограничений из результатов Эрлиха (и его соавторов). Гипотезу можно рассматривать как обобщение теоремы об упаковке кругов, которая даёт тот же результат, когда кривые могут только касаться друг друга. Доказательство гипотезы, которое дали Чалопин и Гонсалвис[4] базировалось на улучшении этого результата.
Примечания
- Фамилия немецкого происхождения и на немецком она должна звучать Шайнерман, однако данный математик из США.
- Scheinerman, 1984.
- Ehrlich, Even, Tarjan, 1976.
- Chalopin, Gonçalves, 2009.
- West, 1991.
- Hartman, Newman, Ziv, 1991.
- de Fraysseix, Ossona de Mendez, Pach, 1991.
- Czyzowicz, Kranakis, Urrutia, 1998.
- De Castro, Cobos, Dana, Márquez, 2002.
- Grötzsch, 1959.
- de Fraysseix, Ossona de Mendez, 2005.
- Chalopin, Gonçalves, Ochem, 2007.
Литература
- De Castro N., Cobos F. J., Dana J. C., Márquez A. Triangle-free planar graphs as segment intersection graphs // Journal of Graph Algorithms and Applications. — 2002. — Т. 6, вып. 1. — С. 7–26. — doi:10.7155/jgaa.00043.
- Chalopin J., Gonçalves D. ACM Symposium on Theory of Computing. — 2009.
- Chalopin J., Gonçalves D., Ochem P. Planar graphs are in 1-STRING // Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. — ACM and SIAM, 2007. — С. 609–617.
- Czyzowicz J., Kranakis E., Urrutia J. A simple proof of the representation of bipartite planar graphs as the contact graphs of orthogonal straight line segments // Information Processing Letters. — 1998. — Т. 66, вып. 3. — С. 125–126. — doi:10.1016/S0020-0190(98)00046-5.
- de Fraysseix H., Ossona de Mendez P. Graph Drawing, 12th International Symposium, GD 2004. — Springer-Verlag, 2005. — Т. 3383. — С. 217–227. — (Lecture Notes in Computer Science).
- de Fraysseix H., Ossona de Mendez P., Pach J. Representation of planar graphs by segments // Intuitive Geometry. — 1991. — Т. 63. — С. 109–117.
- Ehrlich G., Even S., Tarjan R. E. Intersection graphs of curves in the plane // Journal of Combinatorial Theory. — 1976. — Т. 21, вып. 1. — С. 8–20. — doi:10.1016/0095-8956(76)90022-8.
- Herbert Grötzsch. Zur Theorie der diskreten Gebilde, VII: Ein Dreifarbensatz für dreikreisfreie Netze auf der Kugel // Wiss. Z. Martin-Luther-U., Halle-Wittenberg, Math.-Nat. Reihe. — 1959. — Т. 8. — С. 109–120.
- Hartman I. B.-A., Newman I., Ziv R. On grid intersection graphs // Discrete Mathematics. — 1991. — Т. 87, вып. 1. — С. 41–52. — doi:10.1016/0012-365X(91)90069-E.
- Scheinerman E. R. Intersection Classes and Multiple Intersection Parameters of Graphs. — Princeton University, 1984. — (Ph.D. thesis).
- West D. Open problems #2 // SIAM Activity Group Newsletter in Discrete Mathematics. — 1991. — Т. 2, вып. 1. — С. 10–12.