Теорема об упаковке кругов

Граф G называется триангулированным планарным (или максимальным планарным), если он планарен и любая связная компонента дополнения вложения G в сферу имеет ровно три ребра на границе, или, другими словами, если G является одномерным остовом симплициального комплекса, который гомеоморфен сфере. Любой триангулированный планарный граф G является связным и простым, поэтому теорема об упаковке кругов гарантирует существование упаковки, граф касаний которой изоморфен G. Такой граф G должен быть конечным, так что соответствующая упаковка будет иметь конечное число кругов. Как утверждает следующая теорема, любой максимальный планарный граф может соответствует не более чем одной упаковке.

Теорема Кёбе — Андреева — Тёрстона: если G является конечным триангулированным планарным графом, то упаковка кругов, граф касания которой равен (изоморфен) G, единственна с точностью до преобразований Мёбиуса и отражений относительно прямых.

Тёрстон[1] заметил, что эта единственность является следствием теоремы Мостова о жёсткости. Плоскость, в которой круги упакованы, можно рассматривать как границу модели Пуанкаре в полупространстве. С этой точки зрения, любой круг является границей плоскости в гиперболическом пространстве. Каждой упаковке кругов можно сопоставить множество непересекающихся плоскостей, а также второе множество непересекающихся плоскостей, определённых треугольными участками между тремя кругами упаковки. Плоскости из различных множеств пересекаются под прямыми углами и соответствуют генераторам группы отражений, фундаментальную область которой можно рассматривать как гиперболическое многообразие. По теореме о жёсткости Мостова, гиперболическая структура этой области определена однозначно с точностью до изометрий гиперболического пространства. Эти изометрии, если рассматривать их в терминах действия на границе модели Пуанкаре, превращаются в преобразования Мёбиуса.

Существует также элементарное доказательство, основанное на принципе максимума и на том наблюдении, что в треугольнике, соединяющем центры трёх взаимно касающихся окружностей, угол, образованный в вершине в центре одной из окружностей монотонно уменьшается при увеличении её радиуса и монотонно возрастает при увеличении любого из двух других радиусов. Если даны две упаковки для того же самого графа G, можно использовать отражения и преобразования Мёбиуса, чтобы сделать внешние круги в этих двух упаковках соответствующими друг другу и имеющими одинаковые радиусы. Тогда, пусть v — внутренняя вершина графа G, для которой круги в двух упаковках имеют размеры, как можно более далёкие друг от друга. То есть, выбирается v так, чтобы максимизировать отношение r₁/r₂ радиусов кругов этих двух упаковок. Отсюда следует, что для каждой треугольной грани графа G, содержащей v, угол с вершиной центра круга, соответствующий v в первой упаковке меньше или равен углу во второй упаковке, с равенством только в случае, когда два других круга образуют треугольник с тем же отношением r₁/r₂ радиусов второй упаковки. Но сумма углов всех треугольников, окружающих центр треугольника, должен быть равен 2π в обоих упаковках, так что все соседние v вершины должны иметь то же самое отношение, что и у самого v. Применяя те же рассуждения к другим кругам, получается, что все круги в обеих упаковках имеют то же самое отношение. Но внешние круги трансформированы так, чтобы иметь отношение 1, так что r₁/r₂ = 1 и обе упаковки имеют равные радиусы для всех кругов.

Упаковку кругов можно обобщить для графов, не являющихся планарными.

Если G является графом, который может быть вложен в ориентируемую поверхность S, то на S существует риманова метрика d постоянной кривизны и упаковка кругов в (S, d), граф касаний которого изоморфен G. Если S замкнута (компактна и не имеет границы) и G — триангуляция S, то (S, d) и упаковка единственны с точностью до конформной эквивалентности. Если S — сфера, то конформная эквивалентность — это эквивалентность с точностью до преобразований Мёбиуса; если это тор, то с точностью до умножения на константу и изометрии; в случае если род поверхности не меньше 2 — с точностью до изометрии.

Другое обобщение теоремы об упаковке кругов вовлекает замену условия касания указанием угла пересечения между окружностями, соответствующих соседним вершинам. В частности, имеется следующая элегантная версия этой теоремы. Предположим, что G является конечным 3-связным плоским графом (другими словами, полиэдральным графом), тогда существует пара упаковок кругов, таких что граф пересечений одной упаковки изоморфен G, а граф пересечений другой изоморфен планарному двойственному G графу. При этом для любой вершины в G и грани, смежной ей, соответствующая вершине окружность в первой упаковке пересекается под прямым углом с окружностью, соответствующий грани во второй упаковке[2]. Например, применение этого результата к графу тетраэдра даёт для любых четырёх попарно касающихся окружностей второе множество четырёх взаимно касательных окружностей, каждая из которых ортогональна трём из первого набора [3]. Дальнейшее обобщение можно получить заменой угла пересечения инверсным расстоянием[4].

Ещё одно обобщение позволяет использовать фигуры, отличные от кругов. Предположим, что G = (V, E) является конечным планарным графом, и каждая вершина v графа G соответствует фигуре ${\displaystyle K_{v}\subset \mathbb {R} ^{2}}$, которая гомеоморфна замкнутому единичному диску и граница которой гладкая. Тогда существует упаковка ${\displaystyle P=(K'_{v}:v\in V)}$ на плоскости, такая что ${\displaystyle K'_{v}\cap K'_{u}\neq \varnothing }$ тогда и только тогда, когда ${\displaystyle [v,u]\in E}$ и для каждого ${\displaystyle v\in V}$ множество ${\displaystyle K'_{v}}$ получается из ${\displaystyle K_{v}}$ путём движения и масштабирования. (Заметим, что в исходной теореме об упаковке кругов имеется три параметра для вершины, два из которых задают центр соответствующей окружности и один задаёт радиус, и имеется одно уравнение для каждого ребра. Это выполняется и для этого обобщения.) Одно из доказательств этого обобщения можно получить путём использования исходного доказательства Коебе[5] и теоремы Брандта[6] и Харрингтона[7], утверждающего, что любая конечная связная область конформно эквивалентна плоской области, границы компонентов которой имеют специфичные фигуры с точностью до переноса и масштабирования.

Упаковки кругов можно использовать для приближения конформного отображения между областями. Каждый круг слева соответствует кругу справа.

Конформное отображение между двумя открытыми подмножествами плоскости или пространства более высокой размерности является непрерывным и сохраняет углы между любыми двумя кривыми. Теорема Римана об отображении, сформулированная Риманом в 1851 году, утверждает, что для любых двух открытых топологических дисков на плоскости существует конформное отображение из одного диска в другой.

Конформные отображения имеют приложения в построении расчётных сеток, картографических проекций и других областях. Однако не всегда просто построить конформное отображение между двумя заданными областями явным образом[8].

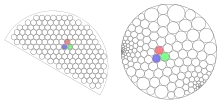
На конференции в 1985 году Уильям Тёрстон высказал предположение, что упаковку кругов можно было бы использовать для аппроксимации конформных отображений. Точнее, Тёрстон использовал упаковки кругов для поиска конформного отображения произвольного открытого (топологического) диска A во внутренность круга. Отображение из топологического диска в другой диск B можно найти тогда суперпозицией отображения из A в круг и отображения, обратного отображению B в круг[9].

Идея Тёрстона заключалась в том, чтобы построить упаковку кругов некоторого маленького радиуса r в виде шестиугольной мозаики[10] на плоскости внутри области A, оставляя узкую полосу около границы A, в которой нельзя разместить ещё один круг этого радиуса. Затем по графу пересечений кругов строится максимальный планарный граф G и добавляется одна дополнительная вершина, смежную всем окружностям на границе упаковки. По теореме об упаковке кругов этот планарный граф может быть представлен упаковкой кругов C, в которой все рёбра (включая рёбра, инцидентные граничным вершинам) представлены касаниями кругов. Круги из упаковки A взаимно-однозначно соответствуют кругам из C, за исключением граничной окружности C, которая соответствует границе A. Это соответствие может быть использовано для построения непрерывного отображения из A в C, при котором каждый круг и каждый промежуток между тремя кругами отображается из одной упаковки в другую при помощи преобразования Мёбиуса. Тёрстон предположил, что при стремлении радиуса r к нулю отображение из A в C, построенное таким образом, стремится к конформной функции, которую даёт теорема Римана[9].

Гипотеза Тёрстона доказана Родином и Салливаном[11]. Точнее, они показали, что при стремлении n к бесконечности функция f_n, получаемая с помощью метода Тёрстона, из упаковки кругами радиуса 1/n сходится равномерно на компактных подмножествах A к конформному отображению из A в C[9].

Несмотря на подтверждение гипотезы Тёрстона, практическое применение этого метода затруднено сложностью построения упаковок кругами и относительно медленной сходимостью. Тем не менее, этот метод можно успешно использовать в случае неодносвязных областей и при выборе начальных приближений для численных методов, которые вычисляют отображения Шварца — Кристоффеля — несколько отличный метод для построения конформных отображений многоугольных областей[9].

Многогранник полувписанной сферой. Из теоремы об упаковке кругов следует, что любой полиэдральный граф может быть представлен как граф многогранника, имеющего полувписанную сферу.

Теорема об упаковке кругов является полезным средством для изучения различных задач планиметрии, конформных отображений и планарных графов. Элегантное доказательство теоремы о разбиении в планарном графе, первоначально доказанной Липтоном и Тарьяном[12], получено при помощи теоремы об упаковке кругов[13]. Другим применением теоремы об упаковке кругов является доказательство утверждения, что несмещённые пределы планарных графов с ограниченной степенью почти всегда рекурсивны[14].

Другие применения — выводы для времени случайного обхода графа[15] и оценка максимального собственного значения графов с ограниченным родом [16].

При визуализации графов упаковка кругов используется для нахождения представления планарного графа с ограниченным разрешением[17] и с ограниченным числом наклонов[18].

Вычисление радиуса окружности (выделена красным) радиуса r₀.
На первом шаге вычисляем угол θ.
На втором шаге вычисляем усреднённый радиус r_s.
На третьем шаге вычисляем исправленный радиус окружности r_n

Существует множество известных доказательств теоремы об упаковке кругов. Оригинальное доказательство Пола Кёбе основывается на его теореме конформной параметризации, утверждающей, что конечно связная область конформно эквивалентна кругу. Существует несколько различных известных топологических доказательств. Доказательство Тёрстона основывается на теореме Брауэра о неподвижной точке.

Существует также доказательство, использующее дискретный вариант метода Перрона построения решения задачи Дирихле. Ивз Колин де Вердьер (Yves Colin de Verdière) доказал[19] существование упаковки кругов как минимизатора выпуклой функции на некоторых пространствах конфигураций.

Теорема Фари, утверждающая что любой граф, который может быть представлен без пересечений на плоскости с использованием кривых рёбер, может быть также нарисован без пересечений с помощью отрезков, является простым следствием теоремы об упаковке кругов — разместив вершины в центрах кругов и проведя отрезки, соединяющие соприкасающиеся окружности, получим представление с рёбрами в виде отрезков.

Строгий вариант теоремы об упаковке утверждает, что любой полиэдральный граф и его двойственный граф могут быть представлены двумя упаковками кругов, таких, что две касающихся окружности, представляющие ребро основного графа, и две других касающихся окружности, представляющие ребро двойственного графа, пересекаются под прямым углом. Упаковка такого типа может быть использована для построения выпуклого многогранника, представляющено заданный граф и имеющего полувписанную сферу, сферу, касающуюся всех рёбер многогранника. Обратно, если многогранник имеет полувписанную сферу, то окружности, образованные пересечением сферы с гранями многогранника, и окружности, образованные горизонтами сферы, которые видны из вершин многогранника, образуют двойственные упаковки.

Коллинз и Стефенсон [20] описали численный релаксационный алгоритм для нахождения упаковок окружностей, основанный на идеях Уильяма Тёрстона. Версия задачи упаковки кругов, которую они решают, имеет на входе планарный граф, в котором все внутренние грани являются треугольниками и все внешние вершины помечены положительными числами. Алгоритм даёт упаковку кругов, точки касания которых представляют заданный граф и для которого круги, представляющие внешние вершины, имеют заданный во входе радиус. Как они предположили, ключ к проблеме лежит в первоначальном вычислении радиусов кругов упаковки. Если радиусы известны, геометрические положения кругов нетрудно вычислить. Они начинают с пробных радиусов, которые не соответствуют реальным упаковкам, а потом в цикле выполняют следующие шаги:

1. Выберем внутреннюю вершину входного графа, эта вершина соответствует некоторой окружности, которую будем обозначать v. Соседние вершины соответствуют лепесткам, то есть окружностям, касающимся выбранной окружности. Пусть k — число лепестков.
2. Вычисляем полный угол θ, который перекрывается k соседними окружностями около окружности v, если их разместить вплотную друг другу и которые касаются центральной окружности.
3. Вычисляем усреднённый радиус r_s для лепестков, такой что k окружностей радиуса r_s перекрывают тот же самый угол θ, какой дают соседи v.
4. Устанавливаем новый радиус r_n для v, такой что k окружностей усреднённого радиуса перекрывали бы в точности 2π.

Каждый из этих шагов можно выполнить с помощью простых тригонометрических вычислений, и как указали Коллинз и Стефенсон (Collins, Stephenson), система радиусов сходится к единственной неподвижной точке, для которой все покрывающие углы равны 2π. После того, как система радиусов сошлась, окружности можно разместить по одной, на каждом шаге используя положение и радиусы двух соседних окружностей для вычисления центра каждой успешной окружности.

Мохар[21] описывает похожую итеративную технику для поиска упаковок полиэдрального графа и его двойственного, в которых двойственные циклы пересекаются под прямым углом с основными окружностями. Он доказал, что метод работает за полиномиальное от числа окружностей время и от log 1/ε, где ε является границей расстояний от центров и разницей радиусов вычисленной упаковки и оптимальной упаковки.

Теорема об упаковке кругов впервые доказана Паулем Кёбе[5].

Уильям Тёрстон[1] переоткрыл теорему об упаковке кругов и заметил, что она следует из работы Е. М. Андреева. Тёрстон также предложил схему использования теоремы об упаковке кругов для получения гомеоморфизма связного множества на плоскости во внутреннюю область единичного круга. Гипотеза Тёрстона об упаковке кругов — это предположение, что гомеоморфизм сходится к отображению Римана при стремлении радисов к нулю. Гипотезу Тёрстона позднее доказали Бёртон Родин и Деннис Салливан[11]. Это привело к многочисленным исследованиям по обобщению теоремы об упаковке окружностей, а также исследованиям по связям с конформными отображениями и приложениям теоремы.

• Упаковка кругов в круге
• Задачи упаковки
• Упаковка шаров
• Сетка Аполлония, вид планарного графа, определённого из упаковки окружностей.

• Е. М. Андреев. О выпуклых многогранниках в пространствах Лобачевского // Матем. сб. — 1970. — Т. 81(123), вып. 3. — С. 445—478.
• Е. М. Андреев. О выпуклых многогранниках конечного объёма в пространстве Лобачевского // Матем. сб.. — 1970. — Т. 83(125), вып. 2(10). — С. 256—260.
• Itai Benjamini, Oded Schramm. Recurrence of distributional limits of finite planar graphs // Electronic Journal of Probability. — 2001. — Т. 6.
• Philip L. Bowers, Kenneth Stephenson. 8.2 Inversive distance packings // Uniformizing dessins and Belyĭ maps via circle packing. — 2004. — Т. 805. — С. 78—82. — (Memoirs of the American Mathematical Society). — doi:10.1090/memo/0805.
• M. Brandt. Ein Abbildungssatz fur endlich-vielfach zusammenhangende Gebiete // Bull. de la Soc. des Sc. et des Lettr. de Łódź. — 1980. — Т. 30.
• H. S. M. Coxeter. Non-Euclidean geometries. — New York: Springer, 2006. — Т. 581. — (Math. Appl. (N. Y.)). — doi:10.1007/0-387-29555-0_5.
• Graham R. Brightwell, Edward R. Scheinerman. Representations of planar graphs // SIAM J. Discrete Math. — 1993. — Т. 6, вып. 2. — doi:10.1137/0406017.
• Yves Colin de Verdière. Une principe variationnel pour les empilements de cercles // Inventiones Mathematicae. — 1991. — Т. 104, вып. 1. — doi:10.1007/BF01245096.
• Charles R. Collins, Kenneth Stephenson. A circle packing algorithm // Computational Geometry. Theory and Applications. — 2003. — Т. 25, вып. 3. — doi:10.1016/S0925-7721(02)00099-8.
• Andrew N. Harrington. Conformal mappings onto domains with arbitrarily specified boundary shapes // Journal d'Analyse Mathématique. — 1982. — Т. 41, вып. 1. — doi:10.1007/BF02803393.
• Johan Jonnason, Oded Schramm. On the cover time of planar graphs // Electronic Communications in Probability. — 2000. — Т. 5. — С. 85—90.
• Jonathan A. Kelner. Spectral partitioning, eigenvalue bounds, and circle packings for graphs of bounded genus // SIAM Journal on Computing. — 2006. — Т. 35, вып. 4. — doi:10.1137/S0097539705447244.
• Balázs Keszegh, János Pach, Dömötör Pálvölgyi. Drawing planar graphs of bounded degree with few slopes // Graph Drawing: 18th International Symposium, GD 2010, Konstanz, Germany, September 21—24, 2010, Revised Selected Papers / Ulrik Brandes, Sabine Cornelsen,. — Heidelberg: Springer, 2011. — Т. 6502. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-18469-7_27.
• Paul Koebe. Kontaktprobleme der Konformen Abbildung // Ber. Sächs. Akad. Wiss. Leipzig, Math.-Phys. Kl. — 1936. — Т. 88.
• Richard J. Lipton, Robert E. Tarjan. A separator theorem for planar graphs // SIAM Journal on Applied Mathematics. — 1979. — Т. 36. — С. 177–189. — doi:10.1137/0136016.
• Seth Malitz, Achilleas Papakostas. On the angular resolution of planar graphs // SIAM Journal on Discrete Mathematics. — 1994. — Т. 7, вып. 2. — doi:10.1137/S0895480193242931.
• Gary L. Miller, Shang-Hua Teng, William Thurston, Stephen A. Vavasis. Separators for sphere-packings and nearest neighbor graphs // J. ACM. — 1997. — Т. 44, вып. 1. — doi:10.1145/256292.256294.
• Bojan Mohar. A polynomial time circle packing algorithm // Discrete Mathematics. — 1993. — Т. 117, вып. 1—3. — doi:10.1016/0012-365X(93)90340-Y.
• Burton Rodin, Dennis Sullivan. The convergence of circle packings to the Riemann mapping // Journal of Differential Geometry. — 1987. — Т. 26, вып. 2.
• Kenneth Stephenson. The approximation of conformal structures via circle packing // Computational methods and function theory 1997 (Nicosia). — World Sci. Publ., River Edge, NJ, 1999. — Т. 11. — (Ser. Approx. Decompos.). Архивная копия от 21 мая 2012 на Wayback Machine
• Ken Stephenson. Introduction to circle packing, the theory of discrete analytic functions. — Cambridge: Cambridge University Press, 2005.
• William Thurston. The finite Riemann mapping theorem. — 1985. — (Invited talk at the International Symposium at Purdue University on the occasion of the proof of the Bieberbach conjecture).
• William Thurston. The geometry and topology of 3-manifolds. — Princeton lecture notes, 1978—1981.
• Kenneth Stephenson. Circle Packing: A Mathematical Tale // Notices of the AMS. — Т. 50, вып. 11. — С. 1376—1388.

• CirclePack (free software for constructing circle packings from graphs)
• Circle packing bibliography by Kenneth Stephenson, Univ. of Tennessee