Упаковка кругов в правильном треугольнике
Задача упаковки кругов в правильный треугольник — это задача упаковки, в которой требуется упаковать n единичных окружностей в наименьший правильный треугольник. Оптимальные решения известны для n < 13 и для любого треугольного числа кругов. Имеются гипотезы для числа кругов n < 28[1][2][3].
Гипотеза Пала Эрдёша и Нормана Олера утверждает, что в случае, когда n является треугольным числом, оптимальная упаковка n − 1 и n кругов имеет одну и ту же длину стороны. То есть, согласно гипотезе, оптимальное решение для n − 1 кругов можно получить путём удаление одного круга из оптимальной шестиугольной упаковки n кругов[4][5].
Минимальные по длине стороны треугольника решения[1]:
| Число кругов | Длина стороны треугольника |
|---|---|
| 1 | = 3.464... |
| 2 | = 5.464... |
| 3 | = 5.464... |
| 4 | = 6.928... 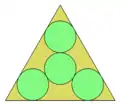 |
| 5 | = 7.464... 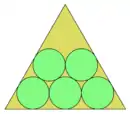 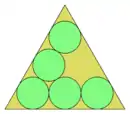 |
| 6 | = 7.464... |
| 7 | = 8.928... |
| 8 | = 9.293... |
| 9 | = 9.464... |
| 10 | = 9.464... |
| 11 | = 10.730... |
| 12 | = 10.928... |
| 13 | = 11.406... |
| 14 | = 11.464... |
| 15 | = 11.464... |
Близкая задача — покрытие правильного треугольника заданным числом кругов с как можно меньшим радиусом[6].
См. также
- Упаковка кругов в прямоугольном равнобедренном треугольнике
- Окружности Мальфатти, построение, дающее оптимальное решение для трёх кругов в равнобедренном треугольнике
Примечания
- Melissen, 1993, с. 916–925.
- Melissen, Schuur, 1995, с. 333–342.
- Graham, Lubachevsky, 1995, с. 39 Article 1.
- Oler, 1961, с. 153–155.
- Payan, 1997, с. 555–565.
- Nurmela, 2000, с. 241–250.
Литература
- Hans Melissen. Densest packings of congruent circles in an equilateral triangle // The American Mathematical Monthly. — 1993. — Т. 100, вып. 10. — С. 916–925. — doi:10.2307/2324212.
- J. B. M. Melissen, P. C. Schuur. Packing 16, 17 or 18 circles in an equilateral triangle // Discrete Mathematics. — 1995. — Т. 145, вып. 1-3. — С. 333–342. — doi:10.1016/0012-365X(95)90139-C.
- Ronald Graham, B. D. Lubachevsky. Dense packings of equal disks in an equilateral triangle: from 22 to 34 and beyond // Electronic Journal of Combinatorics. — 1995. — Т. 2. — С. Article 1, approx. 39 pp. (electronic).
- Norman Oler. A finite packing problem // Canadian Mathematical Bulletin. — 1961. — Т. 4. — С. 153–155. — doi:10.4153/CMB-1961-018-7.
- Charles Payan. Empilement de cercles égaux dans un triangle équilatéral. À propos d'une conjecture d'Erdős-Oler (Fr) // Discrete Mathematics. — 1997. — Т. 165/166. — С. 555–565. — doi:10.1016/S0012-365X(96)00201-4.
- Kari J. Nurmela. Conjecturally optimal coverings of an equilateral triangle with up to 36 equal circles // Experimental Mathematics. — 2000. — Т. 9, вып. 2. — С. 241–250. — doi:10.1080/10586458.2000.10504649.
