Однородные мозаики на гиперболической плоскости
В гиперболической геометрии однородная (правильная, квазиправильная или полуправильная) гиперболическая мозаика — это заполнение гиперболической плоскости правильными многоугольниками ребро-к-ребру со свойством вершинной транзитивности (это мозаика транзитивная относительно вершин, изогональная, т.е. существует движение, переводящее любую вершину в любую другую). Отсюда следует, что все вершины конгруэнтны и мозаика имеет высокую степень вращательной и трансляционной симметрии.
| Сферическая | Евклидова | Гиперболические | |
|---|---|---|---|
 {5,3} 5.5.5 |
 {6,3} 6.6.6 |
 {7,3} 7.7.7 |
 {∞,3} ∞.∞.∞ |
| Правильные мозаики на сфере {p,q}, евклидовой плоскости и гиперболической плоскости с гранями в виде правильных пятиугольников, шестиугольников, семиугольников и бесконечноугольников. | |||
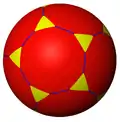 t{5,3} 10.10.3 |
 t{6,3} 12.12.3 |
 t{7,3} 14.14.3 |
 t{∞,3} ∞.∞.3 |
| Усечённые мозаики имеют вершинные фигуры 2p.2p.q, полученные из правильных {p,q} | |||
 r{5,3} 3.5.3.5 |
 r{6,3} 3.6.3.6 |
 r{7,3} 3.7.3.7 |
 r{∞,3} 3.∞.3.∞ |
| Квазиправильные мозаики подобны правильным мозаикам, но имеют два типа правильных многоугольников, поочерёдно следующих вокруг каждой вершины. | |||
 rr{5,3} 3.4.5.4 |
 rr{6,3} 3.4.6.4 |
 rr{7,3} 3.4.7.4 |
 rr{∞,3} 3.4.∞.4 |
| Полуправильные мозаики имеют более одного типа правильных многоугольников. | |||
 tr{5,3} 4.6.10 |
 tr{6,3} 4.6.12 |
 tr{7,3} 4.6.14 |
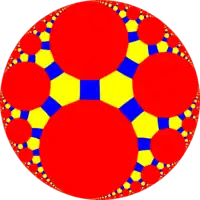 tr{∞,3} 4.6.∞ |
| Всеусечённые мозаики имеют три и более правильных многоугольников с чётным числом сторон. | |||
Однородные мозаики однозначно определяются их вершинной конфигурацией, последовательностью чисел, представляющих число сторон многоугольников вокруг каждой вершины. Например, 7.7.7 представляет семиугольную мозаику, имеющую 3 семиугольника вокруг каждой вершины. Она правильна, поскольку все многоугольники имеют один размер. Таким образом, её можно задать символом Шлефли {7,3}.
Однородные мозаики могут быть правильными (если они также транзитивны по граням и рёбрам), квазиправильными (если они рёберно транзитивны, но не транзитивны по граням) или полуправильными (если они не транзитивны ни по рёбрам, ни по граням). Для правильных треугольников (p q 2) существуют две правильные мозаики с символами Шлефли {p,q} и {q,p}.
Построение Витхоффа

Существует бесконечное число однородных мозаик, основанных на треугольниках Шварца (p q r), где 1/p + 1/q + 1/r < 1, где p, q, r являются порядками отражательной симметрии в трёх вершинах фундаментального треугольника – группа симметрии является гиперболической группой треугольника.
Каждое семейство симметрий содержит 7 однородных мозаик, определённых символом Витхоффа или диаграммой Коксетера — Дынкина, 7 комбинаций трёх активных зеркал. 8-я мозаика представляет операцию альтернации, удаления половины вершин из высшей формы активных зеркал.
Семейства с r = 2 содержат правильные гиперболические мозаики, определённые группами Коксетера, такими как [7,3], [8,3], [9,3], ... [5,4], [6,4], ....
Гиперболические семейства с r = 3 и выше задаются символами (p q r) и включают (4 3 3), (5 3 3), (6 3 3) ... (4 4 3), (5 4 3), ... (4 4 4)....
Гиперболические семейства (p q r) определяют компактные однородные гиперболические мозаики. В пределе любое из чисел p, q или r можно заменить символом ∞, что даёт паракомпактный гиперболический треугольник и создаёт однородные мозаики, имеющие либо бесконечные грани (назывемые апейрогонами или бесконечноугольниками), которые сходятся к одной воображаемой точке, либо бесконечные вершинные фигуры с бесконечным числом рёбер, исходящих из одной воображаемой точки.
Можно построить дополнительные семейства симметрий из фундаментальных областей, не являющихся треугольными.
Некоторые семейства однородных мозаик показаны ниже (с использованием модели Пуанкаре для гиперболической плоскости). Три из них – (7 3 2), (5 4 2) и (4 3 3) – и никакие другие, минимальны в том смысле, что если любое из определяющих чисел заменить на меньшее целое значение, получим либо евклидову, либо сферическую мозаику, а не гиперболическую. И обратно, любое из чисел можно увеличить (даже заменив на бесконечность), чтобы получить другой гиперболический узор.
Каждая однородная мозаика образует двойственную однородную мозаику, и многие из них приведены ниже также.
Прямоугольные фундаментальные треугольники
Существует бесконечно много семейств групп треугольника (p q 2). В статье показаны правильные мозаики вплоть до p, q = 8 и однородные мозаики 12 семейств: (7 3 2), (8 3 2), (5 4 2), (6 4 2), (7 4 2), (8 4 2), (5 5 2), (6 5 2) (6 6 2), (7 7 2), (8 6 2) и (8 8 2).
Правильные гиперболические мозаики
Простейшее множество гиперболических мозаик — правильные мозаики {p,q}. Правильная мозаика {p,q} имеет в качестве двойственной мозаику {q,p} (симметричны диагонали таблицы). Самодвойственные мозаики {3,3}, {4,4}, {5,5}, и т.д. располагаются на диагонали таблицы.
| Сферические (Платоновы)/Евклидовы/гиперболические (диск Пуанкаре: компактные/паракомпактные/некомпактные) замощения с их символами Шлефли | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p \ q | 3 | 4 | 5 | 6 | 7 | 8 | ... | ∞ | ... | iπ/λ |
| 3 |  (тетраэдр) {3,3} |
 (октаэдр) {3,4} |
 (икосаэдр) {3,5} |
 (дельта-плитка) {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} |
 {3,iπ/λ} | ||
| 4 |  (куб) {4,3} |
 (кадриль) {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8} |
 {4,∞} |
{4,iπ/λ} | ||
| 5 |  (додекаэдр) {5,3} |
 {5,4} |
 {5,5} |
 {5,6} |
 {5,7} |
 {5,8} |
 {5,∞} |
{5,iπ/λ} | ||
| 6 |  (гексаплитка) {6,3} |
 {6,4} |
 {6,5} |
 {6,6} |
 {6,7} |
 {6,8} |
 {6,∞} |
{6,iπ/λ} | ||
| 7 |  {7,3} |
 {7,4} |
 {7,5} |
 {7,6} |
 {7,7} |
 {7,8} |
 {7,∞} |
{7,iπ/λ} | ||
| 8 |  {8,3} |
 {8,4} |
 {8,5} |
 {8,6} |
 {8,7} |
 {8,8} |
 {8,∞} |
{8,iπ/λ} | ||
| ... | ||||||||||
| ∞ |  {∞,3} |
 {∞,4} |
 {∞,5} |
 {∞,6} |
 {∞,7} |
 {∞,8} |
 {∞,∞} |
{∞,iπ/λ} | ||
| ... | ||||||||||
| iπ/λ |  {iπ/λ,3} |
{iπ/λ,4} |
{iπ/λ,5} |
{iπ/λ,6} |
{iπ/λ,7} |
{iπ/λ,8} |
{iπ/λ,∞} |
{iπ/λ,iπ/λ} | ||
(7 3 2)
Группа треугольника (7 3 2), группа Коксетера [7,3], орбифолд (*732) содержат эти однородные мозаики.
| Однородные семиугольные/треугольные мозаики | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [7,3], (*732) | [7,3]+, (732) | |||||||||
 |
 |
 |
 |
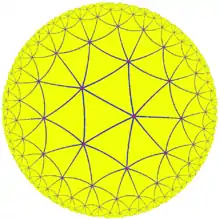 |
 |
 |
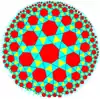 | |||
| {7,3} | t{7,3} | r{7,3} | 2t{7,3}=t{3,7} | 2r{7,3}={3,7} | rr{7,3} | tr{7,3} | sr{7,3} | |||
| Однородные двойственные мозаики | ||||||||||
 |
 |
 |
 |
 |
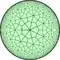 |
 |
 | |||
| V73 | V3.14.14 | V3.7.3.7 | V6.6.7 | V37 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | |||
(8 3 2)
Группа треугольника (8 3 2), группа Коксетера [8,3], орбифолд (*832) содержат эти однородные мозаики.
| Однородные восьмиугольные/треугольные мозаики | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [8,3], (*832) | [8,3]+ (832) |
[1+,8,3] (*443) |
[8,3+] (3*4) | ||||||||||
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} | rr{8,3} s2{3,8} |
tr{8,3} | sr{8,3} | h{8,3} | h2{8,3} | s{3,8} | |||
| Однородные двойственные | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V(3.4)3 | V8.6.6 | V35.4 | |||
(5 4 2)
Группа треугольника (5 4 2), группа Коксетера [5,4], орбифолд (*542) содержат эти однородные мозаики.
| Однородные пятиугольные/квадратные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [5,4], (*542) | [5,4]+, (542) | [5+,4], (5*2) | [5,4,1+], (*552) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| {5,4} | t{5,4} | r{5,4} | 2t{5,4}=t{4,5} | 2r{5,4}={4,5} | rr{5,4} | tr{5,4} | sr{5,4} | s{5,4} | h{4,5} | ||
| Однородные двойственные | |||||||||||
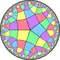
 |
 |
 |
 |
 |
 |
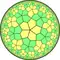
 |
 |
 | |||
| V54 | V4.10.10 | V4.5.4.5 | V5.8.8 | V45 | V4.4.5.4 | V4.8.10 | V3.3.4.3.5 | V3.3.5.3.5 | V55 | ||
(6 4 2)
Группа треугольника (6 4 2), группа Коксетера [6,4], орбифолд (*642) содержат эти однородные мозаики. Поскольку все элементы чётны, из двух двойственных однородных мозаик одна представляет фундаментальную область зеркальной симметрии: *3333, *662, *3232, *443, *222222, *3222 и *642 соответственно. Все семь мозаик могут быть альтернированы и для полученных мозаик существуют двойственные.
| Однородные четырёхшестиугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,4], (*642) ( [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (и [(∞,3,∞,3)] (*3232) подсимметрия) | |||||||||||
= = = |
= |
= = = |
= |
= = = |
= |
||||||
 |
 |
 |
 |
 |
 |
 | |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Однородные двойственные duals | |||||||||||
 |
 |
 |
 |
 |
 |
 | |||||
| V64 | V4.12.12 | V(4.6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Альтернирования | |||||||||||
| [1+,6,4] (*443) |
[6+,4] (6*2) |
[6,1+,4] (*3222) |
[6,4+] (4*3) |
[6,4,1+] (*662) |
[(6,4,2+)] (2*32) |
[6,4]+ (642) | |||||
= |
= |
= |
= |
= |
= |
||||||
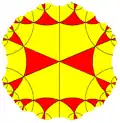
 |
 |
 |
 |
 |
 |
 | |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
(7 4 2)
Группа треугольника (7 4 2), группа Коксетера [7,4], орбифолд (*742) содержат эти однородные мозаики.
| Однородные семиугольные/квадратные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [7,4], (*742) | [7,4]+, (742) | [7+,4], (7*2) | [7,4,1+], (*772) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| {7,4} | t{7,4} | r{7,4} | 2t{7,4}=t{4,7} | 2r{7,4}={4,7} | rr{7,4} | tr{7,4} | sr{7,4} | s{7,4} | h{4,7} | ||
| Однородные двойственные | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| V74 | V4.14.14 | V4.7.4.7 | V7.8.8 | V47 | V4.4.7.4 | V4.8.14 | V3.3.4.3.7 | V3.3.7.3.7 | V77 | ||
(8 4 2)
Группа треугольника (8 4 2), группа Коксетера [8,4], орбифолд (*842) содержат эти однородные мозаики. Поскольку все элементы чётны, из двух двойственных однородных мозаик одна представляет фундаментальную область зеркальной симметрии: *4444, *882, *4242, *444, *22222222, *4222 и *842 соответственно. Все семь мозаик могут быть альтернированы и для полученных мозаик существуют двойственные.
| Однородные восьмиугольные/квадратные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (и подсимметрия [(∞,4,∞,4)] (*4242) ) | |||||||||||
= = = |
= |
= = = |
= |
= = |
= |
||||||
 |
 |
 |
 |
 |
 |
 | |||||
| {8,4} | t{8,4} |
r{8,4} | 2t{8,4}=t{4,8} | 2r{8,4}={4,8} | rr{8,4} | tr{8,4} | |||||
| Однордные двойственные | |||||||||||
 |
 |
 |
 |
 |
 |
 | |||||
| V84 | V4.16.16 | V(4.8)2 | V8.8.8 | V48 | V4.4.4.8 | V4.8.16 | |||||
| Альтернированные | |||||||||||
| [1+,8,4] (*444) |
[8+,4] (8*2) |
[8,1+,4] (*4222) |
[8,4+] (4*4) |
[8,4,1+] (*882) |
[(8,4,2+)] (2*42) |
[8,4]+ (842) | |||||
= |
= |
= |
= |
= |
= |
||||||
 |
 |
 |
 |
 |
 |
 | |||||
| h{8,4} | s{8,4} | hr{8,4} | s{4,8} | h{4,8} | hrr{8,4} | sr{8,4} | |||||
| Альтернированные двойственные | |||||||||||
 |
 |
 |
 |
 |
|||||||
| V(4.4)4 | V3.(3.8)2 | V(4.4.4)2 | V(3.4)3 | V88 | V4.44 | V3.3.4.3.8 | |||||
(5 5 2)
Группа треугольника (5 5 2), группа Коксетера [5,5], орбифолд (*552) содержат эти однородные мозаики.
| Однородные пятипятиугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [5,5], (*552) | [5,5]+, (552) | ||||||||||
= |
= |
= |
= |
= |
= |
= |
= | ||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| {5,5} | t{5,5} |
r{5,5} | 2t{5,5}=t{5,5} | 2r{5,5}={5,5} | rr{5,5} | tr{5,5} | sr{5,5} | ||||
| Однородные двойственные duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
|||||
| V5.5.5.5.5 | V5.10.10 | V5.5.5.5 | V5.10.10 | V5.5.5.5.5 | V4.5.4.5 | V4.10.10 | V3.3.5.3.5 | ||||
(6 5 2)
Группа треугольника (6 5 2), группа Коксетера [6,5], орбифолд (*652) содержат эти однородные мозаики.
| Однородные шестиугольные/пятиугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,5], (*652) | [6,5]+, (652) | [6,5+], (5*3) | [1+,6,5], (*553) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 | |||
| {6,5} | t{6,5} | r{6,5} | 2t{6,5}=t{5,6} | 2r{6,5}={5,6} | rr{6,5} | tr{6,5} | sr{6,5} | s{5,6} | h{6,5} | ||
| Однородные двойственные | |||||||||||
 |
 |
 |
 |
 |
 |
 |
|||||
| V65 | V5.12.12 | V5.6.5.6 | V6.10.10 | V56 | V4.5.4.6 | V4.10.12 | V3.3.5.3.6 | V3.3.3.5.3.5 | V(3.5)5 | ||
(6 6 2)
Группа треугольника (6 6 2), группа Коксетера [6,6], орбифолд (*662) содержат эти однородные мозаики.
| Однородные шестишестиугольные мозаики | ||||||
|---|---|---|---|---|---|---|
| Симметрия: [6,6], (*662) | ||||||
= |
= |
= |
= |
= |
= |
= |
 |
 |
 |
 |
 |
 |
 |
| {6,6} = h{4,6} |
t{6,6} = h2{4,6} |
r{6,6} {6,4} |
t{6,6} = h2{4,6} |
{6,6} = h{4,6} |
rr{6,6} r{6,4} |
tr{6,6} t{6,4} |
| Однородные двойственные | ||||||
 |
 |
 |
 |
 |
 |
 |
| V66 | V6.12.12 | V6.6.6.6 | V6.12.12 | V66 | V4.6.4.6 | V4.12.12 |
| Альтернированные | ||||||
| [1+,6,6] (*663) |
[6+,6] (6*3) |
[6,1+,6] (*3232) |
[6,6+] (6*3) |
[6,6,1+] (*663) |
[(6,6,2+)] (2*33) |
[6,6]+ (662) |
 |
 |
 |
 |
 | ||
| h{6,6} | s{6,6} | hr{6,6} | s{6,6} | h{6,6} | hrr{6,6} | sr{6,6} |
(8 6 2)
Группа треугольника (8 6 2), группа Коксетера [8,6], орбифолд (*862) содержат эти однородные мозаики.
| Однородные восьмиугольные/шестиугольные мозаики | ||||||
|---|---|---|---|---|---|---|
| Симметрия: [8,6], (*862) | ||||||
 |
 |
 |
 |
 |
 |
 |
| {8,6} | t{8,6} |
r{8,6} | 2t{8,6}=t{6,8} | 2r{8,6}={6,8} | rr{8,6} | tr{8,6} |
| Однородные двойственные | ||||||
 |
 |
 |
 |
 |
 |
 |
| V86 | V6.16.16 | V(6.8)2 | V8.12.12 | V68 | V4.6.4.8 | V4.12.16 |
| Альтернированные | ||||||
| [1+,8,6] (*466) |
[8+,6] (8*3) |
[8,1+,6] (*4232) |
[8,6+] (6*4) |
[8,6,1+] (*883) |
[(8,6,2+)] (2*43) |
[8,6]+ (862) |
 |
 |
 | ||||
| h{8,6} | s{8,6} | hr{8,6} | s{6,8} | h{6,8} | hrr{8,6} | sr{8,6} |
| Альтернированные двойственные | ||||||
 |
||||||
| V(4.6)6 | V3.3.8.3.8.3 | V(3.4.4.4)2 | V3.4.3.4.3.6 | V(3.8)8 | V3.45 | V3.3.6.3.8 |
(7 7 2)
Группа треугольника (7 7 2), группа Коксетера [7,7], орбифолд (*772) содержат эти однородные мозаики.
| Однородные семисемиугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [7,7], (*772) | [7,7]+, (772) | ||||||||||
= |
= |
= |
= |
= |
= |
= |
= | ||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| {7,7} | t{7,7} |
r{7,7} | 2t{7,7}=t{7,7} | 2r{7,7}={7,7} | rr{7,7} | tr{7,7} | sr{7,7} | ||||
| Однородные двойственные | |||||||||||
 |
 |
 |
 |
 |
 |
 |
|||||
| V77 | V7.14.14 | V7.7.7.7 | V7.14.14 | V77 | V4.7.4.7 | V4.14.14 | V3.3.7.3.7 | ||||
(8 8 2)
Группа треугольника (8 8 2), группа Коксетера [8,8], орбифолд (*882) содержат эти однородные мозаики.
| Однородные восьмивосьмиугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [8,8], (*882) | |||||||||||
= |
= |
= |
= |
= |
= |
= | |||||
 |
 |
 |
 |
 |
 |
 | |||||
| {8,8} | t{8,8} |
r{8,8} | 2t{8,8}=t{8,8} | 2r{8,8}={8,8} | rr{8,8} | tr{8,8} | |||||
| Однородные двойственные | |||||||||||
 |
 |
 |
 |
 |
 |
 | |||||
| V88 | V8.16.16 | V8.8.8.8 | V8.16.16 | V88 | V4.8.4.8 | V4.16.16 | |||||
| Альтернированные | |||||||||||
| [1+,8,8] (*884) |
[8+,8] (8*4) |
[8,1+,8] (*4242) |
[8,8+] (8*4) |
[8,8,1+] (*884) |
[(8,8,2+)] (2*44) |
[8,8]+ (882) | |||||
= |
= | ||||||||||
 |
 |
 |
 |
 | |||||||
| h{8,8} | s{8,8} | hr{8,8} | s{8,8} | h{8,8} | hrr{8,8} | sr{8,8} | |||||
| Альтернативные двойственные | |||||||||||
 |
 |
||||||||||
| V(4.8)8 | V3.4.3.8.3.8 | V(4.4)4 | V3.4.3.8.3.8 | V(4.8)8 | V46 | V3.3.8.3.8 | |||||
Фундаментальные треугольники общего вида
Существует бесконечно много семейств групп треугольников общего вида (p q r). В статье показаны однородные мозаики 9 семейств: (4 3 3), (4 4 3), (4 4 4), (5 3 3), (5 4 3), (5 4 4), (6 3 3), (6 4 3) и (6 4 4).
(4 3 3)
Группа треугольника (4 3 3), группа Коксетера [(4,3,3)], орбифолд (*433) содержат эти однородные мозаики. Без прямого угла в фундаментальном треугольнике построения Витхоффа слегка отличаются. Например, в семействе треугольников (4,3,3) плосконосая форма имеет шесть многоугольников вокруг вершины и её двойственная форма имеет шестиугольники, а не пятиугольники. В общем случае вершинная фигура плосконосой мозаики в треугольнике (p,q,r) имеет вид p.3.q.3.r.3, в частности, она имеет вид 4.3.3.3.3.3 для случая ниже.
| Однородные мозаики (4,3,3) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(4,3,3)], (*433) | [(4,3,3)]+, (433) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| h{8,3} t0(4,3,3) |
r{3,8}1/2 t0,1(4,3,3) |
h{8,3} t1(4,3,3) |
h2{8,3} t1,2(4,3,3) |
{3,8}1/2 t2(4,3,3) |
h2{8,3} t0,2(4,3,3) |
t{3,8}1/2 t0,1,2(4,3,3) |
s{3,8}1/2 s(4,3,3) | ||||
| Однородные двойственные | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| V(3.4)3 | V3.8.3.8 | V(3.4)3 | V3.6.4.6 | V(3.3)4 | V3.6.4.6 | V6.6.8 | V3.3.3.3.3.4 | ||||
(4 4 3)
Группа треугольника (4 4 3), группа Коксетера [(4,4,3)], орбифолд (*443) содержат эти однородные мозаики.
| Однородные мозаики (4,4,3) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(4,4,3)] (*443) | [(4,4,3)]+ (443) |
[(4,4,3+)] (3*22) |
[(4,1+,4,3)] (*3232) | |||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| h{6,4} t0(4,4,3) |
h2{6,4} t0,1(4,4,3) |
{4,6}1/2 t1(4,4,3) |
h2{6,4} t1,2(4,4,3) |
h{6,4} t2(4,4,3) |
r{6,4}1/2 t0,2(4,4,3) |
t{4,6}1/2 t0,1,2(4,4,3) |
s{4,6}1/2 s(4,4,3) |
hr{4,6}1/2 hr(4,3,4) |
h{4,6}1/2 h(4,3,4) |
q{4,6} h1(4,3,4) |
| Однородные двойственные | ||||||||||
 |
 |
 |
 |
|||||||
| V(3.4)4 | V3.8.4.8 | V(4.4)3 | V3.8.4.8 | V(3.4)4 | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V(4.4.3)2 | V66 | V4.3.4.6.6 |
(4 4 4)
Группа треугольника (4 4 4), группа Коксетера [(4,4,4)], орбифолд (*444) содержат эти однородные мозаики.
| Однородные мозаики (4,4,4) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(4,4,4)], (*444) | [(4,4,4)]+ (444) |
[(1+,4,4,4)] (*4242) |
[(4+,4,4)] (4*22) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| t0(4,4,4) h{8,4} |
t0,1(4,4,4) h2{8,4} |
t1(4,4,4) {4,8}1/2 |
t1,2(4,4,4) h2{8,4} |
t2(4,4,4) h{8,4} |
t0,2(4,4,4) r{4,8}1/2 |
t0,1,2(4,4,4) t{4,8}1/2 |
s(4,4,4) s{4,8}1/2 |
h(4,4,4) h{4,8}1/2 |
hr(4,4,4) hr{4,8}1/2 | ||
| Однородные двойственные | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V8.8.8 | V3.4.3.4.3.4 | V88 | V(4,4)3 | ||
(5 3 3)
Группа треугольника (5 3 3), группа Коксетера [(5,3,3)], орбифолд (*533) содержат эти однородные мозаики.
| Однородные мозаики (5,3,3) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(5,3,3)], (*533) | [(5,3,3)]+, (533) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| h{10,3} t0(5,3,3) |
r{3,10}1/2 t0,1(5,3,3) |
h{10,3} t1(5,3,3) |
h2{10,3} t1,2(5,3,3) |
{3,10}1/2 (5,3,3) |
h2{10,3} t0,2(5,3,3) |
t{3,10}1/2 t0,1,2(5,3,3) |
s{3,10}1/2 ht0,1,2(5,3,3) | ||||
| Однородные двойственные | |||||||||||
 |
 |
||||||||||
| V(3.5)3 | V3.10.3.10 | V(3.5)3 | V3.6.5.6 | V(3.3)5 | V3.6.5.6 | V6.6.10 | V3.3.3.3.3.5 | ||||
(5 4 3)
Группа треугольника (5 4 3), группа Коксетера [(5,4,3)], орбифолд (*543) содержат эти однородные мозаики.
| Однородные мозаики (5,4,3) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(5,4,3)], (*543) | [(5,4,3)]+, (543) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| t0(5,4,3) (5,4,3) |
t0,1(5,4,3) r(3,5,4) |
t1(5,4,3) (4,3,5) |
t1,2(5,4,3) r(5,4,3) |
t2(5,4,3) (3,5,4) |
t0,2(5,4,3) r(4,3,5) |
t0,1,2(5,4,3) t(5,4,3) |
s(5,4,3) | ||||
| Однородные двойственные | |||||||||||
 |
|||||||||||
| V(3.5)4 | V3.10.4.10 | V(4.5)3 | V3.8.5.8 | V(3.4)5 | V4.6.5.6 | V6.8.10 | V3.5.3.4.3.3 | ||||
(5 4 4)
Группа треугольника (5 4 4), группа Коксетера [(5,4,4)], орбифолд (*544) содержат эти однородные мозаики.
| Однородные мозаики (5,4,4) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(5,4,4)] (*544) |
[(5,4,4)]+ (544) |
[(5+,4,4)] (5*22) |
[(5,4,1+,4)] (*5222) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
||||
| t0(5,4,4) h{10,4} |
t0,1(5,4,4) r{4,10}1/2 |
t1(5,4,4) h{10,4} |
t1,2(5,4,4) h2{10,4} |
t2(5,4,4) {4,10}1/2 |
t0,2(5,4,4) h2{10,4} |
t0,1,2(5,4,4) t{4,10}1/2 |
s(4,5,4) s{4,10}1/2 |
h(4,5,4) h{4,10}1/2 |
hr(4,5,4) hr{4,10}1/2 | ||
| Однородные двойственные | |||||||||||
 |
 |
 |
|||||||||
| V(4.5)4 | V4.10.4.10 | V(4.5)4 | V4.8.5.8 | V(4.4)5 | V4.8.5.8 | V8.8.10 | V3.4.3.4.3.5 | V1010 | V(4.4.5)2 | ||
(6 3 3)
Группа треугольника (6 3 3), группа Коксетера [(6,3,3)], орбифолд (*633) содержат эти однородные мозаики.
| Однородные мозаики (6,3,3) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(6,3,3)], (*633) | [(6,3,3)]+, (633) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| t0{(6,3,3)} h{12,3} |
t0,1{(6,3,3)} r{3,12}1/2 |
t1{(6,3,3)} h{12,3} |
t1,2{(6,3,3)} h2{12,3} |
t2{(6,3,3)} {3,12}1/2 |
t0,2{(6,3,3)} h2{12,3} |
t0,1,2{(6,3,3)} t{3,12}1/2 |
s{(6,3,3)} s{3,12}1/2 | ||||
| Однородные двойственные | |||||||||||
 |
 |
||||||||||
| V(3.6)3 | V3.12.3.12 | V(3.6)3 | V3.6.6.6 | V(3.3)6 {12,3} |
V3.6.6.6 | V6.6.12 | V3.3.3.3.3.6 | ||||
(6 4 3)
Группа треугольника (6 4 3), группа Коксетера [(6,4,3)], орбифолд (*643) содержат эти однородные мозаики.
| Однородные мозаики (6,4,3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(6,4,3)] (*643) |
[(6,4,3)]+ (643) |
[(6,1+,4,3)] (*3332) |
[(6,4,3+)] (3*32) | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
||
| t0{(6,4,3)} | t0,1{(6,4,3)} | t1{(6,4,3)} | t1,2{(6,4,3)} | t2{(6,4,3)} | t0,2{(6,4,3)} | t0,1,2{(6,4,3)} | s{(6,4,3)} | h{(6,4,3)} | hr{(6,4,3)} |
| Однородные двойственные | |||||||||
 |
 |
 |
|||||||
| V(3.6)4 | V3.12.4.12 | V(4.6)3 | V3.8.6.8 | V(3.4)6 | V4.6.6.6 | V6.8.12 | V3.6.3.4.3.3 | V(3.6.6)3 | V4.(3.4)3 |
(6 4 4)
Группа треугольника (6 4 4), группа Коксетера [(6,4,4)], орбифолд (*644) содержат эти однородные мозаики.
| Однородные мозаики 6-4-4 | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [(6,4,4)], (*644) | (644) | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
| (6,4,4) h{12,4} |
t0,1(6,4,4) r{4,12}1/2 |
t1(6,4,4) h{12,4} |
t1,2(6,4,4) h2{12,4} |
t2(6,4,4) {4,12}1/2 |
t0,2(6,4,4) h2{12,4} |
t0,1,2(6,4,4) t{4,12}1/2 |
s(6,4,4) s{4,12}1/2 |
| Однородные двойственные | |||||||
 |
 |
 |
 |
 |
 |
 |
|
| V(4.6)4 | V(4.12)2 | V(4.6)4 | V4.8.6.8 | V412 | V4.8.6.8 | V8.8.12 | V4.6.4.6.6.6 |
Сводная таблица мозаик с конечной треугольной конечной областью
Таблица всех однородных гиперболических мозаик с Фундаментальной областью (p q r), where 2 ≤ p,q,r ≤ 8.
- См. Шаблон:Таблица конечных треугольных гиперболических мозаик
Четырёхугольные фундаментальные области
(3 2 2 2)
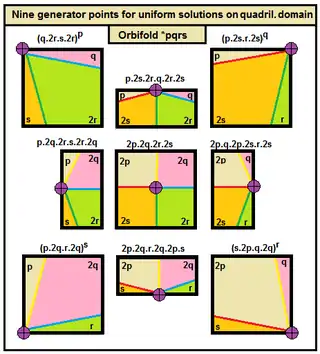
Четырёхугольные фундаментальные области также существуют на гиперболической плоскости с орбифолдом *3222 ([∞,3,∞] в нотации Коксетера) как наименьшее семейство. Существует 9 положений генератора для получения однородной мозаики внутри четырёхугольной фундаментальной области. Вершинная фигура может быть выделена из фундаментальной области как 3 случая (1) Угол (2) Середина ребра и (3) Центр. Если генерирующая точка смежна углам опрядка 2, в этом углу образуется вырожденная грань {2} в виде двуугольника, но её можно отбросить. Плосконосые и альтернированные однородные мозаики могут также быть получены (не показаны), если вершинная фигура содержит только грани с чётным числом сторон.
Диаграммы Коксетера — Дынкина четырёхугольных фундаментальных областей рассматриваются как вырожденный граф тетраэдра с 2 из 6 рёбер, помеченных бесконечностью или пунктирными линиями. Логическое требование, чтобы по меньшей мере одно из двух параллельных зеркал было активным, ограничивает число возможных вариантов до 9 и другие помеченные кружками варианты неприменимы.
| Однородные мозаики с симметрией *3222 | ||||
|---|---|---|---|---|
 |
.png.webp) |
 |
 | |
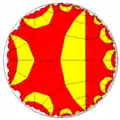 |
 |
.png.webp) | ||
 |
 |
 | ||
(3 2 3 2)
| Подобные H2 мозаики с симметрией *3232 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Диаграммы Коксетера |
||||||||
| Вершинная фигура |
66 | (3.4.3.4)2 | 3.4.6.6.4 | 6.4.6.4 | ||||
| Мозаика | 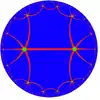 |
 |
 |
 | ||||
| Двойственная | 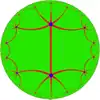 |
 | ||||||
Воображаемые треугольные фундаментальные области
Существует бесконечно много семейств групп треугольника, включающие бесконечные порядки. В статье приведены однородные мозаики 9 семейств: (∞ 3 2), (∞ 4 2), (∞ ∞ 2), (∞ 3 3), (∞ 4 3), (∞ 4 4), (∞ ∞ 3), (∞ ∞ 4) и (∞ ∞ ∞).
(∞ 3 2)
Воображаемая (∞ 3 2) группа треугольника, группа Коксетера [∞,3], орбифолд (*∞32) содержат эти однородные мозаики.
| Паракомпактные однородные мозаики в семействе [∞,3] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [∞,3], (*∞32) | [∞,3]+ (∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) | |||||||
= |
= |
= |
= | |||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | h2{∞,3} | s{3,∞} |
| Однородные двойственные | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
||
| V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
(∞ 4 2)
Воображаемая (∞ 42) группа треугольника, группа Коксетера [∞,4], орбифолд (*∞42) содержат эти однородные мозаики.
| Паракомпактные однородные мозаики в семействе [∞,4] | |||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 | |
| {∞,4} | t{∞,4} | r{∞,4} | 2t{∞,4}=t{4,∞} | 2r{∞,4}={4,∞} | rr{∞,4} | tr{∞,4} | |
| Двойственные фигуры | |||||||
 |
 |
 |
 |
 |
 |
 | |
| V∞4 | V4.∞.∞ | V(4.∞)2 | V8.8.∞ | V4∞ | V43.∞ | V4.8.∞ | |
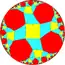
| Альтернированные | |||||||
| [1+,∞,4] (*44∞) |
[∞+,4] (∞*2) |
[∞,1+,4] (*2∞2∞) |
[∞,4+] (4*∞) |
[∞,4,1+] (*∞∞2) |
[(∞,4,2+)] (2*2∞) |
[∞,4]+ (∞42) | |
= |
= |
||||||
| h{∞,4} | s{∞,4} | hr{∞,4} | s{4,∞} | h{4,∞} | hrr{∞,4} | s{∞,4} | |
 |
 |
 |
 | ||||
| Alternation duals | |||||||
 |
 |
||||||
| V(∞.4)4 | V3.(3.∞)2 | V(4.∞.4)2 | V3.∞.(3.4)2 | V∞∞ | V∞.44 | V3.3.4.3.∞ | |
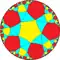
(∞ 5 2)
Воображаемая (∞ 5 2) группа треугольника, группа Коксетера [∞,5], орбифолд (*∞52) содержат эти однородные мозаики.
| Паракомпактные однородные бесконечноугольные/пятиугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [∞,5], (*∞52) | [∞,5]+ (∞52) |
[1+,∞,5] (*∞55) |
[∞,5+] (5*∞) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||
| {∞,5} | t{∞,5} | r{∞,5} | 2t{∞,5}=t{5,∞} | 2r{∞,5}={5,∞} | rr{∞,5} | tr{∞,5} | sr{∞,5} | h{∞,5} | h2{∞,5} | s{5,∞} | |
| Uniform duals | |||||||||||
 |
 |
 |
 |
||||||||
| V∞5 | V5.∞.∞ | V5.∞.5.∞ | V∞.10.10 | V5∞ | V4.5.4.∞ | V4.10.∞ | V3.3.5.3.∞ | V(∞.5)5 | V3.5.3.5.3.∞ | ||
(∞ ∞ 2)
Воображаемая (∞ ∞ 2) группа треугольника, группа Коксетера [∞,∞],орбифолд (*∞∞2) содержат эти однородные мозаики.
| Паракомпактные однородные мозаики семейства [∞,∞] | ||||||
|---|---|---|---|---|---|---|
= = |
= = |
= = |
= = |
= = |
= |
= |
 |
 |
 |
 |
 |
 |
 |
| {∞,∞} | t{∞,∞} | r{∞,∞} | 2t{∞,∞}=t{∞,∞} | 2r{∞,∞}={∞,∞} | rr{∞,∞} | tr{∞,∞} |
| Двойственные мозаики | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞ | V(∞.∞)2 | V∞.∞.∞ | V∞∞ | V4.∞.4.∞ | V4.4.∞ |
| Альтернированные | ||||||
| [1+,∞,∞] (*∞∞2) |
[∞+,∞] (∞*∞) |
[∞,1+,∞] (*∞∞∞∞) |
[∞,∞+] (∞*∞) |
[∞,∞,1+] (*∞∞2) |
[(∞,∞,2+)] (2*∞∞) |
[∞,∞]+ (2∞∞) |
 |
 |
 |
 |
 |
 | |
| h{∞,∞} | s{∞,∞} | hr{∞,∞} | s{∞,∞} | h2{∞,∞} | hrr{∞,∞} | sr{∞,∞} |
| Альтернированные двойственные | ||||||
 |
 |
 |
 | |||
| V(∞.∞)∞ | V(3.∞)3 | V(∞.4)4 | V(3.∞)3 | V∞∞ | V(4.∞.4)2 | V3.3.∞.3.∞ |
(∞ 3 3)
Воображаемая (∞ 3 3) группа треугольника, группа Коксетера [(∞,3,3)], орбифолд (*∞33) содержат эти однородные мозаики.
| Паракомпактные гиперболические однородные мозаики семейства [(∞,3,3)] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(∞,3,3)], (*∞33) | [(∞,3,3)]+, (∞33) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| (∞,∞,3) | t0,1(∞,3,3) | t1(∞,3,3) | t1,2(∞,3,3) | t2(∞,3,3) | t0,2(∞,3,3) | t0,1,2(∞,3,3) | s(∞,3,3) | ||||
| Двойственные мозаики | |||||||||||
 |
 |
||||||||||
| V(3.∞)3 | V3.∞.3.∞ | V(3.∞)3 | V3.6.∞.6 | V(3.3)∞ | V3.6.∞.6 | V6.6.∞ | V3.3.3.3.3.∞ | ||||
(∞ 4 3)
Воображаемая (∞ 4 3) группа треугольника, группа Коксетера [(∞,4,3)], орбифолд (*∞43) содержат эти однородные мозаики.
| Паракомпактные гиперболические однородные мозаики семейства [(∞,4,3)] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(∞,4,3)] (*∞43) |
[(∞,4,3)]+ (∞43) |
[(∞,4,3+)] (3*4∞) |
[(∞,1+,4,3)] (*∞323) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
||||
| (∞,4,3) | t0,1(∞,4,3) | t1(∞,4,3) | t1,2(∞,4,3) | t2(∞,4,3) | t0,2(∞,4,3) | t0,1,2(∞,4,3) | s(∞,4,3) | ht0,2(∞,4,3) | ht1(∞,4,3) | ||
| Двойственные мозаики | |||||||||||
 |
 |
 |
|||||||||
| V(3.∞)4 | V3.∞.4.∞ | V(4.∞)3 | V3.8.∞.8 | V(3.4)∞ | 4.6.∞.6 | V6.8.∞ | V3.3.3.4.3.∞ | V(4.3.4)2.∞ | V(6.∞.6)3 | ||
(∞ 4 4)
Воображаемая (∞ 4 4) группа треугольника, группа Коксетера [(∞,4,4)], орбифолд (*∞44) содержат эти однородные мозаики.
| Паракомпактные гиперболические однородные мозаики семейства [(4,4,∞)] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(4,4,∞)], (*44∞) | (44∞) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| (4,4,∞) h{∞,4} |
t0,1(4,4,∞) r{4,∞}1/2 |
t1(4,4,∞) h{4,∞}1/2 |
t1,2(4,4,∞) h2{∞,4} |
t2(4,4,∞) {4,∞}1/2 |
t0,2(4,4,∞) h2{∞,4} |
t0,1,2(4,4,∞) t{4,∞}1/2 |
s(4,4,∞) s{4,∞}1/2 | ||||
| Двойственные мозаики | |||||||||||
 |
 |
 |
 |
 |
 |
 |
|||||
| V(4.∞)4 | V4.∞.4.∞ | V(4.∞)4 | V4.∞.4.∞ | V4∞ | V4.∞.4.∞ | V8.8.∞ | V3.4.3.4.3.∞ | ||||
(∞ ∞ 3)
Воображаемая (∞ ∞ 3) группа треугольника, группа Коксетера [(∞,∞,3)], орбифолд (*∞∞3) содержат эти однородные мозаики.
| Паракомпактные гиперболические однородные мозаики семейства [(∞,∞,3)] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(∞,∞,3)], (*∞∞3) | [(∞,∞,3)]+ (∞∞3) |
[(∞,∞,3+)] (3*∞∞) |
[(∞,1+,∞,3)] (*∞3∞3) | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| (∞,∞,3) h{6,∞} |
t0,1(∞,∞,3) h2{6,∞} |
t1(∞,∞,3) {∞,6}1/2 |
t1,2(∞,∞,3) h2{6,∞} |
t2(∞,∞,3) h{6,∞} |
t0,2(∞,∞,3) r{∞,6}1/2 |
t0,1,2(∞,∞,3) t{∞,6}1/2 |
s(∞,∞,3) s{∞,6}1/2 |
hr0,2(∞,∞,3) hr{∞,6}1/2 |
hr1(∞,∞,3) h{∞,6}1/2 |
| Двойственные мозаики | |||||||||
 |
 |
 |
 | ||||||
| V(3.∞)∞ | V3.∞.∞.∞ | V(∞.∞)3 | V3.∞.∞.∞ | V(3.∞)∞ | V(6.∞)2 | V6.∞.∞ | V3.∞.3.∞.3.3 | V(3.4.∞.4)2 | V(∞.6)6 |
(∞ ∞ 4)
Воображаемая (∞ ∞ 4) группа треугольника, группа Коксетера [(∞,∞,4)], орбифолд (*∞∞4) содержат эти однородные мозаики.
| Паракомпактные гиперболические однородные мозаики семейства [(∞,∞,4)] | ||||||
|---|---|---|---|---|---|---|
| Symmetry: [(∞,∞,4)], (*∞∞4) | ||||||
 |
 |
 |
 |
 |
 |
 |
| (∞,∞,4) h{8,∞} |
t0,1(∞,∞,4) h2{8,∞} |
t1(∞,∞,4) {∞,8} |
t1,2(∞,∞,4) h2{∞,8} |
t2(∞,∞,4) h{8,∞} |
t0,2(∞,∞,4) r{∞,8} |
t0,1,2(∞,∞,4) t{∞,8} |
| Двойственные мозаики | ||||||
 |
 |
 |
 |
 |
 |
 |
| V(4.∞)∞ | V∞.∞.∞.4 | V∞4 | V∞.∞.∞.4 | V(4.∞)∞ | V∞.∞.∞.4 | V∞.∞.8 |
| Альтернированные | ||||||
| [(1+,∞,∞,4)] (*2∞∞∞) |
[(∞+,∞,4)] (∞*2∞) |
[(∞,1+,∞,4)] (*2∞∞∞) |
[(∞,∞+,4)] (∞*2∞) |
[(∞,∞,1+,4)] (*2∞∞∞) |
[(∞,∞,4+)] (2*∞∞) |
[(∞,∞,4)]+ (4∞∞) |
 |
 |
 |
 | |||
| Альтернированные двойственные | ||||||
 |
 |
 |
||||
| V∞∞ | V∞.44 | V(∞.4)4 | V∞.44 | V∞∞ | V∞.44 | V3.∞.3.∞.3.4 |
(∞ ∞ ∞)
Воображаемая (∞ ∞ ∞) группа треугольника, группа Коксетера [(∞,∞,∞)], орбифолд (*∞∞∞) содержат эти однородные мозаики.
| Паракомпактные однородные мозаики семейства [(∞,∞,∞)] | ||||||
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
| (∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) r{∞,∞} |
t(∞,∞,∞) t{∞,∞} |
| Двойственные мозаики | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞.∞.∞ |
| Альтернированные | ||||||
| [(1+,∞,∞,∞)] (*∞∞∞∞) |
[∞+,∞,∞)] (∞*∞) |
[∞,1+,∞,∞)] (*∞∞∞∞) |
[∞,∞+,∞)] (∞*∞) |
[(∞,∞,∞,1+)] (*∞∞∞∞) |
[(∞,∞,∞+)] (∞*∞) |
[∞,∞,∞)]+ (∞∞∞) |
 |
 |
 |
 |
 |
 |
 |
| Альтернированные двойственные | ||||||
 |
 |
 |
 |
 |
 |
|
| V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V3.∞.3.∞.3.∞ |
Сводная таблица мозаик с бесконечными треугольными фундаментальными областями
Таблица всех однородных гиперболических мозаик с фундаментальной областью (p q r), где 2 ≤ p,q,r ≤ 8, и одно или более значений равно ∞.
| Бесконечные треугольные гиперболические мозаики | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (p q r) | t0 | h0 | t01 | h01 | t1 | h1 | t12 | h12 | t2 | h2 | t02 | h02 | t012 | s | |||||
 (∞ 3 2) |
t0{∞,3} ∞3 | h0{∞,3} (3.∞)3 | t01{∞,3} ∞.3.∞ | t1{∞,3} (3.∞)2 | t12{∞,3} 6.∞.6 | h12{∞,3} 3.3.3.∞.3.3 | t2{∞,3} 3∞ | t02{∞,3} 3.4.∞.4 | t012{∞,3} 4.6.∞ | s{∞,3} 3.3.3.3.∞ | |||||||||
 (∞ 4 2) |
t0{∞,4} ∞4 | h0{∞,4} (4.∞)4 | t01{∞,4} ∞.4.∞ | h01{∞,4} 3.∞.3.3.∞ | t1{∞,4} (4.∞)2 | h1{∞,4} (4.4.∞)2 | t12{∞,4} 8.∞.8 | h12{∞,4} 3.4.3.∞.3.4 | t2{∞,4} 4∞ | h2{∞,4} ∞∞ | t02{∞,4} 4.4.∞.4 | h02{∞,4} 4.4.4.∞.4 | t012{∞,4} 4.8.∞ | s{∞,4} 3.3.4.3.∞ | |||||
 (∞ 5 2) |
t0{∞,5} ∞5 | h0{∞,5} (5.∞)5 | t01{∞,5} ∞.5.∞ | t1{∞,5} (5.∞)2 | t12{∞,5} 10.∞.10 | h12{∞,5} 3.5.3.∞.3.5 | t2{∞,5} 5∞ | t02{∞,5} 5.4.∞.4 | t012{∞,5} 4.10.∞ | s{∞,5} 3.3.5.3.∞ | |||||||||
 (∞ 6 2) |
t0{∞,6} ∞6 | h0{∞,6} (6.∞)6 | t01{∞,6} ∞.6.∞ | h01{∞,6} 3.∞.3.3.3.∞ | t1{∞,6} (6.∞)2 | h1{∞,6} (4.3.4.∞)2 | t12{∞,6} 12.∞.12 | h12{∞,6} 3.6.3.∞.3.6 | t2{∞,6} 6∞ | h2{∞,6} (∞.3)∞ | t02{∞,6} 6.4.∞.4 | h02{∞,6} 4.3.4.4.∞.4 | t012{∞,6} 4.12.∞ | s{∞,6} 3.3.6.3.∞ | |||||
 (∞ 7 2) |
t0{∞,7} ∞7 | h0{∞,7} (7.∞)7 | t01{∞,7} ∞.7.∞ | t1{∞,7} (7.∞)2 | t12{∞,7} 14.∞.14 | h12{∞,7} 3.7.3.∞.3.7 | t2{∞,7} 7∞ | t02{∞,7} 7.4.∞.4 | t012{∞,7} 4.14.∞ | s{∞,7} 3.3.7.3.∞ | |||||||||
 (∞ 8 2) |
t0{∞,8} ∞8 | h0{∞,8} (8.∞)8 | t01{∞,8} ∞.8.∞ | h01{∞,8} 3.∞.3.4.3.∞ | t1{∞,8} (8.∞)2 | h1{∞,8} (4.4.4.∞)2 | t12{∞,8} 16.∞.16 | h12{∞,8} 3.8.3.∞.3.8 | t2{∞,8} 8∞ | h2{∞,8} (∞.4)∞ | t02{∞,8} 8.4.∞.4 | h02{∞,8} 4.4.4.4.∞.4 | t012{∞,8} 4.16.∞ | s{∞,8} 3.3.8.3.∞ | |||||
 (∞ ∞ 2) |
t0{∞,∞} ∞∞ | h0{∞,∞} (∞.∞)∞ | t01{∞,∞} ∞.∞.∞ | h01{∞,∞} 3.∞.3.∞.3.∞ | t1{∞,∞} ∞4 | h1{∞,∞} (4.∞)4 | t12{∞,∞} ∞.∞.∞ | h12{∞,∞} 3.∞.3.∞.3.∞ | t2{∞,∞} ∞∞ | h2{∞,∞} (∞.∞)∞ | t02{∞,∞} (∞.4)2 | h02{∞,∞} (4.∞.4)2 | t012{∞,∞} 4.∞.∞ | s{∞,∞} 3.3.∞.3.∞ | |||||
 (∞ 3 3) |
t0(∞,3,3) (∞.3)3 | t01(∞,3,3) (3.∞)2 | t1(∞,3,3) (3.∞)3 | t12(∞,3,3) 3.6.∞.6 | t2(∞,3,3) 3∞ | t02(∞,3,3) 3.6.∞.6 | t012(∞,3,3) 6.6.∞ | s(∞,3,3) 3.3.3.3.3.∞ | |||||||||||
 (∞ 4 3) |
t0(∞,4,3) (∞.3)4 | t01(∞,4,3) 3.∞.4.∞ | t1(∞,4,3) (4.∞)3 | h1(∞,4,3) (6.6.∞)3 | t12(∞,4,3) 3.8.∞.8 | t2(∞,4,3) (4.3)∞ | t02(∞,4,3) 4.6.∞.6 | h02(∞,4,3) 4.4.3.4.∞.4.3 | t012(∞,4,3) 6.8.∞ | s(∞,4,3) 3.3.3.4.3.∞ | |||||||||
 (∞ 5 3) |
t0(∞,5,3) (∞.3)5 | t01(∞,5,3) 3.∞.5.∞ | t1(∞,5,3) (5.∞)3 | t12(∞,5,3) 3.10.∞.10 | t2(∞,5,3) (5.3)∞ | t02(∞,5,3) 5.6.∞.6 | t012(∞,5,3) 6.10.∞ | s(∞,5,3) 3.3.3.5.3.∞ | |||||||||||
 (∞ 6 3) |
t0(∞,6,3) (∞.3)6 | t01(∞,6,3) 3.∞.6.∞ | t1(∞,6,3) (6.∞)3 | h1(∞,6,3) (6.3.6.∞)3 | t12(∞,6,3) 3.12.∞.12 | t2(∞,6,3) (6.3)∞ | t02(∞,6,3) 6.6.∞.6 | h02(∞,6,3) 4.3.4.3.4.∞.4.3 | t012(∞,6,3) 6.12.∞ | s(∞,6,3) 3.3.3.6.3.∞ | |||||||||
 (∞ 7 3) |
t0(∞,7,3) (∞.3)7 | t01(∞,7,3) 3.∞.7.∞ | t1(∞,7,3) (7.∞)3 | t12(∞,7,3) 3.14.∞.14 | t2(∞,7,3) (7.3)∞ | t02(∞,7,3) 7.6.∞.6 | t012(∞,7,3) 6.14.∞ | s(∞,7,3) 3.3.3.7.3.∞ | |||||||||||
 (∞ 8 3) |
t0(∞,8,3) (∞.3)8 | t01(∞,8,3) 3.∞.8.∞ | t1(∞,8,3) (8.∞)3 | h1(∞,8,3) (6.4.6.∞)3 | t12(∞,8,3) 3.16.∞.16 | t2(∞,8,3) (8.3)∞ | t02(∞,8,3) 8.6.∞.6 | h02(∞,8,3) 4.4.4.3.4.∞.4.3 | t012(∞,8,3) 6.16.∞ | s(∞,8,3) 3.3.3.8.3.∞ | |||||||||
 (∞ ∞ 3) |
t0(∞,∞,3) (∞.3)∞ | t01(∞,∞,3) 3.∞.∞.∞ | t1(∞,∞,3) ∞6 | h1(∞,∞,3) (6.∞)6 | t12(∞,∞,3) 3.∞.∞.∞ | t2(∞,∞,3) (∞.3)∞ | t02(∞,∞,3) (∞.6)2 | h02(∞,∞,3) (4.∞.4.3)2 | t012(∞,∞,3) 6.∞.∞ | s(∞,∞,3) 3.3.3.∞.3.∞ | |||||||||
 (∞ 4 4) |
t0(∞,4,4) (∞.4)4 | h0(∞,4,4) (8.∞.8)4 | t01(∞,4,4) (4.∞)2 | h01(∞,4,4) (4.4.∞)2 | t1(∞,4,4) (4.∞)4 | h1(∞,4,4) (8.8.∞)4 | t12(∞,4,4) 4.8.∞.8 | h12(∞,4,4) 4.4.4.4.∞.4.4 | t2(∞,4,4) 4∞ | h2(∞,4,4) ∞∞ | t02(∞,4,4) 4.8.∞.8 | h02(∞,4,4) 4.4.4.4.∞.4.4 | t012(∞,4,4) 8.8.∞ | s(∞,4,4) 3.4.3.4.3.∞ | |||||
 (∞ 5 4) |
t0(∞,5,4) (∞.4)5 | h0(∞,5,4) (10.∞.10)5 | t01(∞,5,4) 4.∞.5.∞ | t1(∞,5,4) (5.∞)4 | t12(∞,5,4) 4.10.∞.10 | h12(∞,5,4) 4.4.5.4.∞.4.5 | t2(∞,5,4) (5.4)∞ | t02(∞,5,4) 5.8.∞.8 | t012(∞,5,4) 8.10.∞ | s(∞,5,4) 3.4.3.5.3.∞ | |||||||||
 (∞ 6 4) |
t0(∞,6,4) (∞.4)6 | h0(∞,6,4) (12.∞.12)6 | t01(∞,6,4) 4.∞.6.∞ | h01(∞,6,4) 4.4.∞.4.3.4.∞ | t1(∞,6,4) (6.∞)4 | h1(∞,6,4) (8.3.8.∞)4 | t12(∞,6,4) 4.12.∞.12 | h12(∞,6,4) 4.4.6.4.∞.4.6 | t2(∞,6,4) (6.4)∞ | h2(∞,6,4) (∞.3.∞)∞ | t02(∞,6,4) 6.8.∞.8 | h02(∞,6,4) 4.3.4.4.4.∞.4.4 | t012(∞,6,4) 8.12.∞ | s(∞,6,4) 3.4.3.6.3.∞ | |||||
 (∞ 7 4) |
t0(∞,7,4) (∞.4)7 | h0(∞,7,4) (14.∞.14)7 | t01(∞,7,4) 4.∞.7.∞ | t1(∞,7,4) (7.∞)4 | t12(∞,7,4) 4.14.∞.14 | h12(∞,7,4) 4.4.7.4.∞.4.7 | t2(∞,7,4) (7.4)∞ | t02(∞,7,4) 7.8.∞.8 | t012(∞,7,4) 8.14.∞ | s(∞,7,4) 3.4.3.7.3.∞ | |||||||||
 (∞ 8 4) |
t0(∞,8,4) (∞.4)8 | h0(∞,8,4) (16.∞.16)8 | t01(∞,8,4) 4.∞.8.∞ | h01(∞,8,4) 4.4.∞.4.4.4.∞ | t1(∞,8,4) (8.∞)4 | h1(∞,8,4) (8.4.8.∞)4 | t12(∞,8,4) 4.16.∞.16 | h12(∞,8,4) 4.4.8.4.∞.4.8 | t2(∞,8,4) (8.4)∞ | h2(∞,8,4) (∞.4.∞)∞ | t02(∞,8,4) 8.8.∞.8 | h02(∞,8,4) 4.4.4.4.4.∞.4.4 | t012(∞,8,4) 8.16.∞ | s(∞,8,4) 3.4.3.8.3.∞ | |||||
 (∞ ∞ 4) |
t0(∞,∞,4) (∞.4)∞ | h0(∞,∞,4) (∞.∞.∞)∞ | t01(∞,∞,4) 4.∞.∞.∞ | h01(∞,∞,4) 4.4.∞.4.∞.4.∞ | t1(∞,∞,4) ∞8 | h1(∞,∞,4) (8.∞)8 | t12(∞,∞,4) 4.∞.∞.∞ | h12(∞,∞,4) 4.4.∞.4.∞.4.∞ | t2(∞,∞,4) (∞.4)∞ | h2(∞,∞,4) (∞.∞.∞)∞ | t02(∞,∞,4) (∞.8)2 | h02(∞,∞,4) (4.∞.4.4)2 | t012(∞,∞,4) 8.∞.∞ | s(∞,∞,4) 3.4.3.∞.3.∞ | |||||
 (∞ 5 5) |
t0(∞,5,5) (∞.5)5 | t01(∞,5,5) (5.∞)2 | t1(∞,5,5) (5.∞)5 | t12(∞,5,5) 5.10.∞.10 | t2(∞,5,5) 5∞ | t02(∞,5,5) 5.10.∞.10 | t012(∞,5,5) 10.10.∞ | s(∞,5,5) 3.5.3.5.3.∞ | |||||||||||
 (∞ 6 5) |
t0(∞,6,5) (∞.5)6 | t01(∞,6,5) 5.∞.6.∞ | t1(∞,6,5) (6.∞)5 | h1(∞,6,5) (10.3.10.∞)5 | t12(∞,6,5) 5.12.∞.12 | t2(∞,6,5) (6.5)∞ | t02(∞,6,5) 6.10.∞.10 | h02(∞,6,5) 4.3.4.5.4.∞.4.5 | t012(∞,6,5) 10.12.∞ | s(∞,6,5) 3.5.3.6.3.∞ | |||||||||
 (∞ 7 5) |
t0(∞,7,5) (∞.5)7 | t01(∞,7,5) 5.∞.7.∞ | t1(∞,7,5) (7.∞)5 | t12(∞,7,5) 5.14.∞.14 | t2(∞,7,5) (7.5)∞ | t02(∞,7,5) 7.10.∞.10 | t012(∞,7,5) 10.14.∞ | s(∞,7,5) 3.5.3.7.3.∞ | |||||||||||
 (∞ 8 5) |
t0(∞,8,5) (∞.5)8 | t01(∞,8,5) 5.∞.8.∞ | t1(∞,8,5) (8.∞)5 | h1(∞,8,5) (10.4.10.∞)5 | t12(∞,8,5) 5.16.∞.16 | t2(∞,8,5) (8.5)∞ | t02(∞,8,5) 8.10.∞.10 | h02(∞,8,5) 4.4.4.5.4.∞.4.5 | t012(∞,8,5) 10.16.∞ | s(∞,8,5) 3.5.3.8.3.∞ | |||||||||
 (∞ ∞ 5) |
t0(∞,∞,5) (∞.5)∞ | t01(∞,∞,5) 5.∞.∞.∞ | t1(∞,∞,5) ∞10 | h1(∞,∞,5) (10.∞)10 | t12(∞,∞,5) 5.∞.∞.∞ | t2(∞,∞,5) (∞.5)∞ | t02(∞,∞,5) (∞.10)2 | h02(∞,∞,5) (4.∞.4.5)2 | t012(∞,∞,5) 10.∞.∞ | s(∞,∞,5) 3.5.3.∞.3.∞ | |||||||||
 (∞ 6 6) |
t0(∞,6,6) (∞.6)6 | h0(∞,6,6) (12.∞.12.3)6 | t01(∞,6,6) (6.∞)2 | h01(∞,6,6) (4.3.4.∞)2 | t1(∞,6,6) (6.∞)6 | h1(∞,6,6) (12.3.12.∞)6 | t12(∞,6,6) 6.12.∞.12 | h12(∞,6,6) 4.3.4.6.4.∞.4.6 | t2(∞,6,6) 6∞ | h2(∞,6,6) (∞.3)∞ | t02(∞,6,6) 6.12.∞.12 | h02(∞,6,6) 4.3.4.6.4.∞.4.6 | t012(∞,6,6) 12.12.∞ | s(∞,6,6) 3.6.3.6.3.∞ | |||||
 (∞ 7 6) |
t0(∞,7,6) (∞.6)7 | h0(∞,7,6) (14.∞.14.3)7 | t01(∞,7,6) 6.∞.7.∞ | t1(∞,7,6) (7.∞)6 | t12(∞,7,6) 6.14.∞.14 | h12(∞,7,6) 4.3.4.7.4.∞.4.7 | t2(∞,7,6) (7.6)∞ | t02(∞,7,6) 7.12.∞.12 | t012(∞,7,6) 12.14.∞ | s(∞,7,6) 3.6.3.7.3.∞ | |||||||||
 (∞ 8 6) |
t0(∞,8,6) (∞.6)8 | h0(∞,8,6) (16.∞.16.3)8 | t01(∞,8,6) 6.∞.8.∞ | h01(∞,8,6) 4.3.4.∞.4.4.4.∞ | t1(∞,8,6) (8.∞)6 | h1(∞,8,6) (12.4.12.∞)6 | t12(∞,8,6) 6.16.∞.16 | h12(∞,8,6) 4.3.4.8.4.∞.4.8 | t2(∞,8,6) (8.6)∞ | h2(∞,8,6) (∞.4.∞.3)∞ | t02(∞,8,6) 8.12.∞.12 | h02(∞,8,6) 4.4.4.6.4.∞.4.6 | t012(∞,8,6) 12.16.∞ | s(∞,8,6) 3.6.3.8.3.∞ | |||||
 (∞ ∞ 6) |
t0(∞,∞,6) (∞.6)∞ | h0(∞,∞,6) (∞.∞.∞.3)∞ | t01(∞,∞,6) 6.∞.∞.∞ | h01(∞,∞,6) 4.3.4.∞.4.∞.4.∞ | t1(∞,∞,6) ∞12 | h1(∞,∞,6) (12.∞)12 | t12(∞,∞,6) 6.∞.∞.∞ | h12(∞,∞,6) 4.3.4.∞.4.∞.4.∞ | t2(∞,∞,6) (∞.6)∞ | h2(∞,∞,6) (∞.∞.∞.3)∞ | t02(∞,∞,6) (∞.12)2 | h02(∞,∞,6) (4.∞.4.6)2 | t012(∞,∞,6) 12.∞.∞ | s(∞,∞,6) 3.6.3.∞.3.∞ | |||||
 (∞ 7 7) |
t0(∞,7,7) (∞.7)7 | t01(∞,7,7) (7.∞)2 | t1(∞,7,7) (7.∞)7 | t12(∞,7,7) 7.14.∞.14 | t2(∞,7,7) 7∞ | t02(∞,7,7) 7.14.∞.14 | t012(∞,7,7) 14.14.∞ | s(∞,7,7) 3.7.3.7.3.∞ | |||||||||||
 (∞ 8 7) |
t0(∞,8,7) (∞.7)8 | t01(∞,8,7) 7.∞.8.∞ | t1(∞,8,7) (8.∞)7 | h1(∞,8,7) (14.4.14.∞)7 | t12(∞,8,7) 7.16.∞.16 | t2(∞,8,7) (8.7)∞ | t02(∞,8,7) 8.14.∞.14 | h02(∞,8,7) 4.4.4.7.4.∞.4.7 | t012(∞,8,7) 14.16.∞ | s(∞,8,7) 3.7.3.8.3.∞ | |||||||||
 (∞ ∞ 7) |
t0(∞,∞,7) (∞.7)∞ | t01(∞,∞,7) 7.∞.∞.∞ | t1(∞,∞,7) ∞14 | h1(∞,∞,7) (14.∞)14 | t12(∞,∞,7) 7.∞.∞.∞ | t2(∞,∞,7) (∞.7)∞ | t02(∞,∞,7) (∞.14)2 | h02(∞,∞,7) (4.∞.4.7)2 | t012(∞,∞,7) 14.∞.∞ | s(∞,∞,7) 3.7.3.∞.3.∞ | |||||||||
 (∞ 8 8) |
t0(∞,8,8) (∞.8)8 | h0(∞,8,8) (16.∞.16.4)8 | t01(∞,8,8) (8.∞)2 | h01(∞,8,8) (4.4.4.∞)2 | t1(∞,8,8) (8.∞)8 | h1(∞,8,8) (16.4.16.∞)8 | t12(∞,8,8) 8.16.∞.16 | h12(∞,8,8) 4.4.4.8.4.∞.4.8 | t2(∞,8,8) 8∞ | h2(∞,8,8) (∞.4)∞ | t02(∞,8,8) 8.16.∞.16 | h02(∞,8,8) 4.4.4.8.4.∞.4.8 | t012(∞,8,8) 16.16.∞ | s(∞,8,8) 3.8.3.8.3.∞ | |||||
 (∞ ∞ 8) |
t0(∞,∞,8) (∞.8)∞ | h0(∞,∞,8) (∞.∞.∞.4)∞ | t01(∞,∞,8) 8.∞.∞.∞ | h01(∞,∞,8) 4.4.4.∞.4.∞.4.∞ | t1(∞,∞,8) ∞16 | h1(∞,∞,8) (16.∞)16 | t12(∞,∞,8) 8.∞.∞.∞ | h12(∞,∞,8) 4.4.4.∞.4.∞.4.∞ | t2(∞,∞,8) (∞.8)∞ | h2(∞,∞,8) (∞.∞.∞.4)∞ | t02(∞,∞,8) (∞.16)2 | h02(∞,∞,8) (4.∞.4.8)2 | t012(∞,∞,8) 16.∞.∞ | s(∞,∞,8) 3.8.3.∞.3.∞ | |||||
 (∞ ∞ ∞) |
t0(∞,∞,∞) ∞∞ | h0(∞,∞,∞) (∞.∞)∞ | t01(∞,∞,∞) (∞.∞)2 | h01(∞,∞,∞) (4.∞.4.∞)2 | t1(∞,∞,∞) ∞∞ | h1(∞,∞,∞) (∞.∞)∞ | t12(∞,∞,∞) (∞.∞)2 | h12(∞,∞,∞) (4.∞.4.∞)2 | t2(∞,∞,∞) ∞∞ | h2(∞,∞,∞) (∞.∞)∞ | t02(∞,∞,∞) (∞.∞)2 | h02(∞,∞,∞) (4.∞.4.∞)2 | t012(∞,∞,∞) ∞3 | s(∞,∞,∞) (3.∞)3 | |||||
Литература
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — 2008. — С. Chapter 19, The Hyperbolic Archimedean Tessellations. — ISBN 978-1-56881-220-5.
Ссылки
- Hatch, Don. Hyperbolic Planar Tessellations. Дата обращения: 19 августа 2010.
- Eppstein, David. The Geometry Junkyard: Hyperbolic Tiling. Дата обращения: 19 августа 2010.
- Joyce, David. Hyperbolic Tessellations. Дата обращения: 19 августа 2010.
- Richard Klitzing, 2D Tesselations, Hyperbolic Tesselations