Подстановки плиток

Подстановка плитки описывается множеством протоплиток ${\displaystyle T_{1},T_{2},\dots ,T_{m}}$, отображением расширения ${\displaystyle Q}$ и правилом деления, задающим, каким образом делить расширенные протоплитки ${\displaystyle QT_{i}}$ чтобы образовать копии некоторых протоплиток ${\displaystyle T_{j}}$. Итеративная подстановка плиток образует мозаику на плоскости, называемую подстановочной мозаикой. Некоторые подстановочные мозаики периодичны, то есть имеют трансляционную симметрию. Среди непериодических подстановочных мозаик некоторые являются апериодичными, что означает, что их протоплитки нельзя разместить в виде периодической мозаики.

Простой пример создания периодичного замощения одной плиткой, а именно, квадратом:

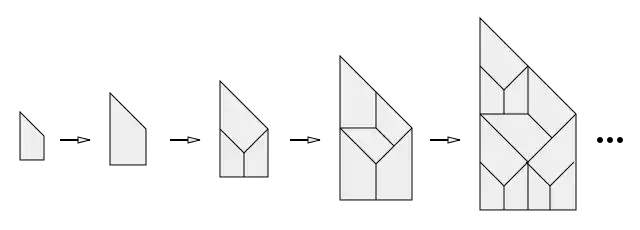
Повторяя эту подстановку, всё большие и большие области плоскости будут покрываться квадратной сеткой. Более сложный пример из двух протоплиток показан ниже.

Можно интуитивно понять, каким образом эта процедура образует подстановочную мозаику всей плоскости. Математическое определение дано ниже. Подстановочные мозаики весьма полезны как путь определения апериодичных мозаик, которые являются объектами исследования многих областей математики, включая теорию автоматов, комбинаторику, комбинаторную геометрию, динамические системы, теорию групп, гармонический анализ и теорию чисел, не говоря уже об областях, где эти мозаики возникли, кристаллографию и химию. В частности, мозаика Пенроуза является примером апериодичной подстановочной мозаики.

В 1973 и 1974 Роджер Пенроуз открыл семейство апериодических мозаик, ныне называемых мозаиками Пенроуза. Первое открытие было дано в терминах «правил совмещения», по которым работа с плитками шла так же, как с кусочками мозаичной картинки. Доказательство, что копии этих протоплиток можно соединить вместе для образования мозаики плоскости, но эта мозаика не может образовать периодическую мозаику, использует построение, которое можно рассматривать как подстановочную мозаику протоплиток. В 1977 Роберт Амманн обнаружил несколько наборов апериодических протоплиток, т.е. протоплиток, для которых правила совмещения приводят к непериодическим мозаикам. В частности, он переоткрыл первый пример Пенроуза. Этот труд повлиял на учёных, работающих в области кристаллографиия, что, в итоге, привело к открытию квазикристаллов. И наоборот, интерес к квазикристаллам привёл к открытию некоторых вполне упорядоченных апериодических мозаик. Многие из них можно легко описать как подстановочную мозаику.

Рассмотрим области в ${\displaystyle {\mathbb {R} }^{d}}$, которые хорошо обусловлены, в том смысле, что область является непустым компактным подмножеством, которое является замыканием своей внутренности.

Возьмём набор областей ${\displaystyle \mathbf {P} =\{T_{1},T_{2},\dots ,T_{m}\}}$ в качестве протоплиток. Размещение протоплитки ${\displaystyle T_{i}}$ — это пара ${\displaystyle (T_{i},\varphi )}$, где ${\displaystyle \varphi }$ является изометрией ${\displaystyle {\mathbb {R} }^{d}}$. Образ ${\displaystyle \varphi (T_{i})}$ называется областью размещения. Мозаика T — это набор областей размещения протоплиток, в котором внутренние области протоплиток не имеют общих частей. Мы говорим, что мозаика T является мозаикой на W, если W является объединение областей размещения из T.

Подстановка плиток в литературе зачастую недостаточно хорошо определена. Точное определение следующее[1].

Подстановка плитки для протоплиток P — это пара ${\displaystyle (Q,\sigma )}$, где ${\displaystyle Q:{\mathbb {R} }^{d}\to {\mathbb {R} }^{d}}$ является линейным отображением, все cобственные значения которого больше единицы по модулю, а правила подстановки ${\displaystyle \sigma }$ отображают ${\displaystyle T_{i}}$ в плитку ${\displaystyle QT_{i}}$. Подстановка плитки ${\displaystyle \sigma }$ порождает отображение из любой плитки T области W в плитку ${\displaystyle \sigma (\mathbf {T} )}$ области ${\displaystyle Q_{\sigma }(\mathbf {W} )}$

${\displaystyle \sigma (\mathbf {T} )=\bigcup _{(T_{i},\varphi )\in \mathbf {T} }\{(T_{j},Q\circ \varphi \circ Q^{-1}\circ \rho ):(T_{j},\rho )\in \sigma (T_{i})\}.}$

Заметим, что протоплитки можно вывести из подстановки плиток. Таким образом, нет необходимости включать их в подстановки плиток ${\displaystyle (Q,\sigma )}$ [2].

Любое замощение ${\displaystyle {\mathbb {R} }^{d}}$, любая конечная часть которого конгруэнтна подмножеству некоторого ${\displaystyle \sigma ^{k}(T_{i})}$, называется подстановочной мозаикой (для подстановки плитки ${\displaystyle (Q,\sigma )}$).

• Мозаика «Вертушка»

• N. Pytheas Fogg. Substitutions in dynamics, arithmetics and combinatorics / Editors Berthé, Valérie; Ferenczi, Sébastien; Mauduit, Christian; Siegel, A.. — Berlin: Springer-Verlag, 2002. — Т. 1794. — (Lecture Notes in Mathematics). — ISBN 3-540-44141-7.
• D. Frettlöh. Duality of Model Sets Generated by Substitutions // Romanian J. of Pure and Applied Math. — 2005. — Вып. 50.
• Vince A. Directions in Mathematical Quasicrystals / M. Baake, R.V. Moody. — Providence: AMS, 2000. — Т. 13. — (CRM Monograph series).

• Dirk Frettlöh's and Edmund Harriss's Encyclopedia of Substitution Tilings