Изоэдральное тело

Изоэдральный многогранник (также гранетранзитивный многогранник) размерности 3 или выше — это многогранник, все грани которого одинаковы, также удовлетворяющий некоторым дополнительным ограничениям. Более точно, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны принадлежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая переводит A в B. По этой причине правильные игральные кости имеют форму выпуклых изоэдральных многогранников[1].

Изоэдральные многогранники называются изоэдрами. Они могут быть описаны их конфигурацией граней. Изоэдральное тело, имеющее правильные вершины, является также рёберно транзитивным телом (изотоксальным) и говорят, что оно является квазиправильным двойственным — некоторые теоретики считают эти тела истинно квазиправильными, посокольку они сохраняют те же симметрии, но это принимают не все исследователи.

Изоэдральный многогранник имеет двойственный многогранник, являющийся вершинно транзитивным (изогональным). Каталановы тела, бипирамиды и трапецоэдры все изоэдральны. Они дуальны изогональным архимедовым телам, призмам и антипризмам соответственно. Правильные многогранники, которые либо самодвойственны, либо двойственны другим платоновым телам (правильным многогранникам), вершинно-, рёберно- и гранетранзитивны (изогональны, изотоксальны и изоэдральны). Изоэдральный и изогональный многогранник одновременно называется благородным многогранником.

Примеры

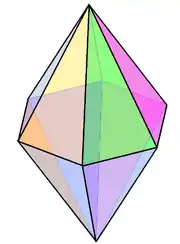Шестиугольная бипирамида V4.4.6 является примером неправильного изоэдрального многогранника.
Изоэдральная каирская пятиугольная мозаика, V3.3.4.3.4
Ромбододекаэдральные соты являются примером изоэдральных (и изохорных) заполняющих пространство сот.

k-изоэдральное тело

Многогранник является k-изоэдральным, если он содержит k граней в его фундаментальной области симметрии[2].

Аналогично, k-изоэдральная мозаика имеет k отдельных орбит симметрии (и может содержать m граней различной формы для некоторого m < k)[3].

Моноэдральный (имеющий грани одного вида) многогранник или моноэдральная мозаика (m=1) имеют конгруэнтные грани. r-эдральный многогранник или мозаика имеет r типов граней (они также называются диэдральными, триэдральными и так далее для m=2, 3, …)[4].

Несколько примеров k-изоэдральных многогранников и мозаик с раскраской граней в k симметричных позициях:

3-изоэдральный 4-изоэдральный изоэдральный 2-изоэдральный
(2-эдральные) многогранники с правильными гранями Моноэдральные многогранники
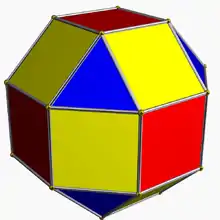
Ромбокубооктаэдр имеет один тип треугольников и два типа квадратов Удлинённый квадратный гирокупол имеет один тип треугольников и три типа квадратов. Дельтоидальный икоситетраэдр имеет один тип граней. Псевдодельтоидальный икоситетраэдр имеет 3 типа граней.
2-изоэдральная 4-изоэдральная изоэдральная 3-изоэдральная
(2-эдрадьные) мозаики с правильными гранями Монождральные мозаики
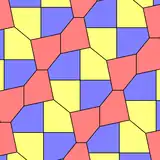Пифагорова мозаика имеет квадраты 2 размеров. 3-однородная мозаика имеет 3 типа одинаковых треугольников и квадраты одного вида. Узор «ёлочкой» имеет правильные грани одного типа. Пятиугольная мозаика имеет 3 типа идентичных неправильных пятиугольных граней.

Связанные понятия

Ячейно транзитивное или изохорное тело является n-мерным многогранником (n>3) или сотами, которые имеют конгруэнтные и переходящие друг в друга с помощью симметрии (то есть транзитивные) ячейки.

Гранетранзитивное или изотопное тело (изотоп) является n-мерной фигурой или сотами с конгруэнтными и транзитивными фасетами ((n-1)-гранями). Двойственный многогранник изотопа является изогональным многогранником. По определению, это изотопное свойство является общим для двойственных тел однородных многогранников.

  • Изотопная 2-мерная фигура является изотоксальной (рёбернотранзитивной).
  • Изотопное 3-мерное тело является изоэдральным (гранетранзитивным).
  • Изотопное 4-мерное тело является изохорным (ячейнотранзитивным).

См. также

Примечания
  1. McLean, 1990, с. 243–256.
  2. Socolar, 2007, с. 33–38.
  3. Kaplan, 2009, с. 35.
  4. Grünbaum, Shephard, 1987, с. 20, 23.

Литература

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.