Список плоских групп симметрии
В статье суммируется информация о классах дискретных групп симметрии евклидовой плоскости. Группы симметрии, приведённые здесь, именуются по трём схемам именования: международная нотация, орбифолдная нотация и нотация Коксетера. Существует три вида групп симметрии на плоскости:
- 2 бесконечных семейства точечных групп
- 7 групп бордюра – 2D-рёберные группы
- 17 групп обоев – 2D-пространственные группы.
Точечные группы симметрии
На плоскости имеется точка, инвариантная относительно каждого преобразования. Существует два бесконечных семейства дискретных двумерных точечных групп. Группы определяются параметром n, равным порядку подгруппы вращений. Также параметр n равен показателю группы.
| Семейство | Межд. (орбифолд) |
Шёнфлиса | Геом. [1] Коксетер |
Порядок | Примеры | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Циклические группы | n (n•) |
Cn | n [n]+ |
n |  C1, [ ]+ (•) |
 C2, [2]+ (2•) |
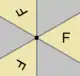 C3, [3]+ (3•) |
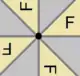 C4, [4]+ (4•) |
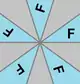 C5, [5]+ (5•) |
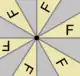 C6, [6]+ (6•) |
| Диэдральные группы | nm (*n•) |
Dn | n [n] |
2n |  D1, [ ] (*•) |
 D2, [2] (*2•) |
 D3, [3] (*3•) |
 D4, [4] (*4•) |
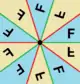 D5, [5] (*5•) |
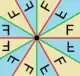 D6, [6] (*6•) |
Группа бордюров
На плоскости имеется прямая, которая переходит в себя при каждом преобразовании. При этом отдельные точки этой прямой могут не оставаться неподвижными.
7 групп бордюров, двумерных рёберных групп. Символы Шёнфлиса даны как бесконечные пределы 7 диэдральных групп. Жёлтые области представляют бесконечные фундаментальные области для каждого бордюра.
| IUC (орбифолд) |
Геом. | Шёнфлис | Коксетер | Фундаментальная область |
Пример |
|---|---|---|---|---|---|
| p1 (∞•) | p1 | C∞ | [1,∞]+ |  | |
| p1m1 (*∞•) | p1 | C∞v | [1,∞] |  |
| IUC (Орбифолд) |
Геом. | Шёнфлис | Коксетер | Фундаментальная область |
Пример |
|---|---|---|---|---|---|
| p11g (∞×) | p.g1 | S2∞ | [2+,∞+] | 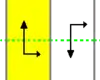 | |
| p11m (∞*) | p. 1 | C∞h | [2,∞+] |  |
| IUC (Орбифолд) |
Геом. | Шёнфлис | Коксетер | Фундаментальная область |
Пример |
|---|---|---|---|---|---|
| p2 (22∞) | p2 | D∞ | [2,∞]+ | 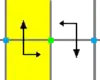 | |
| p2mg (2*∞) | p2g | D∞d | [2+,∞] |  | |
| p2mm (*22∞) | p2 | D∞h | [2,∞] |  |
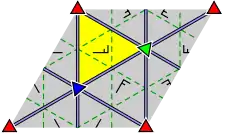
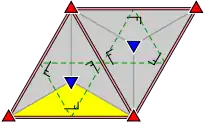
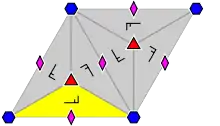
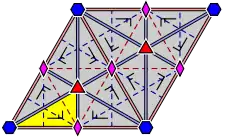
Группы обоев
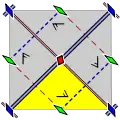
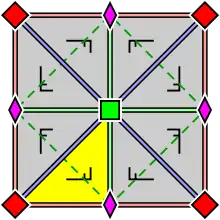
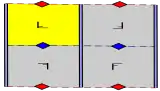
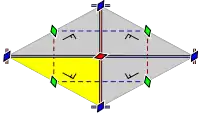
17 групп обоев с конечными фундаментальными областями, упорядоченные по международной нотации, орбифолдной нотации и нотации Коксетера и классифицированы 5 решётками Браве на плоскости: квадратной, скошенной (параллелограммной), шестиугольной (ромбы с углами 60 градусов), прямоугольной и ромбической.
Группы p1 и p2 с зеркальной симметрией встречаются во всех классах. Связанная чистая группа Коксетера отражений дана для всех классов, за исключением косых.
|
|
|
|
Взаимосвязь подгрупп обоев
В приведенной ниже таблице на пересечении строки, соответствующей группе , и столбца, соответствующего группе , находится минимальный индекс подгруппы , изоморфной . На диагонали находится минимальный индекс собственной подгруппы, изоморфной объемлющей группе.
| o | 2222 | ×× | ** | *× | 22× | 22* | *2222 | 2*22 | 442 | 4*2 | *442 | 333 | *333 | 3*3 | 632 | *632 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p1 | p2 | pg | pm | cm | pgg | pmg | pmm | cmm | p4 | p4g | p4m | p3 | p3m1 | p31m | p6 | p6m | ||
| o | p1 | 2 | ||||||||||||||||
| 2222 | p | 2 | 2 | 2 | ||||||||||||||
| ×× | pg | 2 | 2 | |||||||||||||||
| ** | pm | 2 | 2 | 2 | 2 | |||||||||||||
| *× | cm | 2 | 2 | 2 | 3 | |||||||||||||
| 22× | pgg | 4 | 2 | 2 | 3 | |||||||||||||
| 22* | pmg | 4 | 2 | 2 | 2 | 4 | 2 | 3 | ||||||||||
| *2222 | pmm | 4 | 2 | 4 | 2 | 4 | 4 | 2 | 2 | 2 | ||||||||
| 2*22 | cmm | 4 | 2 | 4 | 4 | 2 | 2 | 2 | 2 | 4 | ||||||||
| 442 | p4 | 4 | 2 | 2 | ||||||||||||||
| 4*2 | p4g | 8 | 4 | 4 | 8 | 4 | 2 | 4 | 4 | 2 | 2 | 9 | ||||||
| *442 | p4m | 8 | 4 | 8 | 4 | 4 | 4 | 4 | 2 | 2 | 2 | 2 | 2 | |||||
| 333 | p3 | 3 | 3 | |||||||||||||||
| *333 | p3m1 | 6 | 6 | 6 | 3 | 2 | 4 | 3 | ||||||||||
| 3*3 | p31m | 6 | 6 | 6 | 3 | 2 | 3 | 4 | ||||||||||
| 632 | p6 | 6 | 3 | 2 | 4 | |||||||||||||
| *632 | p6m | 12 | 6 | 12 | 12 | 6 | 6 | 6 | 6 | 3 | 4 | 2 | 2 | 2 | 3 |
См. также
- Список групп сферической симметрии
- Гиперболическая плоскость — Гиперболические группы симметрии
Примечания
- Hestenes, Holt, 2007.
- H. S. M. Coxeter, W. O. J. Moser. Generators and Relations for Discrete Groups. Berlin:Springer, 1972. § 4.6, Table 4
Литература
- D. Hestenes, J. Holt. The Crystallographic Space groups in Geometric algebra // Journal of Mathematical Physics.. — 2007. — Т. 48, 023514.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — A.K. Peters, 2008. — ISBN 978-1-56881-220-5. (Orbifold notation for polyhedra, Euclidean and hyperbolic tilings)
- John H. Conway, Derek A. Smith. On Quaternions and Octonions: Their geometry, arithmetic, and symmetry. — Natick, MA: A K Peters, Ltd., 2003. — ISBN 978-1-56881-134-5.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- Coxeter, H. S. M. and Moser, W. O. J. Generators and Relations for Discrete Groups. — New York: Springer-Verlag, 1980. — ISBN 0-387-09212-9.
- N.W. Johnson. Chapter 11: Finite symmetry groups // Geometries and Transformations. — 2015.
Ссылки
- "Conway's manuscript" on Orbifold notation (Notation changed from this original, x is now used in place of open-dot, and o is used in place of the closed dot)
- The 17 Wallpaper Groups