Шестиугольник

Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы.

Площадь шестиугольника без самопересечений

Площадь шестиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.

Выпуклый шестиугольник

Выпуклым шестиугольником называется шестиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Сумма внутренних углов выпуклого шестиугольника равна 720°.

\sum _{i=1}^{6}\alpha _{i}=(6-2)\cdot 180^{\circ }=4\cdot 180^{\circ }=720^{\circ }

Доказано[1], что в любом достаточно большом множестве точек в общем положении содержится выпуклый пустой (то есть не содержащий точек этого множества) шестиугольник. Но существуют сколь угодно большие множества точек в общем положении, в которых нет выпуклого пустого семиугольника[2]. Вопрос о необходимом числе точек по сей день остаётся открытым. Известно, что требуется не менее 30 точек[3]. А если справедлива гипотеза Эрдёша-Секереша о многоугольниках, то не более 129[4].

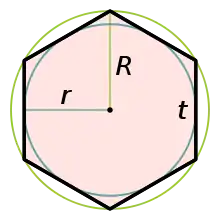
Правильный шестиугольник

Правильным называется шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Гексаграмма

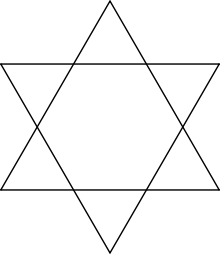
Звездчатые шестиугольники

Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника, называется звёздчатым. Помимо правильного существует ещё один звёздчатый шестиугольник, состоящий из двух правильных треугольников — гексаграмма или звезда Давида.

См. также

Примечания

Nicolás, Carlos M. (2007), The empty hexagon theorem, Discrete and Computational Geometry Т. 38 (2): 389–397, DOI 10.1007/s00454-007-1343-6
Horton, J. D. (1983), Sets with no empty convex 7-gons, Canadian Mathematical Bulletin Т. 26 (4): 482–484, DOI 10.4153/CMB-1983-077-8
Overmars, M. (2003), Finding sets of points without empty convex 6-gons, Discrete and Computational Geometry Т. 29 (1): 153–158, DOI 10.1007/s00454-002-2829-x
Gerken, Tobias (2008), Empty convex hexagons in planar point sets, Discrete and Computational Geometry Т. 39 (1–3): 239–272, DOI 10.1007/s00454-007-9018-x

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Nicolás, Carlos M. (2007), The empty hexagon theorem, Discrete and Computational Geometry Т. 38 (2): 389–397, DOI 10.1007/s00454-007-1343-6

[2] Horton, J. D. (1983), Sets with no empty convex 7-gons, Canadian Mathematical Bulletin Т. 26 (4): 482–484, DOI 10.4153/CMB-1983-077-8

[3] Overmars, M. (2003), Finding sets of points without empty convex 6-gons, Discrete and Computational Geometry Т. 29 (1): 153–158, DOI 10.1007/s00454-002-2829-x

[4] Gerken, Tobias (2008), Empty convex hexagons in planar point sets, Discrete and Computational Geometry Т. 39 (1–3): 239–272, DOI 10.1007/s00454-007-9018-x