Дельтоид

Дельто́ид (от др.-греч. δελτοειδής — «дельтовидный», напоминающий заглавную букву дельта) — четырёхугольник, четыре стороны которого можно сгруппировать в две пары равных смежных сторон.

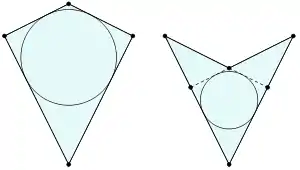
На чертеже слева дельтоид выпуклый, справа — невыпуклый.

Свойства

Свойства дельтоида

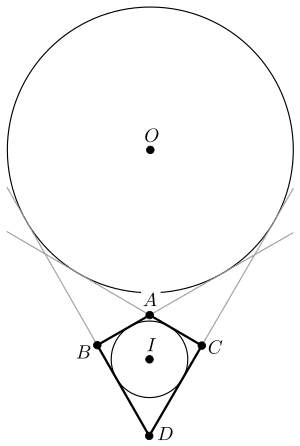
Вписанная и вневписанная окружности выпуклого дельтоида

ABCD

.

Углы между сторонами неравной длины равны.
Диагонали взаимно перпендикулярны.
В любой выпуклый дельтоид можно вписать окружность; кроме того, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон (см. рисунок).
Для любого невыпуклого дельтоида можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон, и окружность, касающуюся двух меньших сторон и продолжений двух бо́льших сторон.
Точка пересечения диагоналей делит одну из них пополам.
Другая диагональ является биссектрисой углов.
Одна диагональ делит дельтоид на два равных треугольника.
Другая диагональ делит дельтоид на два равнобедренных треугольника, если он выпуклый, и достраивает его равнобедренным треугольником до равнобедренного треугольника, если он невыпуклый.

Площадь дельтоида

Здесь приведены формулы, свойственные именно дельтоиду. См. также формулы для площади произвольных четырёхугольников.

S={\frac {d_{1}d_{2}}{2}}

, где

d_{1}

и

d_{2}

— длины диагоналей.

S={ab\sin \alpha }

, где

a

и

b

— длины неравных сторон, а

\alpha

— угол между ними.

Частные случаи

Если угол между неравными сторонами дельтоида прямой, то вокруг него можно описать окружность (вписанный дельтоид).
Если пара противоположных сторон дельтоида равна, то такой дельтоид является ромбом.
Если пара противоположных сторон и обе диагонали дельтоида равны, то дельтоид является квадратом. Квадратом является и вписанный дельтоид с равными диагоналями.

Разное

Дельтоидами являются грани дельтоидального икоситетраэдра, дельтоидального гексеконтаэдра и трапецоэдра.

См. также

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.