Неравенство Птолемея
Неравенство Птолемея — неравенство на 6 расстояний между четвёркой точек на плоскости.
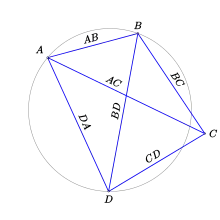
Если 4 точки не лежат на одной окружности, то все три неравенства Птолемея строгие.
Названо в честь позднеэллинистического математика Клавдия Птолемея.
Формулировка
Для любых точек плоскости выполнено неравенство
причём равенство достигается тогда и только тогда, когда — выпуклый вписанный четырёхугольник, или точки лежат на одной прямой.
Замечания
- Случай равенства также называется тождеством Птолемея.
О доказательствах
- Один из вариантов доказательства неравенства основан на применении инверсии относительно окружности с центром в точке ; этим неравенство Птолемея сводится к неравенству треугольника для образов точек , , .[1]
- Существует способ доказательства через прямую Симсона.
- Теорема Птолемея может доказываться следующим способом (близким к доказательству самого Птолемея, приведённому им в книге Альмагест) — ввести точку такую, что , а потом через подобие треугольников.
- Теорема также является следствием из соотношения Бретшнайдера.
Следствия
- Теорема Помпею.[2] Рассмотрим точку и правильный треугольник . Тогда из отрезков , и можно составить треугольник, причём этот треугольник вырожденный тогда и только тогда, когда точка лежит на описанной окружности треугольника .
Вариации и обобщения
- Соотношение Бретшнайдера
- Неравенства Птолемея можно распространить и на шесть точек: если произвольные точки плоскости (это обобщение называют теоремой Птолемея для шестиугольника, а в зарубежной литературе теоремой Фурмана (Fuhrmann’s theorem)[3]), то
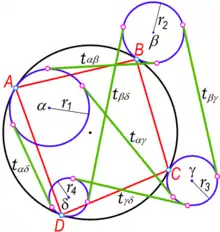 Обобщенная теорема Птолемея или теорема Кейси
Обобщенная теорема Птолемея или теорема Кейси
- причем равенство достигается тогда и только тогда, когда — вписанный шестиугольник.
- Теорема Кейси (обобщённая теорема Птолемея): Рассмотрим окружности и , касающиеся данной окружности в вершинах и выпуклого четырёхугольника . Пусть — длина общей касательной к окружностям и (внешней, если оба касания внутренние или внешние одновременно, и внутренней, если одно касание внутреннее, а другое внешнее); и т. д. определяются аналогично. Тогда
- .
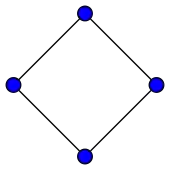
Циклический граф, в котором все расстояния удовлетворяют неравенству Птолемея, называют графом Птолемея
- Граф Птолемея (см. рис.)[4],
Примечания
- Доказательство теоремы Птолемея с помощью инверсии Архивная копия от 26 мая 2009 на Wayback Machine. Дистанционный консультационный пункт по математике МЦНМО.
- О теореме Д. Помпейю Архивная копия от 17 декабря 2004 на Wayback Machine. Дистанционный консультационный пункт по математике МЦНМО.
- Теорема Птолемея. Дата обращения: 17 мая 2011. Архивировано 26 мая 2009 года.
- Howorka, Edward (1981), A characterization of Ptolemaic graphs (Характеризация графов Птолемея), Journal of Graph Theory Т. 5 (3): 323–331, DOI 10.1002/jgt.3190050314.
Литература
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 328-329. — 383 с. — ISBN 5-09-001287-3.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 61-63. — ISBN 5-94057-170-0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.