Неравенство треугольника
Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда меньше суммы длин двух его других сторон. Неравенство треугольника включается как аксиома в определение метрического пространства, нормы и т.д.; также, часто является теоремой в различных теориях.
Евклидова геометрия
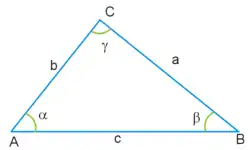
Неравенство
выполняется в любом треугольнике . Причём равенство достигается только тогда, когда треугольник вырожден, и точка лежит строго между и .
Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из неё выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника.
Доказательство
Рассмотрим произвольный треугольник .

Докажем, что .
На продолжении стороны отложим отрезок равный стороне . Полученный треугольник равнобедренный, значит
-
(1)
Рассмотрим треугольник .
В этом треугольнике — это часть , поэтому:
-
(2)
Учитывая (1), получаем:
-
(3)
По теореме о соотношении между углами и сторонами треугольника [1], против большего угла треугольника лежит большая сторона.
Следовательно в треугольнике имеет место неравенство:
-
(4)
Кроме того:
-
(5)
Из (4) и (5) получаем искомое:
Нормированное пространство
Пусть — нормированное векторное пространство, где — произвольное множество, а — определённая на норма. Тогда по определению последней справедливо:
Гильбертово пространство
В гильбертовом пространстве, неравенство треугольника является следствием неравенства Коши — Буняковского.
Метрическое пространство
Пусть — метрическое пространство, где — произвольное множество, а — определённая на метрика. Тогда по определению последней
Вариации и обобщения
Обратное неравенство треугольника
Следствием неравенства треугольника в нормированном и метрическом пространствах являются следующие неравенства:
Неравенство треугольника для трёхгранного угла
Каждый плоский угол выпуклого трёхгранного угла меньше суммы двух других его плоских углов.
Произвольное число точек
Обозначим расстояние между точками и . Тогда имеет место следующее неравенство: . Оно получается последовательным применением неравенства треугольника для трех точек: [2]
См. также
Примечания
- Теорема о соотношении между углами и сторонами треугольника. Мир математики. Дата обращения: 19 декабря 2021. Архивировано 19 декабря 2021 года.
- Шилов Г. Е. Математический анализ. Специальный курс. — М.: Физматлит, 1961. — C. 28