Равногранный тетраэдр

Тетраэдр называется равногранным, если все его грани — равные между собой треугольники.

Существует ряд эквивалентных определений равногранного тетраэдра:

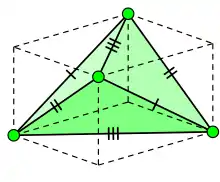
Равногранный тетраэдр с описанным прямоугольным параллелепипедом.

1. описанный около него параллелепипед — прямоугольный;
2. его развёртка, полученная при разрезании его по трём сходящимся в одной вершине рёбрам, — треугольник (этот треугольник должен быть остроугольным, потому что тупоугольный или прямоугольный при сгибании по средним линиям не сложится в тетраэдр);
3. его развёртка, полученная при разрезании ломаной из трёх звеньев, — параллелограм;
4. у него имеется три оси симметрии — это общие перпендикуляры, проведённые к противоположным рёбрам, они же бимедианы;
5. все его трёхгранные углы равны
6. сумма углов треугольников при каждой вершине равна ${\displaystyle \pi }$);
7. сумма косинусов двугранных углов при каждой вершине равна 1;
8. все его медианы равны;
9. все его высоты равны;
10. центры вписанной и описанной сфер и центроид совпадают;
11. радиусы окружностей описанных около граней равны;
12. периметры граней равны;
13. площади граней равны;
14. противоположные двугранные углы равны;
15. противоположные рёбра равны;
16. центры вневписанных сфер лежат на описанной сфере;
17. среди выпуклых многогранников, равногранные тетраэдры и только они допускают произвольно длинные замкнутые геодезические без самопересечений на своих поверхностях;[4] (То же свойство выделяет равногранные тетраэдры среди всех замкнутых выпуклых поверхностей.[5])
18. тетраэдр ${\displaystyle ABCD}$ является равногранным если и только если выполняется равенство ${\displaystyle (a+b-c)(a+c-b)(b+c-a)=72V^{2}}$. Здесь ${\displaystyle a=AB\cdot CD}$, ${\displaystyle b=AC\cdot BD}$, ${\displaystyle c=AD\cdot BC}$, и ${\displaystyle V}$— объём тетраэдра ${\displaystyle ABCD}$.[6]

• В. Александров. Вращающееся кольцо тетраэдров «Квант», № 5, 2001 г. С.31.
• В. В. Прасолов, И. Ф. Шарыгин Задачи по стереометрии. М.: Наука, 1989. 288 с ISBN 5-02-013921-1; Тираж 163000 экз. Серия Библиотека математического кружка, выпуск 19.