Перестановочный многогранник
В математике перестановочный многогранник порядка n — это (n − 1)-мерный выпуклый многогранник, вложенный в n-мерное евклидово пространство, который является выпуклой оболочкой всех n! точек, получающихся перестановками координат вектора (1, 2, 3, …, n).
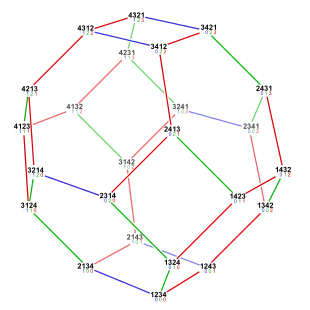
История
Согласно Циглер, Гюнтер[1], перестановочный многогранник впервые появляется в работах Шутэ в 1911 году. Сам термин «перестановочный многогранник» (точнее, его французский вариант «permutoèdre») впервые появился в статье Гуибуда (G.-T.Guibaud) и Розенштэхл, Пьер в 1963 году. Предлагая его, авторы писали, что «permutoèdre» выглядит варварски, но легко запоминается и что они оставляют использование этого термина на усмотрение читателя.
Близким понятием является многогранник Биркгофа, определяемый как выпуклая оболочка матриц перестановок. В более общей ситуации Боуман (V.-J.Bowman) в 1972 году использовал термин «перестановочный многогранник» («permutation polytope») для любого многогранника, вершины которого находятся во взаимно однозначном соответствии с перестановками некоторого множества.
Свойства
- Перестановочный многогранник порядка n имеет n! вершин, каждая из которых соединена с n − 1 другими вершинами, так что общее число рёбер равно (n − 1)n!/2.
- Каждое ребро имеет длину √2 и соединяет две вершины, получающиеся друг из друга перестановкой двух координат при условии, что значения этих координат различаются на единицу.[2]
- Перестановочный многогранник имеет одну гипергрань для каждого непустого собственного подмножества S множества {1, 2, 3, …, n}, состоящую из всех вершин, у которых все координаты с номерами, вошедшими в S, имеют меньшие значения, чем все координаты с номерами, не вошедшими в S. Отсюда следует, что общее число гиперграней равно 2n − 2.
- Перестановочный многогранник является вершинно-транзитивным, а именно: симметрическая группа Sn действует на множестве вершин перестановочного многогранника посредством перестановок координат.
- Перестановочный многогранник является зонотопом; параллельная копия перестановочного многогранника может быть получена как сумма Минковского n(n − 1)/2 прямолинейных отрезков, соединяющих все пары векторов стандартного базиса.[3]
- Неориентированный граф, образованный вершинами и рёбрами перестановочного многогранника, изоморфен графу Кэли симметрической группы.[1]
Замощение пространства
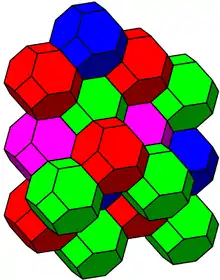
Перестановочный многогранник порядка n полностью содержится в (n − 1)-мерной гиперплоскости, состоящей из всех точек, сумма координат которых равна
- 1 + 2 + … + n = n(n + 1)/2.
Более того, эта гиперплоскость может быть замощена (англ.) бесконечным количеством параллельных копий перестановочного многогранника. Каждая из этих копий отличается от исходного перестановочного многогранника на элемент некоторой (n − 1)-мерной решётки, образованной n-мерными векторами, все координаты которых целочисленные, их сумма равна нулю, причём все координаты принадлежат одному классу вычетов по модулю n:
- x1 + x2 + … + xn = 0, x1 ≡ x2 ≡ … ≡ xn (mod n).
Например, перестановочный многогранник порядка 4, изображённый на рисунке, замощает 3-мерное пространство посредством параллельных переносов. Здесь 3-мерное пространство рассматривается как аффинное подпространство 4-мерноего пространства R4 с координатами x, y, z, w, которое образовано четвёрками вещественных чисел, сумма которых равна 10, то есть
- x + y + z + w = 10.
Легко проверить, что для каждого из следующих четырёх векторов
- (1,1,1,−3), (1,1,−3,1), (1,−3,1,1) и (−3,1,1,1),
сумма координат равна нулю и все координаты сравнимы с 1 по модулю 4. Любые три из этих векторов порождают решётку параллельных переносов.
Замощения, построенные таким способом из перестановочных многогранников порядка 3 и 4, являются замощением правильными шестиугольниками и замощением усечёнными октаэдрами (англ.) соответственно.
Галерея
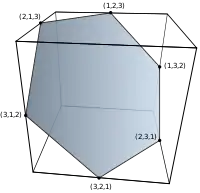
| Порядок 2 | Порядок 3 | Порядок 4 |
|---|---|---|
| 2 вершины | 6 вершин | 24 вершины |
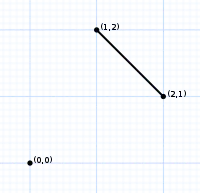 |
 |
 |
| Перестановочный многогранник порядка 2 — это отрезок на диагонали единичного квадрата. | Перестановочный многогранник порядка 3 — это правильный шестиугольник, являющийся сечением 2×2×2 куба. | Перестановочный многогранник порядка 4 — это усечённый октаэдр. |
| Порядок 5 | Порядок 6 |
|---|---|
| 120 вершин | 720 вершин |
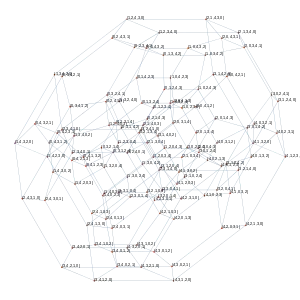 |
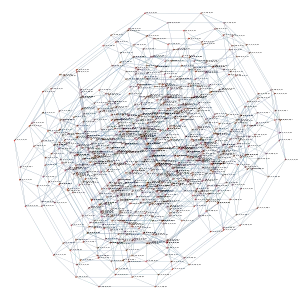 |
| Перестановочный многогранник порядка 5. | Перестановочный многогранник порядка 6. |
Замечания
- Günter M. Ziegler, `Lectures on Polytopes', Springer-Verlag, 1995.
- P.Gaiha and S. K.Gupta, `Adjacent vertices on a permutohedron', SIAM Journal on Applied Mathematics, Vol. 32, issue 2, P. 323—327 (1977).
- Günter M. Ziegler, `Lectures on Polytopes', Springer-Verlag, 1995. P. 200.
Литература
- Bowman, V. J. (1972), Permutation polyhedra, SIAM Journal on Applied Mathematics Т. 22 (4): 580–589, doi:10.1137/0122054, <http://links.jstor.org/sici?sici=0036-1399(197206)22%3A4%3C580%3APP%3E2.0.CO%3B2-P>.
- Gaiha, P. & Gupta, S. K. (1977), Adjacent vertices on a permutohedron, SIAM Journal on Applied Mathematics Т. 32 (2): 323–327, doi:10.1137/0132025, <http://links.jstor.org/sici?sici=0036-1399(197703)32%3A2%3C323%3AAVOAP%3E2.0.CO%3B2-1>.
- Guilbaud, Georges-Théodule & Rosenstiehl, Pierre (1963), Analyse algébrique d'un scrutin, Mathématiques et sciences humaines Т. 4: 9–33, <http://www.numdam.org/numdam-bin/fitem?ma=189547&id=MSH_1963__4__9_0> Архивная копия от 5 июня 2011 на Wayback Machine.
- Le Conte de Poly-Barbut, Cl. (1990), Le diagramme du treillis permutoèdre est intersection des diagrammes de deux produits directs d’ordres totaux, Mathématiques, Informatique et Sciences Humaines Т. 112: 49–53.
- Santmyer, Joe (2007), For all possible distances look to the permutohedron, Mathematics Magazine Т. 80 (2): 120–125, <http://www.ingentaconnect.com/content/maa/mm/2007/00000080/00000002/art00005>
- Schoute, Pieter Hendrik (1911), Analytic treatment of the polytopes regularly derived from the regular polytopes, Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam Т. 11 (3): 87 pp. Googlebook, 370—381
- Ziegler, Günter M. (1995), Lectures on Polytopes, Springer-Verlag, Graduate Texts in Mathematics 152
- Гарбер, А.И. & Поярков, А.П. (2006), О перестановочных многогранниках, Вестник МГУ, серия 1 (no. 2): 3–8.
Ссылки
- Bryan Jacobs. Permutohedron (англ.) на сайте Wolfram MathWorld.
- Alexander Postnikov (2005), Permutohedra, associahedra, and beyond, arΧiv:math.CO/0507163 [math.CO]