Купол (геометрия)
Купол — тело, образованное соединением двух многоугольников, в котором один (основание) имеет вдвое больше сторон по сравнению с другим (верхняя грань). Соединение многоугольников осуществляется равнобедренными треугольниками и прямоугольниками. Если треугольники правильные, а прямоугольники являются квадратами, в то время как основание и вершина являются правильными многоугольниками, купол является многогранником Джонсона. Эти куполы, трёхскатный, четырёхскатный и пятискатный, можно получить, взяв сечения кубооктаэдра, ромбокубооктаэдра и ромбоикосододекаэдра соответственно.
| Пятиугольный купол (пример) | |
|---|---|
 | |
| Тип | Множество куполов |
| Символ Шлефли | {n} || t{n} |
| Граней | n треугольников, n квадратов, 1 n-угольник, 1 2n-угольник |
| Рёбер | 5n |
| Вершин | 3n |
| Группа симметрии | Cnv, [1,n], (*nn), порядок 2n |
| Группа вращений | Cn, [1,n]+, (nn), порядок n |
| Двойственный многогранник | ? |
| Свойства | выпуклый |
Купол можно рассматривать как призму, где один из многоугольников наполовину стянут путём объединения вершин попарно.
Куполу можно приписать расширенный символ Шлефли {n} || t{n}, представляющий правильный многоугольник {n}, соединённый с параллельной ему усечённой копией, t{n} или {2n}.
Куполы являются подклассом призматоидов.
Примеры
| n | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Название | {2} || t{2} | {3} || t{3} | {4} || t{4} | {5} || t{5} | {6} || t{6} |
| Купол |  Диагональный купол |
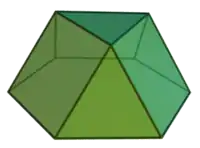 Трёхскатный купол |
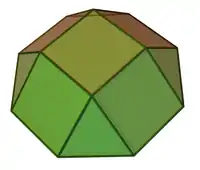 Четырёхскатный купол |
 Пятискатный купол |
 Шестискатный купол (плоский) |
| Связанные однородные многогранники |
Треугольная призма |
Кубооктаэдр |
Ромбокубо- октаэдр |
Ромбоикосо- додекаэдр |
Ромботри- шестиугольная мозаика |

Упомянутые выше три многогранника являются нетривиальными выпуклыми куполами с правильными гранями. «Шестиугольный купол» является плоской фигурой, а треугольную призму может считать «куполом» степени 2 (купол отрезка и квадрата). Однако куполы с большим числом сторон многоугольников могут быть построены только с неправильными треугольными и прямоугольными гранями.
Координаты вершин
Определение купола не требует правильности основания и верхней грани, но удобно рассматривать случаи, в которых куполы имеют максимальную симметрию, Cnv. В этом случае верхняя грань является правильным n-угольником, в то время как основание является правильным 2n-угольником, либо 2n-угольником с двумя различными длинами сторон (через одну) и теми же углами, что и у правильного 2n- угольника. Удобно расположить купол в координатной системе так, чтобы его основание лежало в плоскости xy с верхней гранью, параллельной этой плоскости. Ось z является осью симметрии порядка n, зеркальные плоскости проходят через эту ось и делят стороны основания пополам. Они также делят пополам стороны или углы верхней грани, или и то, и другое. (Если n чётно, половина зеркал делит пополам стороны, половина — углы. Если же n нечётно, каждое зеркало делит пополам одну сторону и один угол верхней грани.) Пронумеруем вершины основания числами от V1 до V2n, а вершины верхней грани — числами от V2n+1 до V3n. Координаты вершин тогда можно записать следующим образом:
- V2j−1: (rb cos[2π(j − 1) / n + α], rb sin[2π(j − 1) / n + α], 0)
- V2j: (rb cos(2πj / n − α), rb sin(2πj / n − α), 0)
- V2n+j: (rt cos(πj / n), rt sin(πj / n), h),
где j = 1, 2, …, n.
Поскольку многоугольники V1V2V2n+2V2n+1, и т. д. являются прямоугольниками, на значения rb, rt и α накладываются ограничения. Расстояние V1V2 равно
- rb{[cos(2π / n − α) − cos α]2 + [sin(2π / n − α) − sin α]2}1⁄2
- = rb{[cos2(2π / n − α) − 2cos(2π / n − α)cos α + cos2 α] + [sin2(2π / n − α) − 2sin(2π / n − α)sin α + sin2 α]}1⁄2
- = rb{2[1 − cos(2π / n − α)cos α − sin(2π / n − α)sin α]}1⁄2
- = rb{2[1 − cos(2π / n − 2α)]}1⁄2
а расстояние V2n+1V2n+2 равно
- rt{[cos(π / n) − 1]2 + sin2(π / n)}1⁄2
- = rt{[cos2(π / n) − 2cos(π / n) + 1] + sin2(π / n)}1⁄2
- = rt{2[1 − cos(π / n)]}1⁄2.
Они должны быть равны, так что, если это общее ребро имеет длину s,
- rb = s / {2[1 − cos(2π / n − 2α)]}1⁄2
- rt = s / {2[1 − cos(π / n)]}1⁄2
И эти значения следует подставить в вышеприведённые формулы для вершин.
Звёздчатые куполы
| n / d | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 |  {4/3} |
 {5/3} |
 {7/3} |
 {8/3} |
| 5 | — | — |  {7/5} |
 {8/5} |
| n / d | 3 | 5 | 7 |
|---|---|---|---|
| 2 | 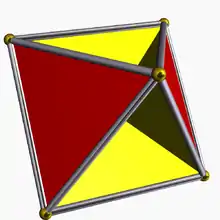 Скрещенный треугольный куполоид |
 Пентаграммный куполоид |
 Гептаграммный куполоид |
| 4 | — | 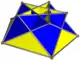 Скрещенный пентаграммный куполоид |
 Скрещенный гептаграммный куполоид |
Звёздчатые куполы существуют для всех оснований {n/d}, где 6/5 < n/d < 6 и d нечётно. На границах куполы превращаются в плоские фигуры. Если d чётно, нижнее основание {2n/d} становится вырожденным — мы можем образовать куполоид или полукупол путём удаления этой вырожденной грани и позволив треугольникам и квадратам соединяться друг с другом. В частности, тетрагемигексаэдр можно рассматривать как {3/2}-куполоид. Все куполы ориентированны, в то время как все куполоиды неориентированны. Если n/d > 2 для куполоида, треугольники и квадраты не покрывают всё основание и маленькая мембрана остаётся на основании, которая просто закрывает дыру. Таким образом, куполоиды {5/2} и {7/2} на рисунке выше имеют мембраны (не заполнены), в то время как куполоиды {5/4} и {7/4} их не имеют.
Высота h купола {n/d} или куполоида задаётся формулой . В частности, h = 0 на границах n/d = 6 и n/d = 6/5, и h максимально при n/d = 2 (треугольная призма, где треугольники расположены вертикально)[1][2].
На рисунках выше звёздчатые куполы показаны в цветах, чтобы подчеркнуть их грани — грань n/d-угольника показана красным, грань 2n/d-угольника показана жёлтым, квадраты представлены синим цветом, а треугольники — зелёным. Куполоиды имеют красные n/d-угольные грани, жёлтые квадратные грани, а треугольные грани выкрашены в голубой цвет, второе же основание удалено.
Гиперкуполы
Гиперкуполы или многогранные куполы — это семейство выпуклых неоднородных четырёхмерных многогранников, аналогичных куполам. Основаниями каждого такого многогранника являются правильный многогранник (трёхмерный) и его растяжение[3].
В таблице используется понятие Сегментогранник (англ. Segmentochora) — это фигура, удовлетворяющая следующим свойствам:
- 1. все вершины находятся на одной гиперсфере
- 2. все вершины находятся на двух параллельных гиперплоскостях
- 3. все рёбра имеют длину 1
В плоскости существует два сегментогранника (сегментоугольника) — правильный треугольник и квадрат.
В 3-мерном пространстве они включают пирамиды, призмы, антипризмы, купола.
| Название | Тетраэдральный купол | Кубический купол | Октаэдральный купол | Декаэдральный купол | Шестиугольный мозаичный купол | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Символ Шлефли | {3,3} ∨ rr{3,3} | {4,3} ∨ rr{4,3} | {3,4} ∨ rr{3,4} | {5,3} ∨ rr{5,3} | {6,3} ∨ rr{6,3} | |||||
| Индекс сегментогранника[3] |
K4.23 | K4.71 | K4.107 | K4.152 | ||||||
| Радиус описанной окружности |
1 | sqrt((3+sqrt(2))/2) = 1.485634 |
sqrt(2+sqrt(2)) = 1.847759 |
3+sqrt(5) = 5.236068 |
||||||
| Рисунок |  |
 |
 |
 |
||||||
| Главные ячейки |   |
  |
  |
  |
 
| |||||
| Вершин | 16 | 32 | 30 | 80 | ∞ | |||||
| Рёбер | 42 | 84 | 84 | 210 | ∞ | |||||
| Граней | 42 | 24 {3} + 18 {4} | 80 | 32 {3} + 48 {4} | 82 | 40 {3} + 42 {4} | 194 | 80 {3} + 90 {4} + 24 {5} | ∞ | |
| Ячеек | 16 | 1 тетраэдр 4 треугольные призмы 6 треугольных призм 4 треугольные призмы 1 кубооктаэдр |
28 | 1 куб 6 квадратных призм 12 треугольных призм 8 треугольных пирамид 1 ромбокубооктаэдр |
28 | 1 октаэдр 8 треугольных призм 12 треугольных призм 6 квадратных пирамид 1 ромбокубооктаэдр |
64 | 1 додекаэдр 12 пятиугольных призм 30 треугольных призм 20 треугольных пирамид 1 ромбоикосододекаэдр |
∞ | 1 шестиугольная мозаика ∞ шестиугольных призм ∞ треугольных призм ∞ треугольных пирамид 1 ромботришестиугольная мозаика |
| Связанные однородные 4-мерные многогранники |
Рансинированный 5-ячейник |
Рансинированный тессеракт |
Рансинированный 24-ячейник |
Рансинированный 120-ячейник |
Рансинированные шестиугольные мозаичные соты | |||||
Примечания
- cupolas
- semicupolas
- Klitzing, 2000, pp. 139—181.
Литература
- N.W. Johnson. Convex Polyhedra with Regular Faces // Canad. J. Math. — 1966.. — Вып. 18. — С. 169–200.
- Dr. Richard Klitzing. Convex Segmentochora. — Symmetry: Culture and Science. — 2000. — Т. 11. — С. 139-181.
