Однородный звёздчатый многогранник

Однородный звёздчатый многогранник — самопересекающийся однородный многогранник. Эти многогранники называются также невыпуклыми многогранниками, подчёркивая самопересечение. Каждый многогранник может содержать грани в виде звёздчатых многоугольников или иметь звёздчатые вершинные фигуры, но может содержать и то, и другое.

Витрина с однородными многогранниками в Музее науки в Лондоне

Малый плосконосый икосоикосододекаэдр является однородным звёздчатым многогранником с вершинной фигурой 3⁵.⁵/₂

Полный набор 57 непризматических однородных звёздчатых многогранников включает 4 правильных, называемых телами Кеплера — Пуансо, 5 квазиправильных, и 48 полуправильных.

Существует также два бесконечных множества однородных звёздчатых призм и антипризм.

Так же, как (невырожденные) звёздчатые многоугольники (которые имеют плотность большую 1) соответствуют круговым многоугольникам с перекрывающимися частями, звёздчатые многогранники, которые не проходят через центр, имеют плотность, большую 1, и соответствуют сферическим многогранникам с перекрывающимися частями. Существует 48 таких непризматических однородных звёздчатых многогранников. Оставшиеся 9 непризматических однородных звёздчатых многогранников имеют грани, проходящие через центр, являются полумногогранниками и не соответствуют сферическим многогранникам, поскольку центр не может быть однозначно спроецирован на сферу.

Невыпуклые формы конструируются из треугольников Шварца.

Все треугольники, перечисленные ниже, сгруппированы по их группам симметрии, а внутри сгруппированы по расположению вершин.

Правильные многогранники помечены их символами Шлефли. Другие, неправильные однородные многогранники снабжены их вершинной конфигурацией или их номером однородного многогранника (Uniform polyhedron index, U(1-80)).

Примечание: Для невыпуклых форм ниже приводится дополнительное описание Неоднородный, когда выпуклая оболочка набора вершин имеет ту же топологию, но имеет неправильные грани. Например, неоднородное скашивание (удаление рёбер) может дать прямоугольники на местах удалённых рёбер, а не квадраты.

Диэдральная симметрия

См. Призматический однородный многогранник.

Тетраэдральная симметрия

Треугольники (3 3 2) на сфере

Существует один невыпуклый вид, тетрагемигексаэдр, который имеет тетраэдральную симметрию (с фундаментальной областью треугольник Мёбиуса (3 3 2)).

Существует два треугольника Шварца, из которых образуются уникальные невыпуклые однородные многогранники — прямоугольный треугольник (3/2 3 2) и один треугольник общего вида (3/2 3 3). Треугольник (3/2 3 3) генерирует октагемиоктаэдр, который приведён ниже в разделе октаэдральной симметрии.

Расположение вершин (Выпуклая оболочка)	Невыпуклые виды
Тетраэдр
Спрямлённый тетраэдр Октаэдр	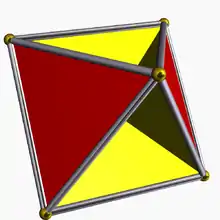(4.3/2.4.3) 3/2 3 \| 2
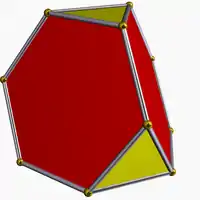Усечённый тетраэдр
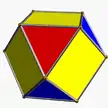Скошенный тетраэдр (Кубооктаэдр)
Всеусечённый тетраэдр (Усечённый октаэдр)
Плосконосый тетраэдр (Икосаэдр)

Октаэдральная симметрия

Треугольники (4 3 2) на сфере

Существует 8 выпуклых форм и 10 невыпуклых с октаэдральной симметрией (с фундаментальной областью треугольник Мёбиуса (4 3 2)).

Существует четыре треугольника Шварца, которые образуют невыпуклые формы, два прямоугольных, (3/2 4 2) и (4/3 3 2), и два общего вида, (4/3 4 3) и (3/2 4 4).

Расположение вершин (Выпуклая оболочка)	Невыпуклые виды
Куб
Октаэдр
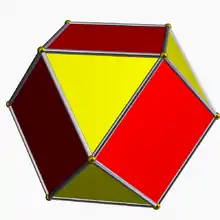Кубооктаэдр	(6.4/3.6.4) 4/3 4 \| 3	(6.3/2.6.3) 3/2 3 \| 3
Усечённый куб	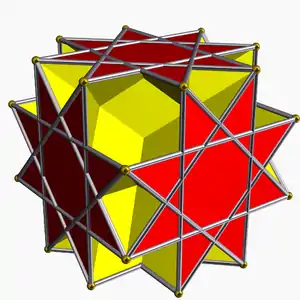4.8/3.4/3.8/5) 2 4/3 (3/2 4/2) \|	(8/3.3.8/3.4) 3 4 \| 4/3	(4.3/2.4.4) 3/2 4 \| 2
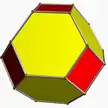Усечённый октаэдр
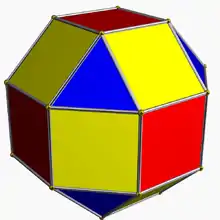Ромбокубооктаэдр	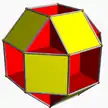(4.8.4/3.8) 2 4 (3/2 4/2) 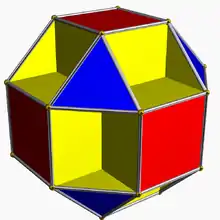\|	(8.3/2.8.4) 3/2 4 \| 4	(8/3.8/3.3) 2 3 \| 4/3
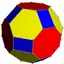Неоднородный Усечённый кубооктаэдр	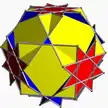(4.6.8/3) 2 3 4/3 \|
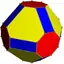Неоднородный Усечённый кубооктаэдр	(8/3.6.8) 3 4 4/3 \|
Плосконосый куб

Икосаэдральная симметрия

Треугольники (5 3 2) на сфере

Имеется 8 выпуклых форми и 46 невыпуклых с икосаэдральной симметрией (с фундаментальной областью треугольник Мёбиуса (5 3 2)). (или 47 невыпуклых форм, если включать фигуру Скиллинга). Некоторые невыпуклые плосконосые виды имеют зеркальную вершинную симметрию.

Расположение вершин (Выпуклая оболочка)	Невыпуклые виды
Икосаэдр	{5,5/2}	{5/2,5}	{3,5/2}
Неоднородный Усечённый икосаэдр 2 5 \|3	U37 2 5/2 \| 5	U61 5/2 3 \| 5/3	U67 5/3 3 \| 2	U73 2 5/3 (3/2 5/4) \|
Неоднородный Усечённый икосаэдр 2 5 \|3	U38 5/2 5 \| 2	U44 5/3 5 \| 3	U56 2 3 (5/4 5/2) \|
Неоднородный Усечённый икосаэдр 2 5 \|3	U32 \| 5/2 3 3
Икосододекаэдр 2 \| 3 5	U49 3/2 3 \| 5	U51 5/4 5 \| 5	U54 2 \| 3 5/2	U70 5/3 5/2 \| 5/3	U71 3 3 \| 5/3	U36 2 \| 5 5/2	U62 5/3 5/2 \| 3	U65 5/4 5 \| 3
Усечённый додекаэдр 2 3 \| 5	U42	U48	U63
Неоднородный усечённый додекаэдр	U72
Додекаэдр	{5/2,3}	U30	U41	U47
Ромбоикосододекаэдр	U33	U39	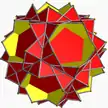U58
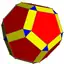Додекаэдр со снятыми кромками	U55
Неоднородный Ромбоикосододекаэдр	U31	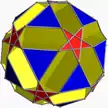U43	U50	U66
Неоднородный ромбоикосододекаэдр	U75	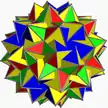U64	Тело Скиллинга (см. ниже)
Неоднородный Ромбоусечённый икосододекаэдр	U45
Неоднородный Ромбоусечённый икосододекаэдр	U59
Неоднородный Ромбоусечённый икосододекаэдр	U68
Неоднородный Плосконосый додекаэдр	U40	U46	U57	U69	U60	U74

Тело Скиллинга

Ещё одним невыпуклым многогранником является большой биплосконосый биромбододекаэдр, известный также как тело Скиллинга, которое вершинно однородно, но имеет разделяемые общие для граней пары рёбер, так что четыре грани имеют одно общее ребро. Иногда его причисляют к однородным многогранникам, но не всегда. Тело имеет симметрию I_h.

Вырожденные случаи

Коксетер с помощью построения Витхоффа определил некоторое число вырожденных звёздчатых многогранников, которые имеют перекрывающиеся рёбра или вершины. Эти вырожденные формы включают:

Малый составной икосододекаэдр
Большой составной икосододекаэдр
Малый составной ромбоикосододекаэдр
Составной ромбододекододекаэдр
Большой составной ромбоикосододекаэдр

См. также

Примечания

Литература

H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller. Uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, вып. 916. — С. 401–450. — ISSN 0080-4614. — doi:10.1098/rsta.1954.0003. — .
М. Веннинджер. Модели многогранников. — «Мир», 1974.
M. Brückner. Vielecke und vielflache. Theorie und geschichte. — Leipzig, Germany: Teubner, 1900.
С.П. Сопов. Доказательство полноты перечня элементарных однородных многогранников // Украинский геометрический сборник. — 1970. — Вып. 8. — С. 139–156.
J. Skilling. The complete set of uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — 1975. — Т. 278. — С. 111–135. — ISSN 0080-4614. — doi:10.1098/rsta.1975.0022. — .
Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El, Kaleido software, Images, dual images
R. E. Mäder. Uniform Polyhedra // Mathematica. — 1993. — Вып. 3. — С. 48-57.
Peter W. Messer. Closed-Form Expressions for Uniform Polyhedra and Their Duals // Discrete & Computational Geometry. — 2002. — Вып. 27. — С. 353-375.
Richard Klitzing, 3D, uniform polyhedra

Ссылки

Weisstein, Eric W. Uniform Polyhedron (англ.) на сайте Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.