Список однородных многогранников по порождающим треугольникам Шварца

Существует много связей между однородными многогранниками. Построение Витхоффа способно построить почти все однородные многогранники из треугольников Шварца. Числа, которые могут быть использованы для сторон недиэдрического треугольника Шварца, которые не обязательно приводят только к вырожденным многогранникам, равны 2, 3, 3/2, 4, 4/3, 5, 5/2, 5/3 и 5/4 (но числа с числителями 4 и 5 не могут встречаться вместе). Число 4/2 тоже можно использовать, но оно приводит к вырожденным однородным многогранникам, поскольку 4 и 2 имеют общий делитель. Существует 44 таких треугольников Шварца (5 с тетраэдральной симметрией, 7 с октаэдральной симметрией и 32 с икосаэдральной симметрией), которые, вместе с бесконечным семейством диэдрических треугольников Шварца, могут образовать почти все невырожденные однородные многогранники. Многие вырожденные однородные многогранники с полностью совпадающими вершинами, рёбрами или гранями могут быть также сгенерированы с помощью построения Витхоффа, и те, которые возникают из треугольников Шварца, не использующих 4/2, также включены в таблицы ниже вместе с их невырожденными аналогами.

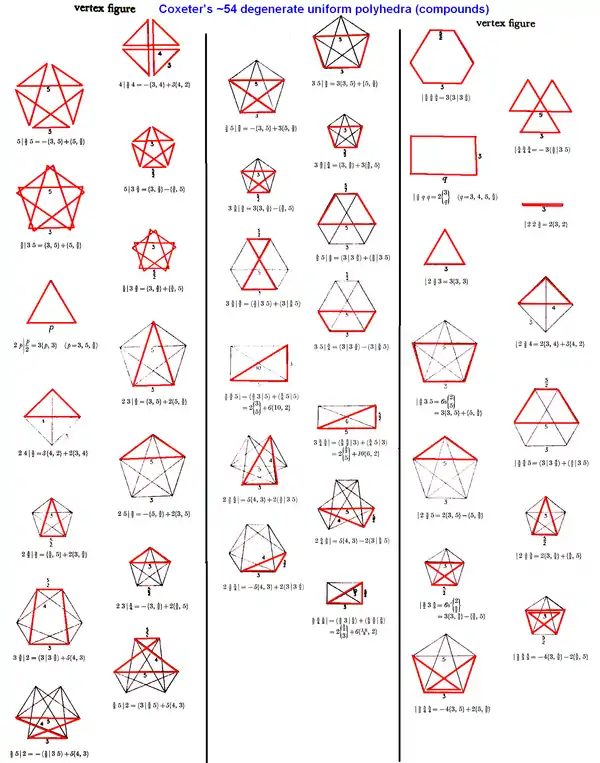
Список Коксетера вырожденных витхоффовых однородных многогранников с указанием символов Витхоффа, вершинных фигур и символов Шлефли. Все однородные многогранники и все вырожденные витхоффовы однородные многогранники перечислены в этой статье.

Существует несколько невитхоффовых однородных многогранника, которые треугольники Шварца не могут сгенерировать. Однако большинство из них может быть получено с помощью построения Витхоффа как двойное покрытие (невитхоффов многогранник покрывается дважды) или с несколькими дополнительными гранями (см. Всеусечённый многогранник). Такие многогранники помечены в списке звёздочкой. Только для двух однородных многогранников построение Витхоффа не работает — это Большой биромбоикосододекаэдр и Большой биплосконосый биромбобидодекаэдр.

Каждая мозаика треугольников Шварца на сфере может покрыть сферу только раз, либо, вместо этого, обойти сферу кратное число раз, пересекая себя в процессе покрытия. Число раз, которые мозаика оборачивает сферу, является плотностью мозаики и обозначается μ.

Для экономии места в статье используются короткие имена многогранников, данные Джонатаном Бауэрсом (Jonathan Bowers), и известные как сокращения (акронимы) Бауэрса. Номер Маедера (система «Mathematic»[1][2]) также дан. За исключением диэдрических треугольников Шварца, треугольники Шварца упорядочены по их плотности.

Треугольники Мёбиуса и Шварца

Согласно книге Коксетера (Коксетер, «Uniform polyhedra»[3]), существует 4 сферических треугольника с углами π/p, π/q, π/r, где (p q r) — целые числа:

  1. (2 2 r) — Диэдральный
  2. (2 3 3) — Тетраэдраьный
  3. (2 3 4) — Октаэдральный
  4. (2 3 5) — Икосаэдральный

Они называются треугольниками Мёбиуса.

В треугольнике Шварца кроме этих троек допускаются (p q r) с рациональными числами.

Плотность (μ) Треугольники
1(2 3 3)(2 3 4)(2 3 5)
d(2 2 n/d)
2(3/2 3 3)(3/2 4 4)(3/2 5 5)(5/2 3 3)
3(2 3/2 3)(2 5/2 5)
4(3 4/3 4)(3 5/3 5)
5(2 3/2 3/2)(2 3/2 4)
6(3/2 3/2 3/2)(5/2 5/2 5/2)(3/2 3 5)(5/4 5 5)
7(2 3 4/3)(2 3 5/2)
8(3/2 5/2 5)
9(2 5/3 5)
10(3 5/3 5/2)(3 5/4 5)
11(2 3/2 4/3)(2 3/2 5)
13(2 3 5/3)
14(3/2 4/3 4/3)(3/2 5/2 5/2)(3 3 5/4)
16(3 5/4 5/2)
17(2 3/2 5/2)
18(3/2 3 5/3)(5/3 5/3 5/2)
19(2 3 5/4)
21(2 5/4 5/2)
22(3/2 3/2 5/2)
23(2 3/2 5/3)
26(3/2 5/3 5/3)
27(2 5/4 5/3)
29(2 3/2 5/4)
32(3/2 5/4 5/3)
34(3/2 3/2 5/4)
38(3/2 5/4 5/4)
42(5/4 5/4 5/4)

Сводная таблица

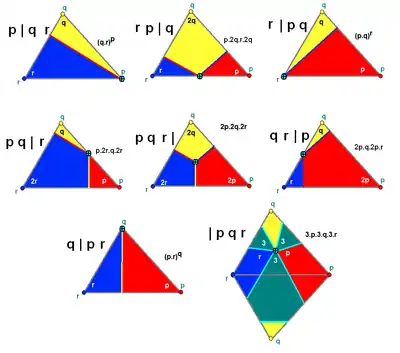
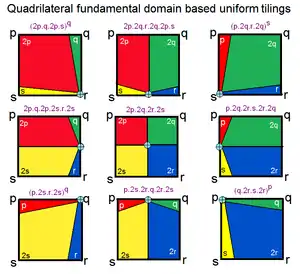
Существует семь генерирующих точек в каждом наборе p, q, r (и несколько специальных случаев):

Общий случай Прямоугольный треугольник (r=2)
Описание Символ
Витхоффа		 Конфигурация
вершины		 Диаграмма
Коксетера
 Символ
Витхоффа		 Конфигурация
вершины		 Символ
Шлефли		 Диаграмма
Коксетера
правильный и
квазиправильный		 q | p r (p.r)q q | p 2 pq {p,q}
p | q r (q.r)p p | q 2 qp {q,p}
r | p q (q.p)r 2 | p q (q.p)² t1{p,q}
усечённый и
растянутый		 q r | p q.2p.r.2p q 2 | p q.2p.2p t0,1{p,q}
p r | q p.2q.r.2q p 2 | q p.2q.2q t0,1{q,p}
p q | r 2r.q.2r.p p q | 2 4.q.4.p t0,2{p,q}
с чётным
числом
граней		 p q r | 2r.2q.2p p q 2 | 4.2q.2p t0,1,2{p,q}
p q r
s |		 2p.2q.-2p.-2q - p 2 r
s |		 2p.4.-2p.4/3 -
плосконосый | p q r 3.r.3.q.3.p | p q 2 3.3.q.3.p sr{p,q}
| p q r s (4.p.4.q.4.r.4.s)/2 - - - -

Существует четыре специальных случая:

  • p q r
    s     |     — Смесь p q r | и p q s |. Оба символа p q r | и p q s | образуют общий базовый многогранник с некоторыми дополнительными гранями. Запись p q r
    s     |     тогда представляет базовый многогранник, сделанный из общих граней p q r | и p q s |.
  • | p q r — Плосконосые формы (альтернированные).
  • | p q r s — Единственная плосконосая форма для U75, который не получается из построения Витхоффа с использованием треугольной фундаментальной области. В этот символ Витхоффа входят четыре числа, поскольку имеет четырёхугольную сферическую фундаментальную область.
  • | (p) q (r) s — Единственная плосконосая форма для фигуры Скиллинга, которую нельзя получить построением Витхоффа.

Эта таблица преобразования символа Витхоффа в конфигурацию вершины не работает для некоторых исключительных однородных многогранников. Единственными невырожденными такими случаями являются большой усечённый кубооктаэдр (2 3 4/3 |), усечённый додекододекаэдр (2 5/3 5 |), Большой икосаэдр (| 2 3/2 3/2), большой вывернутый обратноплосконосый икосододекаэдр (| 2 3/2 5/3) и малый плосконосый икосоикосододекаэдр (| 3/2 3/2 5/2). В этих случаях вершинная фигура является крайне деформированной для того, чтобы получить однородность с плоскими гранями — в первых двух случаях это тупоугольный треугольник, а не остроугольный, а в последних трёх случаях это пентаграмма или гексаграмма вместо пятиугольника или шестиугольника, и они оборачиваются вокруг центра дважды. Это приводит к тому, что часть граней проходят сквозь многогранник и выходят с другой стороны многогранника. По этой же причине плотность многогранника не совпадает с плотностью треугольника Шварца, из которого они получены, и равны 1, 3, 7, 37 и 38 соответственно.

Диэдральные (Призматические)

В диэдральных треугольниках Шварца два числа равны 2, а третье может быть произвольным рациональным числом, строго большим 1.

  1. (2 2 n/d) – вырожденный, если НОД(n, d) > 1.

Много многогранников с диэдральной симметрией имеют двуугольные грани, что делает их вырожденными многогранниками (то есть диэдрами и осоэдрами). Столбцы таблицы, содержащие только вырожденные многогранники не включены — специальные вырожденные случаи (только для треугольников Шварца (2 2 2)) помечены большим крестом. Скрещенные антипризмы с третьим значением {p}, где p < 3/2 существовать не могут, поскольку их вершинные фигуры тогда нарушили бы неравенство треугольника. Эти невозможные фигуры также отмечены большим крестом. 3/2-скрещенная антипризма является вырожденной, поскольку в евклидовом пространстве она плоская, а потому тоже помечена большим крестом. Треугольники Шварца (2 2 n/d) перечислены здесь только для случаев НОД (n, d) = 1, в противном случае все полученные многогранники будут вырожденными.

Список даёт все возможные случаи для n ≤ 6.

(p q r) q r | p
q.2p.r.2p		 p r | q
p.2q.r.2q		 p q r |
2r.2q.2p		 | p q r
3.r.3.q.3.p
(2 2 2)
(μ=1)
X
X
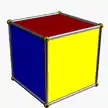4.4.4
cube
4-p
3.3.3
tet
2-ap
(2 2 3)
(μ=1)
4.3.4
trip
3-p
4.3.4
trip
3-p
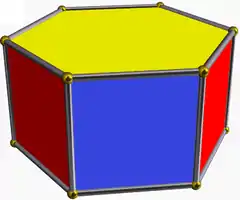6.4.4
hip
6-p
3.3.3.3
oct
3-ap
(2 2 3/2)
(μ=2)
4.3.4
trip
3-p
4.3.4
trip
3-p
6/2.4.4
2trip
6/2-p
X
(2 2 4)
(μ=1)
4.4.4
cube
4-p
4.4.4
cube
4-p
8.4.4
op
8-p
3.4.3.3
squap
4-ap
(2 2 4/3)
(μ=3)
4.4.4
cube
4-p
4.4.4
cube
4-p
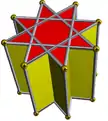8/3.4.4
stop
8/3-p
X
(2 2 5)
(μ=1)
4.5.4
pip
5-p
4.5.4
pip
5-p
10.4.4
dip
10-p
3.5.3.3
pap
5-ap
(2 2 5/2)
(μ=2)
4.5/2.4
stip
5/2-p
4.5/2.4
stip
5/2-p
10/2.4.4
2pip
10/2-p
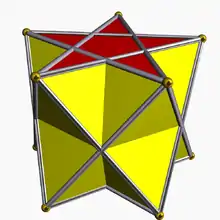3.5/2.3.3
stap
5/2-ap
(2 2 5/3)
(μ=3)
4.5/2.4
stip
5/2-p
4.5/2.4
stip
5/2-p
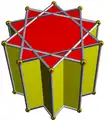10/3.4.4
stiddip
10/3-p
3.5/3.3.3
starp
5/3-ap
(2 2 5/4)
(μ=4)
4.5.4
pip
5-p
4.5.4
pip
5-p
10/4.4.4
–
10/4-p
X
(2 2 6)
(μ=1)
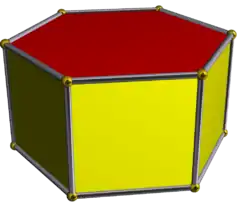4.6.4
hip
6-p
4.6.4
hip
6-p
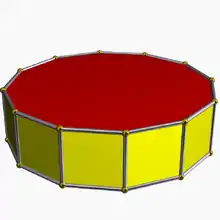12.4.4
twip
12-p
3.6.3.3
hap
6-ap
(2 2 6/5)
(μ=5)
4.6.4
hip
6-p
4.6.4
hip
6-p
12/5.4.4
stwip
12/5-p
X
(2 2 n)
(μ=1)		 4.n.4
n-p		 4.n.4
n-p		 2n.4.4
2n-p		 3.n.3.3
n-ap
(2 2 n/d)
(μ=d)		 4.n/d.4
n/d-p		 4.n/d.4
n/d-p		 2n/d.4.4
2n/d-p		 3.n/d.3.3
n/d-ap

Тетраэдральные

В тетраэдральных треугольниках Шварца максимальный числитель не должен превосходить 3.

  1. (3 3 2)
  2. (3 3 3/2)
  3. (3 2 3/2)
  4. (2 3/2 3/2)
  5. (3/2 3/2 3/2)
# (p q r) q | p r
(p.r)q		 p | q r
(q.r)p		 r | p q
(q.p)r		 q r | p
q.2p.r.2p		 p r | q
p.q.r.2q		 p q | r
2r.q.2r.p		 p q r |
2r.2q.2p		 | p q r
3.r.3.q.3.p
1 (3 3 2)
(µ=1)
3.3.3
tet
U1
3.3.3
tet
U1
3.3.3.3
oct
U5
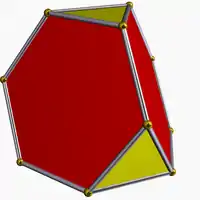3.6.6
tut
U2
3.6.6
tut
U2
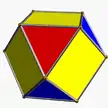4.3.4.3
co
U7
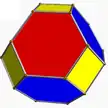4.6.6
toe
U8
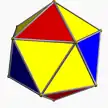3.3.3.3.3
ike
U22
2 (3 3 3/2)
(µ=2)
(3.3.3.3.3.3)/2
2tet
–
(3.3.3.3.3.3)/2
2tet
–
(3.3.3.3.3.3)/2
2tet
–
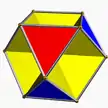3.6.3/2.6
oho
U3
3.6.3/2.6
oho
U3
2(6/2.3.6/2.3)
2oct
–
2(6/2.6.6)
2tut
–
2(3.3/2.3.3.3.3)
2oct+8{3}
–
3 (3 2 3/2)
(µ=3)
3.3.3.3
oct
U5
3.3.3
tet
U1
3.3.3
tet
U1
3.6.6
tut
U2
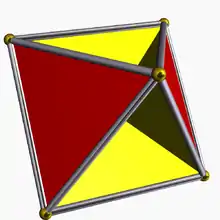2(3/2.4.3.4)
2thah
U4*
3(3.6/2.6/2)
3tet
–
2(6/2.4.6)
cho+4{6/2}

U15*
?
4 (2 3/2 3/2)
(µ=5)
3.3.3
tet
U1
3.3.3.3
oct
U5
3.3.3
tet
U1
3.4.3.4
co
U7
3(6/2.3.6/2)
3tet
–
3(6/2.3.6/2)
3tet
–
4(6/2.6/2.4)
2oct+6{4}
–
(3.3.3.3.3)/2
gike
U53
5 (3/2 3/2 3/2)
(µ=6)
(3.3.3.3.3.3)/2
2tet
–
(3.3.3.3.3.3)/2
2tet
–
(3.3.3.3.3.3)/2
2tet
–
2(6/2.3.6/2.3)
2oct
–
2(6/2.3.6/2.3)
2oct
–
2(6/2.3.6/2.3)
2oct
–
6(6/2.6/2.6/2)
6tet
–
?

Октаэдральные

В октаэдральных треугольниках Шварца максимальным разрешённым числителем является 4. Существуют также октаэдральные треугольники с 4/2, но они дают только вырожденные однородные многогранники, поскольку 4 и 2 не взаимно просты.

  1. (4 3 2)
  2. (4 4 3/2)
  3. (4 3 4/3)
  4. (4 2 3/2)
  5. (3 2 4/3)
  6. (2 3/2 4/3)
  7. (3/2 4/3 4/3)
# (p q r) q | p r
(p.r)q		 p | q r
(q.r)p		 r | p q
(q.p)r		 q r | p
q.2p.r.2p		 p r | q
p.2q.r.2q		 p q | r
2r.q.2r.p		 p q r |
2r.2q.2p		 | p q r
3.r.3.q.3.p
1 (4 3 2)
(µ=1)
4.4.4
cube
U6
3.3.3.3
oct
U5
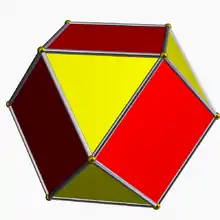3.4.3.4
co
U7
3.8.8
tic
U9
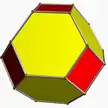4.6.6
toe
U8
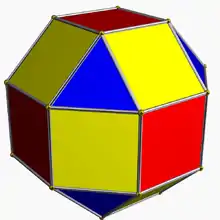4.3.4.4
sirco
U10
4.6.8
girco
U11
3.3.3.3.4
snic
U12
2 (4 4 3/2)
(µ=2)
(3/2.4)4
oct+6{4}
–
(3/2.4)4
oct+6{4}
–
(4.4.4.4.4.4)/2
2cube
–
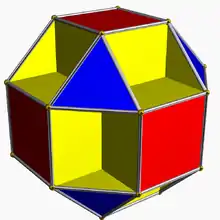3/2.8.4.8
socco
U13
3/2.8.4.8
socco
U13
2(6/2.4.6/2.4)
2co
–
2(6/2.8.8)
2tic
–
?
3 (4 3 4/3)
(µ=4)
(4.4.4.4.4.4)/2
2cube
–
(3/2.4)4
oct+6{4}
–
(3/2.4)4
oct+6{4}
–
3/2.8.4.8
socco
U13
2(4/3.6.4.6)
2cho
U15*
3.8/3.4.8/3
gocco
U14
6.8.8/3
cotco
U16
?
4 (4 2 3/2)
(µ=5)
3.4.3.4
co
U7
3.3.3.3
oct
U5
4.4.4
cube
U6
3.8.8
tic
U9
4.4.3/2.4
querco
U17
4(4.6/2.6/2)
2oct+6{4}
–
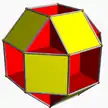2(4.6/2.8)
sroh+8{6/2}
U18*
?
5 (3 2 4/3)
(µ=7)
3.4.3.4
co
U7
4.4.4
cube
U6
3.3.3.3
oct
U5
4.6.6
toe
U8
4.4.3/2.4
querco
U17
3.8/3.8/3
quith
U19
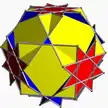4.6/5.8/3
quitco
U20
?
6 (2 3/2 4/3)
(µ=11)
4.4.4
cube
U6
3.4.3.4
co
U7
3.3.3.3
oct
U5
4.3.4.4
sirco
U10
4(4.6/2.6/2)
2oct+6{4}
–
3.8/3.8/3
quith
U19
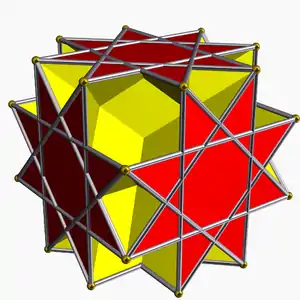2(4.6/2.8/3)
groh+8{6/2}
U21*
?
7 (3/2 4/3 4/3)
(µ=14)
(3/2.4)4 = (3.4)4/3
oct+6{4}
–
(4.4.4.4.4.4)/2
2cube
–
(3/2.4)4 = (3.4)4/3
oct+6{4}
–
2(6/2.4.6/2.4)
2co
–
3.8/3.4.8/3
gocco
U14
3.8/3.4.8/3
gocco
U14
2(6/2.8/3.8/3)
2quith
–
?

Икосаэдральные

В икосаэдральных треугольниках Шварца максимальным разрешённым числителем может быть 5. Кроме того, числитель 4 не может быть использован во всех икосаэдральных треугольниках Шварца, хотя числители 2 и 3 разрешены. (Если бы 4 и 5 могли появляться одновременно в некоторых треугольниках Шварца, они должны были бы появиться и в некоторых треугольниках Мёбиуса, но это невозможно, так как (2 4 5) является гиперболическим треугольником, а не сферическим.)

  1. (5 3 2)
  2. (3 3 5/2)
  3. (5 5 3/2)
  4. (5 5/2 2)
  5. (5 3 5/3)
  6. (5/2 5/2 5/2)
  7. (5 3 3/2)
  8. (5 5 5/4)
  9. (3 5/2 2)
  10. (5 5/2 3/2)
  11. (5 2 5/3)
  12. (3 5/2 5/3)
  13. (5 3 5/4)
  14. (5 2 3/2)
  15. (3 2 5/3)
  16. (5/2 5/2 3/2)
  17. (3 3 5/4)
  18. (3 5/2 5/4)
  19. (5/2 2 3/2)
  20. (5/2 5/3 5/3)
  21. (3 5/3 3/2)
  22. (3 2 5/4)
  23. (5/2 2 5/4)
  24. (5/2 3/2 3/2)
  25. (2 5/3 3/2)
  26. (5/3 5/3 3/2)
  27. (2 5/3 5/4)
  28. (2 3/2 5/4)
  29. (5/3 3/2 5/4)
  30. (3/2 3/2 5/4)
  31. (3/2 5/4 5/4)
  32. (5/4 5/4 5/4)
# (p q r) q | p r
(p.r)q		 p | q r
(q.r)p		 r | p q
(q.p)r		 q r | p
q.2p.r.2p		 p r | q
p.2q.r.2q		 p q | r
2r.q.2r.p		 p q r |
2r.2q.2p		 | p q r
3.r.3.q.3.p
1 (5 3 2)
(µ=1)
5.5.5
doe
U23
3.3.3.3.3
ike
U22
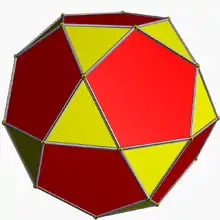3.5.3.5
id
U24
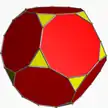3.10.10
tid
U26
5.6.6
ti
U25
4.3.4.5
srid
U27
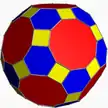4.6.10
grid
U28
3.3.3.3.5
snid
U29
2 (3 3 5/2)
(µ=2)
3.5/2.3.5/2.3.5/2
sidtid
U30
3.5/2.3.5/2.3.5/2
sidtid
U30
(310)/2
2ike
–
3.6.5/2.6
siid
U31
3.6.5/2.6
siid
U31
2(10/2.3.10/2.3)
2id
–
2(10/2.6.6)
2ti
–
3.5/2.3.3.3.3
seside

U32

3 (5 5 3/2)
(µ=2)
(5.3/2)5
cid
–
(5.3/2)5
cid
–
(5.5.5.5.5.5)/2
2doe
–
5.10.3/2.10
saddid
U33
5.10.3/2.10
saddid
U33
2(6/2.5.6/2.5)
2id
–
2(6/2.10.10)
2tid
–
2(3.3/2.3.5.3.5)
2id+40{3}
–
4 (5 5/2 2)
(µ=3)
(5.5.5.5.5)/2
gad
U35
5/2.5/2.5/2.5/2.5/2
sissid
U34
5/2.5.5/2.5
did
U36
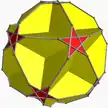5/2.10.10
tigid
U37
5.10/2.10/2
3doe
–
4.5/2.4.5
raded
U38
2(4.10/2.10)
sird+12{10/2}
U39*
3.3.5/2.3.5
siddid
U40
5 (5 3 5/3)
(µ=4)
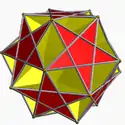5.5/3.5.5/3.5.5/3
ditdid
U41
(3.5/3)5
gacid
–
(3.5)5/3
cid
–
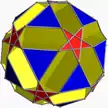3.10.5/3.10
sidditdid
U43
5.6.5/3.6
ided
U44
10/3.3.10/3.5
gidditdid
U42
10/3.6.10
idtid
U45
3.5/3.3.3.3.5
sided
U46
6 (5/2 5/2 5/2)
(µ=6)
(5/2)10/2
2sissid
–
(5/2)10/2
2sissid
–
(5/2)10/2
2sissid
–
2(5/2.10/2)2
2did
–
2(5/2.10/2)2
2did
–
2(5/2.10/2)2
2did
–
6(10/2.10/2.10/2)
6doe
–
3(3.5/2.3.5/2.3.5/2)
3sidtid
–
7 (5 3 3/2)
(µ=6)
(3.5.3.5.3.5)/2
gidtid
U47
(310)/4
2gike
–
(3.5.3.5.3.5)/2
gidtid
U47
2(3.10.3/2.10)
2seihid
U49*
5.6.3/2.6
giid
U48
5(6/2.3.6/2.5)
3ike+gad
–
2(6.6/2.10)
siddy+20{6/2}
U50*
5(3.3.3.3.3.5)/2
5ike+gad
–
8 (5 5 5/4)
(µ=6)
(510)/4
2gad
–
(510)/4
2gad
–
(510)/4
2gad
–
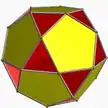2(5.10.5/4.10)
2sidhid
U51*
2(5.10.5/4.10)
2sidhid
U51*
10/4.5.10/4.5
2did
–
2(10/4.10.10)
2tigid
–
3(3.5.3.5.3.5)
3cid
–
9 (3 5/2 2)
(µ=7)
(3.3.3.3.3)/2
gike
U53
5/2.5/2.5/2
gissid
U52
5/2.3.5/2.3
gid
U54
5/2.6.6
tiggy
U55
3.10/2.10/2
2gad+ike
–
3(4.5/2.4.3)
sicdatrid
–
4.10/2.6
ri+12{10/2}
U56*
3.3.5/2.3.3
gosid
U57
10 (5 5/2 3/2)
(µ=8)
(5.3/2)5
cid
–
(5/3.3)5
gacid
–
5.5/3.5.5/3.5.5/3
ditdid
U41
5/3.10.3.10
sidditdid
U43
5(5.10/2.3.10/2)
ike+3gad
–
3(6/2.5/2.6/2.5)
sidtid+gidtid
–
4(6/2.10/2.10)
id+seihid+sidhid
–
?
11 (5 2 5/3)
(µ=9)
5.5/2.5.5/2
did
U36
5/2.5/2.5/2.5/2.5/2
sissid
U34
(5.5.5.5.5)/2
gad
U35
5/2.10.10
tigid
U37
3(5.4.5/3.4)
cadditradid
–
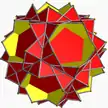10/3.5.5
quit sissid
U58
10/3.4.10/9
quitdid
U59
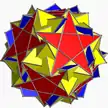3.5/3.3.3.5
isdid
U60
12 (3 5/2 5/3)
(µ=10)
(3.5/3)5
gacid
–
(5/2)6/2
2gissid
–
(5/2.3)5/3
gacid
–
2(5/2.6.5/3.6)
2sidhei
U62*
3(3.10/2.5/3.10/2)
ditdid+gidtid
–
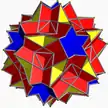10/3.5/2.10/3.3
gaddid
U61
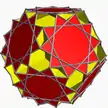10/3.10/2.6
giddy+12{10/2}
U63*
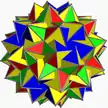3.5/3.3.5/2.3.3
gisdid
U64
13 (5 3 5/4)
(µ=10)
(5.5.5.5.5.5)/2
2doe
–
(3/2.5)5
cid
–
(3.5)5/3
cid
–
3/2.10.5.10
saddid
U33
2(5.6.5/4.6)
2gidhei
U65*
3(10/4.3.10/4.5)
sidtid+ditdid
–
2(10/4.6.10)
siddy+12{10/4}
U50*
?
14 (5 2 3/2)
(µ=11)
5.3.5.3
id
U24
3.3.3.3.3
ike
U22
5.5.5
doe
U23
3.10.10
tid
U26
3(5/4.4.3/2.4)
gicdatrid
–
5(5.6/2.6/2)
2ike+gad
–
2(6/2.4.10)
sird+20{6/2}
U39*
5(3.3.3.5.3)/2
4ike+gad
–
15 (3 2 5/3)
(µ=13)
3.5/2.3.5/2
gid
U54
5/2.5/2.5/2
gissid
U52
(3.3.3.3.3)/2
gike
U53
5/2.6.6
tiggy
U55
3.4.5/3.4
qrid
U67
10/3.10/3.3
quit gissid
U66
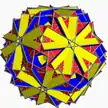10/3.4.6
gaquatid
U68
3.5/3.3.3.3
gisid
U69
16 (5/2 5/2 3/2)
(µ=14)
(5/3.3)5
gacid
–
(5/3.3)5
gacid
–
(5/2)6/2
2gissid
–
3(5/3.10/2.3.10/2)
ditdid+gidtid
–
3(5/3.10/2.3.10/2)
ditdid+gidtid
–
2(6/2.5/2.6/2.5/2)
2gid
–
10(6/2.10/2.10/2)
2ike+4gad
–
?
17 (3 3 5/4)
(µ=14)
(3.5.3.5.3.5)/2
gidtid
U47
(3.5.3.5.3.5)/2
gidtid
U47
(3)10/4
2gike
–
3/2.6.5.6
giid
U48
3/2.6.5.6
giid
U48
2(10/4.3.10/4.3)
2gid
–
2(10/4.6.6)
2tiggy
–
?
18 (3 5/2 5/4)
(µ=16)
(3/2.5)5
cid
–
5/3.5.5/3.5.5/3.5
ditdid
U41
(5/2.3)5/3
gacid
–
5/3.6.5.6
ided
U44
5(3/2.10/2.5.10/2)
ike+3gad
–
5(10/4.5/2.10/4.3)
3sissid+gike
–
4(10/4.10/2.6)
did+sidhei+gidhei
–
?
19 (5/2 2 3/2)
(µ=17)
3.5/2.3.5/2
gid
U54
(3.3.3.3.3)/2
gike
U53
5/2.5/2.5/2
gissid
U52
5(10/2.3.10/2)
2gad+ike
–
5/3.4.3.4
qrid
U67
5(6/2.6/2.5/2)
2gike+sissid
–
6(6/2.4.10/2)
2gidtid+rhom
–
?
20 (5/2 5/3 5/3)
(µ=18)
(5/2)10/2
2sissid
–
(5/2)10/2
2sissid
–
(5/2)10/2
2sissid
–
2(5/2.10/2)2
2did
–
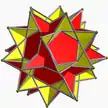2(5/2.10/3.5/3.10/3)
2gidhid
U70*
2(5/2.10/3.5/3.10/3)
2gidhid
U70*
2(10/3.10/3.10/2)
2quitsissid
–
?
21 (3 5/3 3/2)
(µ=18)
(310)/2
2ike
–
5/2.3.5/2.3.5/2.3
sidtid
U30
5/2.3.5/2.3.5/2.3
sidtid
U30
5/2.6.3.6
siid
U31
2(3.10/3.3/2.10/3)
geihid
U71*
5(6/2.5/3.6/2.3)
sissid+3gike
–
2(6/2.10/3.6)
giddy+20{6/2}
U63*
?
22 (3 2 5/4)
(µ=19)
3.5.3.5
id
U24
5.5.5
doe
U23
3.3.3.3.3
ike
U22
5.6.6
ti
U25
3(3/2.4.5/4.4)
gicdatrid
–
5(10/4.10/4.3)
2sissid+gike
–
2(10/4.4.6)
ri+12{10/4}
U56*
?
23 (5/2 2 5/4)
(µ=21)
5/2.5.5/2.5
did
U36
(5.5.5.5.5)/2
gad
U35
5/2.5/2.5/2.5/2.5/2
sissid
U34
3(10/2.5.10/2)
3doe
–
3(5/3.4.5.4)
cadditradid
–
3(10/4.5/2.10/4)
3gissid
–
6(10/4.4.10/2)
2ditdid+rhom
–
?
24 (5/2 3/2 3/2)
(µ=22)
5/2.3.5/2.3.5/2.3
sidtid
U30
(310)/2
2ike
–
5/2.3.5/2.3.5/2.3
sidtid
U30
2(3.10/2.3.10/2)
2id
–
5(5/3.6/2.3.6/2)
sissid+3gike
–
5(5/3.6/2.3.6/2)
sissid+3gike
–
10(6/2.6/2.10/2)
4ike+2gad
–
(3.3.3.3.3.5/2)/2
sirsid
U72
25 (2 5/3 3/2)
(µ=23)
(3.3.3.3.3)/2
gike
U53
5/2.3.5/2.3
gid
U54
5/2.5/2.5/2
gissid
U52
3(5/2.4.3.4)
sicdatrid
–
10/3.3.10/3
quit gissid
U66
5(6/2.5/2.6/2)
2gike+sissid
–
2(6/2.10/3.4)
gird+20{6/2}
U73*
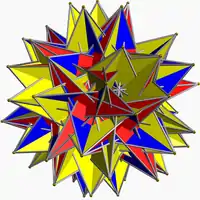(3.3.3.5/2.3)/2
girsid
U74
26 (5/3 5/3 3/2)
(µ=26)
(5/2.3)5/3
gacid
–
(5/2.3)5/3
gacid
–
(5/2)6/2
2gissid
–
5/2.10/3.3.10/3
gaddid
U61
5/2.10/3.3.10/3
gaddid
U61
2(6/2.5/2.6/2.5/2)
2gid
–
2(6/2.10/3.10/3)
2quitgissid
–
?
27 (2 5/3 5/4)
(µ=27)
(5.5.5.5.5)/2
gad
U35
5/2.5.5/2.5
did
U36
5/2.5/2.5/2.5/2.5/2
sissid
U34
5/2.4.5.4
raded
U38
10/3.5.10/3
quit sissid
U58
3(10/4.5/2.10/4)
3gissid
–
2(10/4.10/3.4)
gird+12{10/4}
U73*
?
28 (2 3/2 5/4)
(µ=29)
5.5.5
doe
U23
3.5.3.5
id
U24
3.3.3.3.3
ike
U22
3.4.5.4
srid
U27
2(6/2.5.6/2)
2ike+gad
–
5(10/4.3.10/4)
2sissid+gike
–
6(10/4.6/2.4/3)
2sidtid+rhom
–
?
29 (5/3 3/2 5/4)
(µ=32)
5/3.5.5/3.5.5/3.5
ditdid
U41
(3.5)5/3
cid
–
(3.5/2)5/3
gacid
–
3.10/3.5.10/3
gidditdid
U42
3(5/2.6/2.5.6/2)
sidtid+gidtid
–
5(10/4.3.10/4.5/2)
3sissid+gike
–
4(10/4.6/2.10/3)
gid+geihid+gidhid
–
?
30 (3/2 3/2 5/4)
(µ=34)
(3.5.3.5.3.5)/2
gidtid
U47
(3.5.3.5.3.5)/2
gidtid
U47
(3)10/4
2gike
–
5(3.6/2.5.6/2)
3ike+gad
–
5(3.6/2.5.6/2)
3ike+gad
–
2(10/4.3.10/4.3)
2gid
–
10(10/4.6/2.6/2)
2sissid+4gike
–
?
31 (3/2 5/4 5/4)
(µ=38)
(3.5)5/3
cid
–
(5.5.5.5.5.5)/2
2doe
–
(3.5)5/3
cid
–
2(5.6/2.5.6/2)
2id
–
3(3.10/4.5/4.10/4)
sidtid+ditdid
–
3(3.10/4.5/4.10/4)
sidtid+ditdid
–
10(10/4.10/4.6/2)
4sissid+2gike
–
5(3.3.3.5/4.3.5/4)
4ike+2gad
–
32 (5/4 5/4 5/4)
(µ=42)
(5)10/4
2gad
–
(5)10/4
2gad
–
(5)10/4
2gad
–
2(5.10/4.5.10/4)
2did
–
2(5.10/4.5.10/4)
2did
–
2(5.10/4.5.10/4)
2did
–
6(10/4.10/4.10/4)
2gissid
–
3(3/2.5.3/2.5.3/2.5)
3cid
–

Невитхоффовы

Геми-формы

Эти многогранники (полумногогранники) получаются как двойное покрытие с помощью построения Витхоффа. Если фигура, полученная построением Витхоффа, составлена из двух идентичных компонент, операция «геми» берёт только одну компоненту.


3/2.4.3.4
thah
U4
hemi(3 3/2 | 2)
4/3.6.4.6
cho
U15
hemi(4 4/3 | 3)
5/4.10.5.10
sidhid
U51
hemi(5 5/4 | 5)
5/2.6.5/3.6
sidhei
U62
hemi(5/2 5/3 | 3)
5/2.10/3.5/3.10/3
gidhid
U70
hemi(5/2 5/3 | 5/3)
 
3/2.6.3.6
oho
U3
hemi(?)
3/2.10.3.10
seihid
U49
hemi(3 3/2 | 5)
5.6.5/4.6
gidhei
U65
hemi(5 5/4 | 3)
3.10/3.3/2.10/3
geihid
U71
hemi(3 3/2 | 5/3)

Приведённые формы

Эти многогранники генерируются построением Витхоффа с лишними гранями. Если фигура генерируется с помощью построения Витхоффа как соединение двух или трёх неидентичных компонент, операция «приведения» удаляет лишние грани (которые следует указать) из фигуры, оставляя только одну компоненту.

Витхофф Многогранник Лишние грани   Витхофф Многогранник Лишние грани   Витхофф Многогранник Лишние грани
3 2 3/2 |
4.6.4/3.6
cho
U15		 4{6/2}   4 2 3/2 |
4.8.4/3.8/7
sroh
U18		 8{6/2}   2 3/2 4/3 |
4.8/3.4/3.8/5
groh
U21		 8{6/2}
5 5/2 2 |
4.10.4/3.10/9
sird
U39		 12{10/2}   5 3 3/2 |
10.6.10/9.6/5
siddy
U50		 20{6/2}   3 5/2 2 |
6.4.6/5.4/3
ri
U56		 12{10/2}
5 5/2 3/2 |
3/2.10.3.10
seihid
U49		 id + sidhid   5 5/2 3/2 |
5/4.10.5.10
sidhid
U51		 id + seihid   5 3 5/4 |
10.6.10/9.6/5
siddy
U50		 12{10/4}
3 5/2 5/3 |
6.10/3.6/5.10/7
giddy
U63		 12{10/2}   5 2 3/2 |
4.10/3.4/3.10/9
sird
U39		 20{6/2}   3 5/2 5/4 |
5.6.5/4.6
gidhei
U65		 did + sidhei
3 5/2 5/4 |
5/2.6.5/3.6
sidhei
U62		 did + gidhei   3 5/3 3/2 |
6.10/3.6/5.10/7
giddy
U63		 20{6/2}   3 2 5/4 |
6.4.6/5.4/3
ri
U56		 12{10/4}
2 5/3 3/2 |
4.10/3.4/3.10/7
gird

U73

 20{6/2}   5/3 3/2 5/4 |
3.10/3.3/2.10/3
geihid
|U71		 gid + gidhid   5/3 3/2 5/4 |
5/2.10/3.5/3.10/3
gidhid
U70		 gid + geihid
2 5/3 5/4 |
4.10/3.4/3.10/7
gird

U73

 12{10/4}                

Тетрагемигексаэдр (thah, U4) является также приведённой формой {3/2}-купола (обратный треугольный купол, ratricu) по {6/2}.

Другие формы

Эти два однородных многогранника нельзя получить с помощью построения Витхоффа. Это множество многогранников принято называть «невитхоффовыми». Вместо треугольной фундаментальной области витхоффовых однородных многогранников эти два имеют четырёхугольную фундаментальную область.

Многогранник Скиллинга не дан в списке Маедера, поскольку он принадлежит к экзотическим однородным многогранникам, у которых рёбра полностью совпадают. Это верно также для некоторых вырожденных многогранников, перечисленных выше, таких как малый составной икосододекаэдр. Такая интерпретация совпадающих рёбер позволяет этим фигурам оставаться биметорными (греч.: bi + methoric = два + ребро), то есть имеющими две грани на ребро. Без удвоения рёбер эти тела превратились бы в тетра-, гекса-, окта-, дека- или додекаметорные фигуры, которые обычно исключаются из списка однородных многогранников. Фигура Скиллинга является тетраметорной [4].

(p q r s) | p q r s
(4.p.4.q.4.r.4.s)/2		 | (p) q (r) s
(p3.4.q.4.r3.4.s.4)/2
(3/2 5/3 3 5/2)
(4.3/2.4.5/3.4.3.4.5/2)/2
gidrid
U75
(3/23.4.5/3.4.33.4.5/2.4)/2
gidisdrid
Скиллинга

Примечания
  1. Maeder, 2000.
  2. Дьяконов, 2008.
  3. Coxeter, 1973.
  4. Guy Inchbald – Trimethoric (and trisynaptic) polyhedra

Литература
  • Roman E. Maeder. Computer Science with Mathematica. — Cambridge University Press, 2000. — ISBN 0-521-63172-6,0-521-66395-4.
  • Дьяконов В. П. Mathematica 5.1/5.2/6. Программирование и математические вычисления. — М.: ДМК-Пресс, 2008. — ISBN 5-94074-405-2.
  • H. S. M. Coxeter. Regular Polytopes. — 3rd edition. — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.

Ссылки

Richard Klitzing: Polyhedra by

Zvi Har'El:

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.