Большой вывернутый обратноплосконосый икосододекаэдр
Большой (вывернутый) обратноплосконосый икосододекаэдр — это невыпуклый однородный многогранник, имеющий индекс U74. Его символ Шлефли — s{3/2,5/3}.
| Большой вывернутый обратноплосконосый икосододекаэдр | |||
|---|---|---|---|
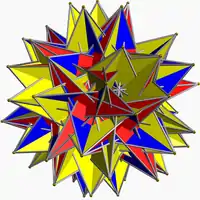 | |||
| Тип | Однородный звёздчатый многогранник | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани | 98 | ||
| Двойственный многогранник | Большой пятиугольный шестидесятигранник | ||
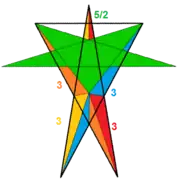 (34.5/2)/2 |
|||
| Классификация | |||
| Обозначения | U74,K79, C90 | ||
| Символ Шлефли | s{3/2,5/3} | ||
| Символ Витхоффа | |3/2 5/3 2 | ||
| Группа симметрии | I, [5,3]+, 532 | ||
Декартовы координаты
Декартовы координаты вершин большого обратноплосконосого икосододекаэдра все являются чётными перестановками
- (±2α, ±2, ±2β),
- (±(α−βτ−1/τ), ±(α/τ+β−τ), ±(−ατ−β/τ−1)),
- (±(ατ−β/τ+1), ±(−α−βτ+1/τ), ±(−α/τ+β+τ)),
- (±(ατ−β/τ−1), ±(α+βτ+1/τ), ±(−α/τ+β−τ)) and
- (±(α−βτ+1/τ), ±(−α/τ−β−τ), ±(−ατ−β/τ+1)),
с чётным числом знаков плюс, где
- α = ξ−1/ξ
и
- β = −ξ/τ+1/τ2−1/(ξτ),
где τ = (1+√5)/2 — золотое сечение, а ξ — наименьший положительный вещественный нуль функции ξ3−2ξ=−1/τ, а именно
что примерно равно 0,3264046. Если взять нечётные перестановки координат выше с нечётным числом знаков плюс, получим другую, энантиоморфную, форму. Если взять нечётные перестановки с чётным числом знаков плюс или наоборот, получим те же тела, повёрнутые на 90 градусов.
Радиус описанной сферы для тела с единичным ребром равен
- ,
где — подходящий нуль функции . Четыре положительных вещественных корня уравнения шестой степени в
являются радиусами описанных сфер плосконосого додекаэдра (U29), большого плосконосого икосододекаэдра (U57), большого вывернутого плосконосого икосододекаэдра (U69) и большого обратноплосконосого икосододекаэдра (U74).
См. также
- Список однородных многогранников
- Большой плосконосый икосододекаэдр
- Большой вывернутый плосконосый икосододекаэдр
Примечания
Литература
Ссылки
- Weisstein, Eric W. Great retrosnub icosidodecahedron (англ.) на сайте Wolfram MathWorld.
- https://web.archive.org/web/20171110075259/http://gratrix.net/polyhedra/uniform/summary/