Призматический однородный многогранник

Призматический однородный многогранник — однородный многогранник с диэдральной симметрией. Они образуют два бесконечных семейства, однородные призмы и однородные антипризмы. Все они имеют вершины на двух параллельных плоскостях, а потому все они являются призматоидами.

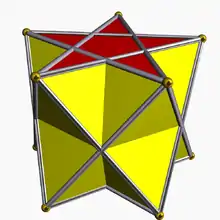
Пентаграммная антипризма состоит из двух правильных пентаграмм и 10 равнобедренных треугольников.

Вершинная конфигурация и группы симметрии

Поскольку они являются изогональными (вершинно-транзитивными), их расположение вершин однозначно соответствует группам симметрии.

Разница между призматическими и антипризматическими группами симметрии заключается в том, что Dph имеет рёбра, связывающие вершины на двух плоскостях, перпендикулярные этим плоскостям, что задаёт плоскость симметрии, параллельную многоугольникам, в то время как Dpd имеет скрещивающиеся рёбра, что даёт вращательную симметрию. Каждое тело имеет p плоскостей отражений, которые содержат p-кратные оси многоугольников.

Группа симметрии Dph содержит центральную симметриию тогда и только тогда, когда p чётно, в то время как Dpd содержит центральную симметрию тогда и только тогда, когда p нечётно.

Список

Существуют:

  • Призмы для каждого рационального p/q > 2 с группой симметрии Dph;
  • Антипризмы для каждого рационального p/q > 3/2 с группой симметрии Dpd, если q нечётно и Dph если чётно.

Если p/q является целым числом, т.е. q = 1, призма или антипризма выпукла. (Дробь всегда считается несократимой.)

Антипризма с p/q < 2 является самопересекающейся или вырожденной, её вершинная фигура походит на галстук-бабочку. С p/q ≤ 3/2 однородных антипризм не существует, поскольку их вершинная фигура нарушила бы неравенство треугольника.

Рисунки

Замечание: Тетраэдр, куб и октаэдр перечислены ниже как имеющие диэдральную симметрию (как диагональная антипризма, квадратная призма и треугольная антипризма соответственно), хотя, при однородной раскраске, тетраэдр также имеет тетраэдральную симметрию, а куб и октаэдр имеют октаэдральную симметрию.

Группа симметрии Выпуклый Звёздчатые формы
d2d
[2+,2]
(2*2)
3.3.3
d3h
[2,3]
(*223)
3.4.4
d3d
[2+,3]
(2*3)
3.3.3.3
d4h
[2,4]
(*224)
4.4.4
d4d
[2+,4]
(2*4)
3.3.3.4
d5h
[2,5]
(*225)
4.4.5
4.4.5/2
3.3.3.5/2
d5d
[2+,5]
(2*5)
3.3.3.5
3.3.3.5/3
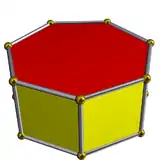
d6h
[2,6]
(*226)
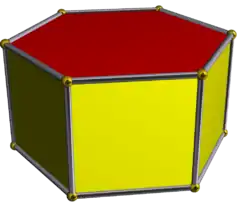4.4.6
d6d
[2+,6]
(2*6)
3.3.3.6
d7h
[2,7]
(*227)
4.4.7
4.4.7/2
4.4.7/3
3.3.3.7/2
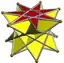3.3.3.7/4
d7d
[2+,7]
(2*7)
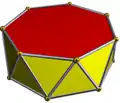3.3.3.7
3.3.3.7/3
d8h
[2,8]
(*228)
4.4.8
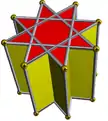4.4.8/3
d8d
[2+,8]
(2*8)
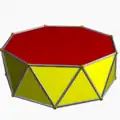3.3.3.8
3.3.3.8/3
3.3.3.8/5
d9h
[2,9]
(*229)
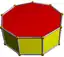4.4.9
4.4.9/2
4.4.9/4
3.3.3.9/2
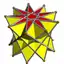3.3.3.9/4
d9d
[2+,9]
(2*9)
3.3.3.9
3.3.3.9/5
d10h
[2,10]
(*2.2.10)
4.4.10
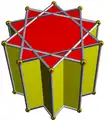4.4.10/3
d10d
[2+,10]
(2*10)
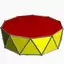3.3.3.10
3.3.3.10/3
d11h
[2,11]
(*2.2.11)
4.4.11
4.4.11/2
4.4.11/3
4.4.11/4
4.4.11/5
3.3.3.11/2
3.3.3.11/4
3.3.3.11/6
d11d
[2+,11]
(2*11)
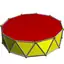3.3.3.11
3.3.3.11/3
3.3.3.11/5
3.3.3.11/7
d12h
[2,12]
(*2.2.12)
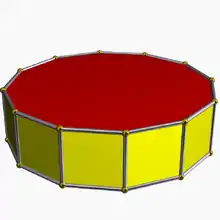4.4.12
4.4.12/5
d12d
[2+,12]
(2*12)
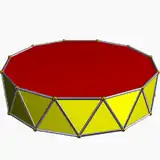3.3.3.12

3.3.3.12/5
3.3.3.12/7

3.3.3.12/7

...

См. также

Примечания

    Литература
    • H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller. Uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, вып. 916. — С. 401–450. — ISSN 0080-4614. — doi:10.1098/rsta.1954.0003. — .
    • P. Cromwell. Polyhedra. — United Kingdom: Cambridge University Press, 1997. — С. 175. — ISBN 0-521-55432-2.
    • John Skilling. Uniform Compounds of Uniform Polyhedra // Mathematical Proceedings of the Cambridge Philosophical Society. — 1976. — Т. 79, вып. 3. — С. 447–457. — doi:10.1017/S0305004100052440..

    Ссылки
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.