Диаграмма Шлегеля

Диаграмма Шлегеля — проекция политопа из в через точку за одной из его граней. Результирующая фигура в комбинаторно эквивалентна исходному политопу. Диаграмма названа по имени Виктора Шлегеля, который предложил в 1886 году этот метод для изучения комбинаторных и топологических свойств политопов. В размерностях 3 и 4 диаграммы Шлегеля являются проекцией (3-мерного) многогранника в плоскую фигуру и проекцией 4-мерного многогранника в трёхмерное пространство соответственно. Как таковые, диаграммы Шлегеля часто используются для визуализации четырёхмерных многогранников.

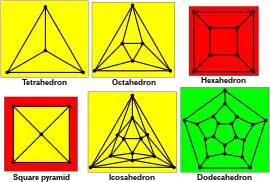
Примеры, раскрашенные по числу рёбер на каждой грани. Жёлтые треугольники, красные квадраты и зелёные пятиугольники.
Тессеракт, спроецированный в 3-мерное пространство как диаграмма Шлегеля. Видно 8 кубических ячеек — одна в центре, по одной для шести граней центрального куба и одна внешняя грань.

Построение

Наиболее элементарное описание диаграммы Шлегеля для многогранника дано Дунканом Соммервиллем (Duncan Sommerville)[1]:

Очень полезным метод представления выпуклого многогранника является плоская проекция. Если эта проекция произведена из внешней точки, поскольку каждый луч пересекает многогранник дважды, он будет представлен многоугольной областью, разделённой дважды на многоугольники. Всегда существует подходящий выбор центра проекции, чтобы проекция одной из граней содержала проекции всех остальных граней. Это называется диаграммой Шлегеля многогранника. Диаграмма Шлегеля полностью представляет морфологию многогранника. Иногда удобно сделать проекцию многогранника из вершины. Вершина проектируется в бесконечность и не появляется на диаграмме, рёбра, идущие к ней представляются лучами, уходящими в бесконечность.

Соммервиль рассматривал также случай симплекса в четырёхмерном пространстве[2]: «Диаграмма Шлегеля симплекса в S4 является тетраэдром, разделённым на четыре тетраэдра». В более общем случае, политоп в n-мерном пространстве имеет диаграмму Шлегеля, построенную с помощью перспективной проекции через точку вне политопа, над центром грани. Все вершины и рёбра политопа проектируются на гиперплоскость этой грани. Если политоп выпуклый, существует точка около грани, при которой эта грань становится внешней, а все остальные грани оказываются внутри неё, при этом рёбра пересекаться не будут.

Примеры
Додекаэдр Стодвадцатиячейник

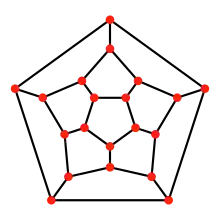12 пятиугольных граней на плоскости
120 додекаэдров (ячеек) в 3-мерном пространстве

Различные виды визуализации икосаэдра


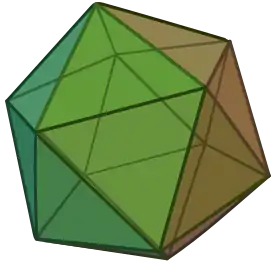перспектива
развёртка
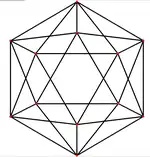проекция

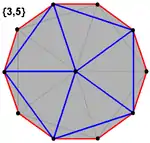Петри
Шлегель
Вершинная фигура

См. также
  • Развёртка — другой подход к визуализации через многогранники меньших размерностей, при которой грани разъединяются и разгибаются, пока все грани не окажутся в одной гиперплоскости. Такое представление сохраняет геометрические размеры и форму, но при этом труднее рассмотреть топологические связи.

Примечания
  1. Sommervill, 1929, p. 100.
  2. Sommervill, 1929, p. 101.

Литература
  • Duncan Sommervill. Introduction to the Geometry of N Dimensions. — E. P. Dutton, 1929. Репринт 1958 издательством Dover Books.
  • Victor Schlegel. Theorie der homogen zusammengesetzten Raumgebilde. — Druck von E. Blochmann & Sohn in Dresden, 1883. — Т. Nova Acta, Ksl. Leop.-Carol. Deutsche Akademie der Naturforscher XLIV. Архивная копия от 12 марта 2007 на Wayback Machine
  • Victor Schlegel. Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper. — Waren, 1886.
  • H. S. M. Coxeter. Regular Polytopes. — Methuen and Co., 1948. — С. 242.
    • Regular Polytopes. — 3rd edition. — Dover edition, 1973. — ISBN 0-486-61480-8.
  • Branko Grünbaum. Convex polytopes / Volker Kaibel, Victor Klee, Günter M. Ziegler. — 2nd. — New York, London: Springer-Verlag, 2003. — ISBN 0-387-00424-6.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.