Почти многогранник Джонсона
Почти многогранник Джонсона — строго выпуклый многогранник, в котором грани близки к правильным многоугольникам, но некоторые или все из них не совсем правильные. Понятие обобщает многогранники Джонсона и «часто могут физически построены без заметного отличия» неправильных граней от правильных.[1] Точное число «почти» многогранников Джонсона зависит от требований, насколько точно грани приближаются к правильным многоугольникам.
Примеры
| Название Название по Конвею |
Рисунок | Вершинная конфигурация |
V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | F12 | Симметрия |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Усечённый триакистетраэдр t6kT |
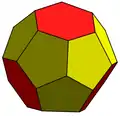 |
4 (5.5.5) 24 (5.5.6) |
28 | 42 | 16 | 12 | 4 | Td, [3,3] порядок 24 | |||||
| Скошенный куб cC |
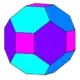 |
24 (4.6.6) 8 (6.6.6) |
32 | 48 | 18 | 6 | 12 | Oh, [4,3] порядок 48 | |||||
| -- | 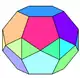 |
12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5) |
30 | 54 | 26 | 12 | 12 | 2 | D6h, [6,2] порядок 24 | ||||
| -- |  |
6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5) |
27 | 51 | 26 | 14 | 12 | D3h, [3,2] порядок 12 | |||||
| Четвертованный додекаэдр |  |
4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5) |
28 | 54 | 28 | 16 | 12 | Td, [3,3] порядок 24 | |||||
| Скошенный додекаэдр cD |
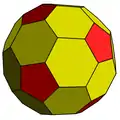 |
60 (5.6.6) 20 (6.6.6) |
80 | 120 | 42 | 12 | 30 | Ih, [5,3] порядок 120 | |||||
| Полностью усечённый усечённый икосаэдр rtI |
 |
60 (3.5.3.6) 30 (3.6.3.6) |
90 | 180 | 92 | 60 | 12 | 20 | Ih, [5,3] порядок 120 | ||||
| Усечённый усечённый икосаэдр ttI |
 |
120 (3.10.12) 60 (3.12.12) |
180 | 270 | 92 | 60 | 12 | 20 | Ih, [5,3] порядок 120 | ||||
| Расширенный усечённый икосаэдр etI |
 |
60 (3.4.5.4) 120 (3.4.6.4) |
180 | 360 | 182 | 60 | 90 | 12 | 20 | Ih, [5,3] порядок 120 | |||
| Плосконосый полностью усечённый усечённый икосаэдр stI |
 |
60 (3.3.3.3.5) 120 (3.3.3.3.6) |
180 | 450 | 272 | 240 | 12 | 20 | I, [5,3]+ порядок 60 |
Почти многогранники Джонсона с копланарными гранями
Некоторые кандидаты в почти многогранники Джонсона имеют копланарные грани. Эти многогранники можно чуть деформировать так, что грани будут сколь угодно близки к правильным многоугольникам. Эти случаи используют вершинные фигуры 4.4.4.4 квадратной мозаики, вершинные фигуры 3.3.3.3.3.3 треугольной мозаики, а также ромбы с углом 60º, делённые на два правильных треугольника, или трапеции с углом 60º как три правильных треугольника.
Примеры: 3.3.3.3.3.3
 Ромбическая призма
Ромбическая призма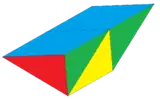
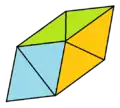 Треугольный трапецоэдр
Треугольный трапецоэдр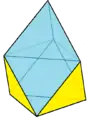 Скрученно удлинённая треугольная пирамида
Скрученно удлинённая треугольная пирамида Триангулированный одноусечённый тетраэдр
Триангулированный одноусечённый тетраэдр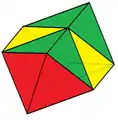 Удлинённый октаэдр
Удлинённый октаэдр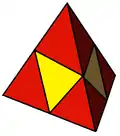 Триангулированный тетраэдр
Триангулированный тетраэдр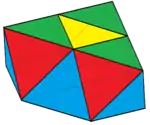 Наращенный треугольный купол
Наращенный треугольный купол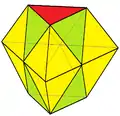 Триангулированная усечённая бипирамида
Триангулированная усечённая бипирамида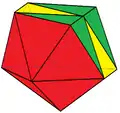

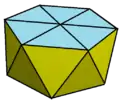
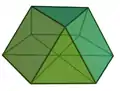

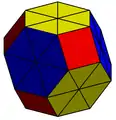
4.4.4.4
3.4.6.4:
 Шестиугольный купол
Шестиугольный купол
(вырожденный)
См. также
Примечания
- Craig S. Kaplan, George W. Hart. Bridges: Mathematical Connections in Art, Music and Science. — 2001.
