Клин (геометрия)
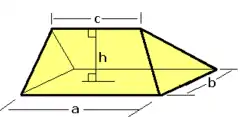
Клин — многогранник, имеющий две треугольные и три трапециевидные грани. Клин имеет пять граней, девять рёбер и шесть вершин.
| Клин | |
|---|---|
 | |
| Грани | 2 треугольника, 3 четырёхугольника |
| Рёбер | 9 |
| Вершин | 6 |
| Двойственный многогранник | Треугольная бипирамида |
| Свойства | выпуклый |
Клин является подклассом призматоидов, если рассматривать верхнее ребро как вырожденную грань (у призматоидов две грани параллельны).
Клин можно также понимать как двуугольный купол.
Сравнение с другими многогранниками:
- Если одна грань параллелепипеда вырождается в отрезок, получится клин.
- Прямоугольная пирамида является клином, в котором одно из рёбер вырождается в точку.
Объём
Объём клина с прямоугольным основанием вычисляется по формуле
где стороны основания равны a, b и c равно длине верхнего ребра, параллельного a, а h является высотой от основания до верхнего ребра.
Примеры
Клинья можно получить разрезанием других многогранников. Например, додекаэдр можно разбить на центральный куб и 6 клиньев, накрывающих грани куба. Ориентации клиньев выбираются таким образом, что треугольные и трапециевидные грани соединяются и образуют правильные пятиугольники.
Треугольная призма является специальным случаем клина с двумя параллельными треугольными гранями.
Два тупых клина можно получить, разрезав пополам правильный тетраэдр плоскостью, параллельной двум противоположным сторонам.
 Треугольная призма (Параллельный треугольный клин) |
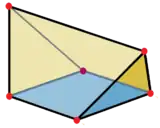 Тупоугольный клин как усечённый наполовину правильный тетраэдр |
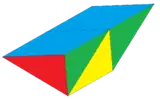 Клин, построенный из 8 треугольных граней и 2 квадратов. Его можно рассматривать как тетраэдр, наращенный двумя квадратными пирамидами. |
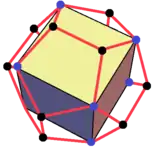 Додекаэдр можно разложить на центральный куб и 6 клиньев на его 6 квадратных гранях. |
Литература
- Harris, J. W., Stocker, H. §4.5.2 // Handbook of Mathematics and Computational Science. — New York: Springer, 1998. — С. 102. — ISBN 978-0-387-94746-4.
