Циклическое число
Циклическое число — целое число, циклические перестановки цифр которого являются произведениями этого числа на последовательные числа. Наиболее известный пример такого числа — 142857:
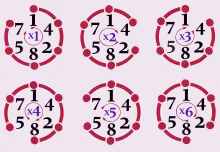
- 142857 × 1 = 142857
- 142857 × 2 = 285714
- 142857 × 3 = 428571
- 142857 × 4 = 571428
- 142857 × 5 = 714285
- 142857 × 6 = 857142
Детали
Чтобы число было циклическим, требуется, чтобы умножение на последовательные числа давала перестановки цифр числа. Так, число 076923 не считается циклическим, поскольку, хотя все циклические перестановки являются произведением числа на некоторые целые множители, эти множители не являются последовательными целыми числами:
- 076923 × 1 = 076923
- 076923 × 3 = 230769
- 076923 × 4 = 307692
- 076923 × 9 = 692307
- 076923 × 10 = 769230
- 076923 × 12 = 923076
Обычно исключаются следующие типичные случаи:
- Отдельные цифры, например, 5
- повторяющиеся цифры, например, 555
- повторяющиеся циклические числа, такие как 142857142857
Если в числах не разрешены ведущие нули, то 142857 является единственным циклическим числом в десятичной системе счисления, что определяется необходимой структурой чисел, описанной в следующей секции. Если ведущие нули разрешены, последовательность циклических чисел начинается с:
- (106−1) / 7 = 142857 (6 цифр)
- (1016−1) / 17 = 0588235294117647 (16 цифр)
- (1018−1) / 19 = 052631578947368421 (18 цифр)
- (1022−1) / 23 = 0434782608695652173913 (22 цифры)
- (1028−1) / 29 = 0344827586206896551724137931 (28 цифр)
- (1046−1) / 47 = 0212765957446808510638297872340425531914893617 (46 цифр)
- (1058−1) / 59 = 0169491525423728813559322033898305084745762711864406779661 (58 цифр)
- (1060−1) / 61 = 016393442622950819672131147540983606557377049180327868852459 (60 цифр)
- (1096−1) / 97 = 010309278350515463917525773195876288659793814432989690721649484536082474226804123711340206185567 (96 цифр)
Связь с повторяющимися десятичными числами
Циклические числа связаны с периодическими десятичными дробями долей единицы. Циклическое число длины L имеет десятичное представление
- 1/(L + 1).
Наоборот, если десятичный период числа 1 /p (где p простое) равен[1]
- p − 1,
то цифры представляют циклическое число.
Например:
- 1/7 = 0.142857 142857….
Умножение этой дроби даёт циклическую перестановку:
- 1/7 = 0.142857 142857…
- 2/7 = 0.285714 285714…
- 3/7 = 0.428571 428571…
- 4/7 = 0.571428 571428…
- 5/7 = 0.714285 714285…
- 6/7 = 0.857142 857142….
Формат циклических чисел
Используя связь с долями единицы, можно показать, что циклические числа имеют вид частного Ферма
- ,
где b — основание системы счисления (10 для десятичной системы), а p — простое, которое не делит b. (Простые числа p, которые образуют циклические числа по основанию b, называются полно-повторными простыми или длинными простыми по основанию b [2]).
Например, для b = 10, p = 7 даёт циклическое число 142857, а для b = 12, p = 5 даёт циклическое число 2497.
Не все значения p дают циклические числа согласно этой формуле. Например, для b = 10, p = 13 даёт 07692307692310, а для b = 12, p = 19 даёт 076B45076B45076B4512. Эти числа не являются циклическими, поскольку состоят из повторяющихся последовательностей.
Первые значения p, для которых формула даёт циклические числа по десятичному основанию (b = 10) (последовательность A001913 в OEIS)
- 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983, …
Для b = 12 (двенадцатеричная система) эти значения p равны (последовательность A019340 в OEIS)
- 5, 7, 17, 31, 41, 43, 53, 67, 101, 103, 113, 127, 137, 139, 149, 151, 163, 173, 197, 223, 257, 269, 281, 283, 293, 317, 353, 367, 379, 389, 401, 449, 461, 509, 523, 547, 557, 569, 571, 593, 607, 617, 619, 631, 641, 653, 691, 701, 739, 751, 761, 773, 787, 797, 809, 821, 857, 881, 929, 953, 967, 977, 991, …
Для b = 2 (двоичная система) эти значения p равны (последовательность A001122 в OEIS)
- 3, 5, 11, 13, 19, 29, 37, 53, 59, 61, 67, 83, 101, 107, 131, 139, 149, 163, 173, 179, 181, 197, 211, 227, 269, 293, 317, 347, 349, 373, 379, 389, 419, 421, 443, 461, 467, 491, 509, 523, 541, 547, 557, 563, 587, 613, 619, 653, 659, 661, 677, 701, 709, 757, 773, 787, 797, 821, 827, 829, 853, 859, 877, 883, 907, 941, 947, …
Для b = 3 (троичная система) эти значения p равны (последовательность A019334 в OEIS)
- 2, 5, 7, 17, 19, 29, 31, 43, 53, 79, 89, 101, 113, 127, 137, 139, 149, 163, 173, 197, 199, 211, 223, 233, 257, 269, 281, 283, 293, 317, 331, 353, 379, 389, 401, 449, 461, 463, 487, 509, 521, 557, 569, 571, 593, 607, 617, 631, 641, 653, 677, 691, 701, 739, 751, 773, 797, 809, 811, 821, 823, 857, 859, 881, 907, 929, 941, 953, 977, …
Не существует таких чисел p в шестнадцатеричной системе.
Известные схемы таких последовательностей получаются из алгебраической теории чисел, а именно, эта последовательность является множество простых p, таких что b является первообразным корнем по модулю p.
Построение циклических чисел
Циклические числа можно получить следующей процедурой:
Пусть b — основание системы счисления (10 для десятичных чисел)
Пусть p — простое число, не являющееся делителем b.
Положим t = 0.
Положим r = 1.
Положим n = 0.
цикл:
- Положим t = t + 1
- Положим x = r · b
- Положим d = целая часть(x / p)
- Положим r = x mod p
- Положим n = n · b + d
- Если r ≠ 1, переходим в начало цикла.
Если t = p − 1, то n является циклическим числом.
Процедура работает путём вычисления цифр дроби 1 /p по основанию b по алгоритму деления столбиком. На каждом шаге r является остатком, а d является очередной цифрой.
Шаг
- n = n · b + d
просто обеспечивает сборку цифр числа. Для компьютеров, не имеющих возможности вычислений с целыми числами очень большого размера, эти цифры можно просто отправлять на печать или собирать другим способом.
Заметим, что при достижении t границы p/2 получившееся число должно быть циклическим и необходимости вычислять дальнейшие цифры нет.
Свойства циклических чисел
Примечание: Ниже нижний индекс означает основание. Так, 14210 означает число 142 по основанию 10, а 1425 означает число 142 по основанию 5 (то есть 4710).
- Если умножить число на генерирующее простое, получим последовательность цифр ́base−1' (9 в случае десятичного основания). 14285710 × 7 = 99999910.
- Если разбить число на группы цифр (по две, три, четыре м т.д. цифры), а затем сложить полученные числа, получим последовательности девяток. 14 + 28 + 57 = 99, 142 + 857 = 999, 1428 + 5714+ 2857 = 9999 и т. д. … (Это частный случай теоремы Миди.)
- Все циклические числа делятся на ́base−1' (9 в случае десятичного основания).
Сколько циклических чисел?
Количество циклических чисел, не превышающих 10n, для натуральных n образуют последовательность (последовательность A086018 в OEIS):
- 1, 9, 60, 467, 3617, 25883, 248881, 2165288, 19016617…
Была высказана гипотеза (пока не доказана), что существует бесконечное множество циклических чисел[2]. Согласно гипотезе Эмиля Артина[3] эта последовательность содержит 37.395..% простых чисел (для b из последовательности A085397; последовательность A085397 в OEIS).
Другие системы счисления
Используя вышеприведённую технику, можно найти циклические числа в других системах счисления.
В двоичной системе последовательность циклических чисел начинается с: (последовательность A001122 в OEIS)
- 112 =310 → 012
- 1012 = 510 → 00112
- 10112 = 1110 → 00010111012
- 11012 = 1310 → 0001001110112
- 100112 =1910 → 0000110101111001012
- 111012 =2910 → 00001000110100111101110010112
- 1001012 = 3710 → 0000011011101011001111100100010100112
В троичной системе: (последовательность A019334 в OEIS)
- 23 =210 → 13
- 123 = 510 → 01213
- 213 = 710→ 0102123
- 1223 = 1710 → 00112021221102013
- 2013 =1910 → 0011021002211201223
- 10023 = 2910 → 00022101020111222001212021113
- 10113 = 3110 → 0002121112210202220101110012023
В четверичной системе:
- (циклических чисел нет)
В пятеричной системе: (последовательность A019335 в OEIS)
- 25 = 210 → 25
- 35 = 310 → 135
- 125 = 710 → 032412 5
- 325 = 1710 → 01213402432310425
- 435 = 2310 → 01020413321434240311235
- 1225 = 3710 → 0031421220401133424413023224043311025
- 1335 = 4310 → 0024231412234340431114420213032210104013335
В шестеричной системе: (последовательность A167794 в OEIS)
- 156 = 1110 → 03134524216
- 216 = 1310 → 0243405312156
- 256 = 1710 → 02041224535143316
- 1056 = 4110 → 00513354124403302344550422014311522532116
- 1356 = 5910 → 00335444022351041343242503014552201115332045142123130525416
- 1416 = 6110 → 0033125040441544530143423202205522430515114011025412132353356
- 2116 =7910 → 002422325434441304033512354102140052450553133230121114251522043201453415503105
В семеричной системе: (последовательность A019337 в OEIS)
- 27 = 210 → 37
- 57 = 510 → 12547
- 147 = 1110 → 04311623557
- 167 = 1310 → 0352456314217
- 237 = 1710 → 02611434640552327
- 327 = 2310 → 02062511343646041553237
- 567 = 4110 → 01123632621352022505655430340453146441617
В восьмеричной системе: (последовательность A019338 в OEIS)
- 38 = 310 → 258
- 58 = 510 → 14638
- 138 = 1110 → 05642721358
- 358 = 2910 → 02151734541064756260432367138
- 658 = 5310 → 01152207175453361404651034766255706023244163731267438
- 738 = 5910 → 01053307457565116064042554362767244703202126617137352234158
- 1238 = 8310 → 00612627103665763523215702240305313441732771651506741120142545620755374724643360458
В девятеричной системе:
- 29 = 210 → 49
- (других нет)
В одиннадцатеричной системе 11: (последовательность A019339 в OEIS)
- 211 = 210 → 511
- 311 = 310 → 3711
- 1211 = 1310 → 093425A1768511
- 1611 = 1710 → 07132651A397845911
- 2111 = 2310 → 05296243390A581486771A11
- 2711 = 2910 → 04199534608387A69115764A272311
- 2911 = 3110 → 039A32146818574A7107896429253611
В двенадцатеричной системе: (последовательность A019340 в OEIS)
- 512 = 510 → 249712
- 712 = 710 → 186A3512
- 1512 = 1710 → 08579214B36429A712
- 2712 = 3110 → 0478AA093598166B74311B28623A5512
- 3512 = 4110 → 036190A653277397A9B4B85A2B1568944824120712
- 3712 = 4310 → 0342295A3AA730A068456B879926181148B1B5376512
- 4512 = 5310 → 02872B3A23205525A784640AA4B9349081989B6696143757B11712
В тринадцатеричной системе: (последовательность A019341 в OEIS)
- 213 = 210 → 613
- 513 = 510 → 27A513
- B13 = 1110 → 12495BA83713
- 1613 = 1910 → 08B82976AC414A356213
- 2513 = 3110 → 055B42692C21347C7718A63A0AB98513
- 2B13 = 3710 → 0474BC3B3215368A25C85810919AB79642A713
- 3213 = 4110 → 04177C08322B13645926C8B550C49AA1B96873A613
В 14-ричной системе: (последовательность A019342 в OEIS)
- 314 = 310 → 4914
- 1314 = 1710 → 0B75A9C4D268341914
- 1514 = 1910 → 0A45C7522D398168BB14
- 1914 = 2310 → 0874391B7CAD569A4C261314
- 2114 = 2910 → 06A89925B163C0D73544B82C7A1D14
- 3B14 = 5310 → 039AB8A075793610B146C21828DA43253D6864A7CD2C971BC5B514
- 4314 = 5910 → 03471937B8ACB5659A2BC15D09D74DA96C4A62531287843B21C80D406914
В 15-ричной системе: (последовательность A019343 в OEIS)
- 215 = 210 → 715
- D15 = 1310 → 124936DCA5B815
- 1415 = 1910 → 0BC9718A3E3257D64B15
- 1815 = 2310 → 09BB1487291E533DA67C5D15
- 1E15 = 2910 → 07B5A528BD6ACDE73949C631842115
- 2715 = 3710 → 061339AE2C87A8194CE8DBB540C26746D5A215
- 2B15 = 4110 → 0574B51C68BA922DD80AE97A39D286345CC116E415
- (циклических чисел нет)
В 17-ричной системе: (последовательность A019344 в OEIS)
- 217 = 210 → 817
- 317 = 310 → 5B17
- 517 = 510 → 36DA17
- 717 = 710 → 274E9C17
- B17 = 1110 → 194ADF7C6317
- 1617 = 2310 → 0C9A5F8ED52G476B1823BE17
- 1E17 = 3110 → 09583E469EDC11AG7B8D2CA7234FF617
В 18-ричной системе: (последовательность A019345 в OEIS)
- 518 = 510 → 3AE718
- B18 = 1110 → 1B834H69ED18
- 1B18 = 2910 → 0B31F95A9GDAE4H6EG28C781463D18
- 2118 = 3710 → 08DB37565F184FA3G0H946EACBC2G9D27E1H18
- 2718 = 4310 → 079B57H2GD721C293DEBCHA86CA0F14AFG5F8E436518
- 2H18 = 5310 → 0620C41682CG57EAFB3D4788EGHBFH5DGB9F51CA3726E4DA993118
- 3518 =5910 → 058F4A6CEBAC3BG30G89DD227GE0AHC92D7B53675E61EH19844FFA13H718
В 19-ричной системе: (последовательность A019346 в OEIS)
- 219 = 210 → 919
- 719 = 710 → 2DAG5819
- B19 = 1110 → 1DFA6H538C19
- D19 = 1310 → 18EBD2HA475G19
- 1419 = 2310 → 0FD4291C784I35EG9H6BAE19
- 1A19 = 2910 → 0C89FDE7G73HD1I6A9354B2BF15H19
- 1I19 = 3710 → 09E73B5C631A52AEGHI94BF7D6CFH8DG842119
В двадцатеричной системе: (последовательность A019347 в OEIS)
- 320 = 310 → 6D20
- D20 = 1310 → 1AF7DGI94C6320
- H20 = 1710 → 13ABF5HCIG984E2720
- 1320 = 2310 → 0H7GA8DI546J2C39B61EFD20
- 1H20 = 3710 → 0AG469EBHGF2E11C8CJ93FDA58234H5II7B720
- 2320 = 4310 → 0960IC1H43E878GEHD9F6JADJ17I2FG5BCB3526A4D20
- 2720 = 4710 → 08A4522B15ACF67D3GBI5J2JB9FEHH8IE974DC6G381E0H20
В 21-ричной системе: (последовательность A019348 в OEIS)
- 221 = 210 → A21
- J21 = 1910 → 1248HE7F9JIGC36D5B21
- 1221 = 2310 → 0J3DECG92FAK1H7684BI5A21
- 1821 = 2910 → 0F475198EA2IH7K5GDFJBC6AI23D21
- 1A21 = 3110 → 0E4FC4179A382EIK6G58GJDBAHCI6221
- 2B21 = 5310 → 086F9AEDI4FHH927J8F13K47B1KCE5BA672G533BID1C5JH0GD9J21
- 3821 = 7110 → 06493BB50C8I721A13HFE42K27EA785J4F7KEGBH99FK8C2DIJAJH356GI0ID6ADCF1G5D21
В 22-ричной системе: (последовательность A019349 в OEIS)
- 522 = 510 → 48HD22
- H22 = 1710 → 16A7GI2CKFBE53J922
- J22 = 1910 → 13A95H826KIBCG4DJF22
- 1922 = 3110 → 0FDAE45EJJ3C194L68B7HG722I9KCH22
- 1F22 = 3710 → 0D1H57G143CAFA2872L8K4GE5KHI9B6BJDEJ22
- 1J22 = 4110 → 0BHFC7B5JIH3GDKK8CJ6LA469EAG234I5811D92F22
- 2322 = 4710 → 0A6C3G897L18JEB5361J44ELBF9I5DCE0KD27AGIFK2HH722
В 23-ричной системе: (последовательность A019350 в OEIS)
- 223 = 210 → B23
- 323 =310 → 7F23
- 523 = 510 → 4DI923
- H23 = 1710 → 182G59AILEK6HDC423
- 2123 = 4710 → 0B5K1AHE496JD4KCGEFF3L0MBH2LC58IDG39I2A6877J1M23
- 2D23 = 5910 → 08M51CJK65AC1LJ27I79846E9H3BFME0HLA32GHCAL13KF4FDEIG8D5JB723
- 3K23 = 8910 → 05LG6ADG0BK9CL4910HJ2J8I21CF5FHD4327B8C3864EMH16GC96MB2DA1IDLM53K3E4KLA7H759IJKFBEAJEGI823
В 24-ричной системе: (последовательность A019351 в OEIS)
- 724 = 710 → 3A6KDH24
- B24 = 1110 → 248HALJF6D24
- D24 = 1310 → 1L795CM3GEIB24
- H24 = 1710 → 19L45FCGME2JI8B724
- 1724 = 3110 → 0IDMAK327HJ8C96N5A1D3KLG64FBEH24
- 1D24 = 3710 → 0FDEM1735K2E6BG54CN8A91MGKI3L9HC7IJB24
- 1H24 = 4110 → 0E14284G98IHDB2M5KBGN9MJLFJ7EF56ACL1I3C724
В 25-ричной системе:
- 225 = 210 → C25
- (других нет)
Заметим, что для троичного основания (b = 3) случай p = 2 даёт 1, что по правилам не является циклическим числом (тривиальный случай, одна цифра). Здесь же этот случай приведён для полноты теории, что все числа получаются таким способом.
Можно показать, что циклических чисел (отличных от тривиальных случаев с одной цифрой) не существует в системах счисления с квадратным основанием, то есть с основаниями 4, 9, 16, 25 и т. д..
См. также
- Периодическая дробь
- Малая теорема Ферма
- Циклическая перестановка цифр целых чисел
Примечания
Литература
- С.Л. Василенко. Сокрытые закономерности циклических числовых форм.
- Martin Gardner. Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments From Scientific American. — New York: The Mathematical Association of America, 1979. — С. 111–122.
- Мартин Гарднер. Лучшие математические игры и головоломки (Или самый настоящий математический цирк). — Москва: АСТ · Астрель, 2009. — С. 111–121. — ISBN 978-5-17-058244-0; 978-5-271-23247-3; УДК 159.9 ББК 88.37.
Литература для дальнейшего чтения
- Dan Kalman. Fractions with Cycling Digit Patterns // The College Mathematics Journal. — 1996. — Март (т. 27, вып. 2). — С. 109–115.
- John Leslie. The Philosophy of Arithmetic: Exhibiting a Progressive View of the Theory and Practice of ..... — Longman, Hurst, Rees, Orme, Brown, 1820. — ISBN 1-4020-1546-1.
- David Wells. The Penguin Dictionary of Curious and Interesting Numbers. — Penguin Press. — ISBN 0-14-008029-5.
Ссылки
- Weisstein, Eric W. Cyclic Number (англ.) на сайте Wolfram MathWorld.
- Youtube: «Cyclic Numbers — Numberphile»