Пентатопное число

${\displaystyle n}$-е по порядку пентатопное число определяется как сумма первых ${\displaystyle n}$ тетраэдральных чисел.

Начало последовательности пентатопных чисел:

${\displaystyle 1,5,15,35,70,126,210,330,495,715,\dots }$ (последовательность A000292 в OEIS).

${\displaystyle {\begin{array}{c}1\\1\quad 1\\1\quad 2\quad 1\\{\color {red}1}\quad 3\ \quad 3\quad 1\\{\color {green}1}\quad {\color {red}4}\ \quad 6\ \quad 4\quad 1\\1\quad {\color {green}5}\quad {\color {red}10}\quad 10\quad 5\quad 1\\1\quad 6\quad {\color {green}15}\quad {\color {red}20}\quad 15\quad 6\quad 1\\1\quad 7\quad 21\quad {\color {green}35}\quad {\color {red}35}\quad 21\quad 7\quad 1\\\end{array}}}$

Тетраэдральные (красные) и пентатопные (зелёные) числа в треугольнике Паскаля

Общая формула для ${\displaystyle n}$-го по порядку пентатопного числа ${\displaystyle PT_{n}}$:

${\displaystyle PT_{n}={\frac {n(n+1)(n+2)(n+3)}{24}}={n+3 \choose 4}}$

Пентатопные числа находятся на 5-й диагональной линии в треугольнике Паскаля (см. рисунок), под диагональю тетраэдральных чисел.

Два из каждых трёх пентатопных чисел (номера которых не делятся на 3) являются пятиугольными числами[1].

Ряд из обратных пентатопных чисел сходится[2]:

${\displaystyle {\frac {1}{1}}+{\frac {1}{5}}+{\frac {1}{15}}+{\frac {1}{35}}\dots ={\frac {4}{3}}}$

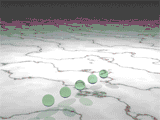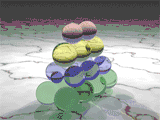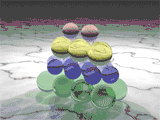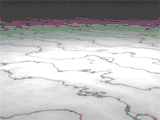
В биохимии пентатопные числа представляют количество возможных расположений ${\displaystyle n}$ различных белковых субъединиц в тетраэдральном белке.

• Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 30. — 320 с. — ISBN 5-09-006575-6.
• Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
• Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.

• Фигурные числа
• Pentatope Number  (англ.)