Центрированные многоугольные числа

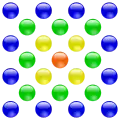
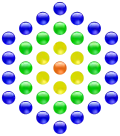
Центрированные многоугольные числа — это класс плоских ${\displaystyle k}$-угольных фигурных чисел (${\displaystyle k\geqslant 3}$), получаемый следующим геометрическим построением. Сначала на плоскости фиксируется некоторая центральная точка. Затем вокруг неё строится правильный ${\displaystyle k}$-угольник с ${\displaystyle k}$ точками вершин, каждая сторона содержит две точки (см. рисунок). Далее снаружи строятся новые слои ${\displaystyle k}$-угольников, причём каждая их сторона на новом слое содержит на одну точку больше, чем в предыдущем слое, то есть начиная со второго слоя каждый следующий слой содержит на ${\displaystyle k}$ больше точек, чем предыдущий. Общее число точек внутри каждого слоя и принимается в качестве центрированного многоугольного числа (точка в центре считается начальным слоем)[1].

Примеры построения центрированных многоугольных чисел:

Треугольные	Квадратные	Пятиугольные	Шестиугольные

Из построения видно, что центрированные многоугольные числа получаются как частичные суммы следующего ряда: ${\displaystyle 1+k+2k+3k+4k+\dots }$ (например, центрированные квадратные числа, для которых ${\displaystyle k=4,}$ образуют последовательность: ${\displaystyle 1,5,13,25,41\dots }$) Этот ряд можно записать как ${\displaystyle 1+k(1+2+3+4+\dots ).}$, откуда видно, что в скобках — порождающий ряд для классических треугольных чисел. Следовательно, каждая последовательность центрированных ${\displaystyle k}$-угольных чисел, начиная со 2-го элемента, может быть представлена как ${\displaystyle kT_{n}+1,}$ где ${\displaystyle T_{n}(n=1,2,3\dots )}$ — последовательность треугольных чисел. Например, центрированные квадратные числа — это учетверённые треугольные числа плюс 1, порождающий ряд для них имеет вид: ${\displaystyle 1+4+8+12\dots }$[2]

Общая формула[2] для ${\displaystyle n}$-го центрированного ${\displaystyle k}$-угольного числа ${\displaystyle C_{n}^{(k)}}$:

${\displaystyle C_{n}^{(k)}=1+k{\frac {n(n-1)}{2}}={\frac {kn^{2}-kn+2}{2}};\ n=1,2,3\dots }$

(ОЦФ)