Функция делителей
Фу́нкция дели́телей — арифметическая функция, связанная с делителями целого числа. Функция известна также под именем фу́нкция диви́зоров. Применяется, в частности, при исследовании связи дзета-функции Римана и рядов Эйзенштейна для модулярных форм. Изучалась Рамануджаном, который вывел ряд важных равенств в модульной арифметике и арифметических тождествах.
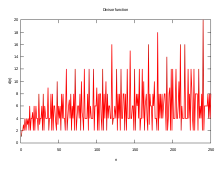
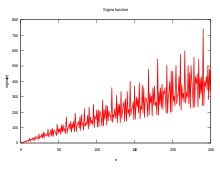
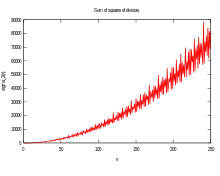
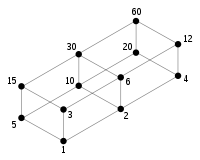
С этой функцией тесно связана суммирующая функция делителей, которая, как следует из названия, является суммой функции делителей.
Определение
Функция «сумма положительных делителей» σx(n) для вещественного или комплексного числа x определяется как сумма x-х степеней положительных делителей числа n. Функцию можно выразить формулой
где означает «d делит n». Обозначения d(n), ν(n) и τ(n) (от немецкого Teiler = делитель) используются также для обозначения σ0(n), или функции числа делителей [1][2]. Если x равен 1, функция называется сигма-функцией или суммой делителей[3], и индекс часто опускается, так что σ(n) эквивалентна σ1(n)[4].
Аликвотная сумма s(n) для n — это сумма собственных делителей (то есть всех делителей, за исключением самого n[5], и равна σ1(n) − n. Аликвотная последовательность для n образуется последовательным вычислением аликвотной суммы, то есть каждое последующее значение в последовательности равно аликвотной сумме предыдущего значения.
Примеры
Например, σ0(12) — количество делителей числа 12:
в то время как σ1(12) — сумма всех делителей:
и аликвотная сумма s(12) собственных делителей равна:
Таблица значений
| n | Делители | σ0(n) | σ1(n) | s(n) = σ1(n) − n | Комментарии |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | квадрат: значение σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное) |
| 2 | 1,2 | 2 | 3 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 3 | 1,3 | 2 | 4 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 4 | 1,2,4 | 3 | 7 | 3 | квадрат: σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное) |
| 5 | 1,5 | 2 | 6 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 6 | 1,2,3,6 | 4 | 12 | 6 | первое совершенное число: s(n) = n |
| 7 | 1,7 | 2 | 8 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 8 | 1,2,4,8 | 4 | 15 | 7 | степень 2: s(n) = n − 1 (почти совершенное) |
| 9 | 1,3,9 | 3 | 13 | 4 | квадрат: σ0(n) нечётно |
| 10 | 1,2,5,10 | 4 | 18 | 8 | |
| 11 | 1,11 | 2 | 12 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 12 | 1,2,3,4,6,12 | 6 | 28 | 16 | первое избыточное число: s(n) > n |
| 13 | 1,13 | 2 | 14 | 1 | простое: σ1(n) = 1+n, так что s(n) =1 |
| 14 | 1,2,7,14 | 4 | 24 | 10 | |
| 15 | 1,3,5,15 | 4 | 24 | 9 | |
| 16 | 1,2,4,8,16 | 5 | 31 | 15 | квадрат: σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное) |
Случаи , и так далее входят в последовательности A001157, A001158, A001159, A001160, A013954, A013955 …
Свойства
Для целых, не являющихся квадратами, каждый делитель d числа n имеет парный делитель n/d, а значит, всегда чётно для таких чисел. Для квадратов один делитель, а именно , не имеет пары, так что для них всегда нечётно.
Для простого числа p,
поскольку, по определению, простое число делится только на единицу и самого себя. Если pn# означает праймориал, то
Ясно, что и для всех .
Функция делителей мультипликативна, но не вполне мультипликативна.
Если мы запишем
- ,
где r = ω(n) — число простых делителей числа n, pi — i-й простой делитель, а ai — максимальная степень pi, на которую делится n, то
- ,
что эквивалентно:
Если положить x = 0, получим, что d(n) равно:
Например, число n = 24 имеет два простых делителя — p1 = 2 и p2 = 3. Поскольку 24 — это произведение 23×31, то a1 = 3 и a2 = 1.
Теперь мы можем вычислить :
Восемь делителей числа 24 — это 1, 2, 4, 8, 3, 6, 12, и 24.
Заметим также, что s(n) = σ(n) − n. Здесь s(n) обозначает сумму собственных делителей числа n, то есть делителей, за исключением самого числа n. Эта функция используется для определения совершенности числа — для них s(n) = n. Если s(n) > n, n называется избыточным, а если s(n) < n, n называется недостаточным.
Если n — степень двойки, то есть , то и s(n) = n — 1, что делает n почти совершенным.
Как пример, для двух простых p и q (где p < q), пусть
Тогда
и
где φ(n) — функция Эйлера.
Тогда корни p и q уравнения:
можно выразить через σ(n) и φ(n) :
Зная n и либо σ(n), либо φ(n) (или зная p+q и либо σ(n), либо φ(n)) мы легко можем найти p и q.
В 1984 году Хиз-Браун (Roger Heath-Brown) доказал, что
встречается бесконечно много раз.
Связь с рядами
Два ряда Дирихле, использующие функцию делителей:
и при обозначении d(n) = σ0(n) получим
и второй ряд,
Ряд Ламбера, использующий функцию делителей:
для любого комплексного |q| ≤ 1 и a.
Эта сумма появляется также в рядах Фурье для рядов Эйзенштейна и в инвариантах эллиптических функций Вейерштрасса.
Асимптотическая скорость роста
В терминах о-малое функция делителей удовлетворяет неравенству (см. стр. 296 книги Апостола[6])
- для всех
Северин Вигерт дал более точную оценку
С другой стороны, ввиду бесконечности количества простых чисел,
В терминах О-большое, Дирихле показал, что средний порядок функции делителей удовлетворяет следующему неравенству (см. теорему 3.3 книги Апостола)
- для всех
где — постоянная Эйлера — Маскерони.
Задача улучшить границу в этой формуле — это проблема Дирихле о делителях
Поведение сигма-функции неравномерно. Асимптотическую скорость роста сигма-функции можно выразить формулой:
где lim sup — верхний предел. Этот результат является теоремой Грёнвалла (Grönwall), опубликованной в 1913 году[7]. Его доказательство использует третью теорему Мертенса, которая утверждает, что
где p — простое.
В 1915 году Рамануджан доказал, что при выполнении гипотезы Римана неравенство
- (неравенство Робина)
выполняется для всех достаточно больших n[8]. В 1984 году Гай Робин доказал, что неравенство верно для всех n ≥ 5041 в том и только в том случае, если гипотеза Римана верна[9]. Это теорема Робина и неравенство стало широко известно после доказательства теоремы. Наибольшее известное число, нарушающее неравенство — это n=5040. Если гипотеза Римана верна, то нет чисел, больших этого и нарушающих неравенство. Робин показал, что в случае ошибочности гипотезы существует бесконечно много чисел n, нарушающих неравенство, и известно, что наименьшее из таких чисел n ≥ 5041 должно быть сверхизбыточным числом[10]. Было показано, что неравенство выполняется для больших нечётных свободных от квадратов чисел, и что гипотеза Римана эквивалентна выполнению неравенства для всех чисел n, делящихся на пятую степень простого числа[11]
Джефри Лагариас (Jeffrey Lagarias) в 2002 году доказал, что гипотеза Римана эквивалентна утверждению
для любого натурального n, где — n-е гармоническое число[12].
Робин доказал, что неравенство
выполняется для n ≥ 3 без каких-либо дополнительных условий.
Примечания
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77-171950 стр 46
- последовательность A000005 в OEIS
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766 , стр 58
- последовательность A000203 в OEIS
- последовательность A001065 в OEIS
- "Apostol Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001
- Grönwall, Thomas Hakon (1913), «Some asymptotic expressions in the theory of numbers», Transactions of the American Mathematical Society 14: 113—122, doi:10.1090/S0002-9947-1913-1500940-6
- Ramanujan, Srinivasa (1997), «Highly composite numbers, annotated by Jean-Louis Nicolas and Guy Robin», The Ramanujan Journal 1 (2): 119—153, doi:10.1023/A:1009764017495, ISSN 1382-4090, MR 1606180
- Robin, Guy (1984), «Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann», Journal de Mathématiques Pures et Appliquées, Neuvième Série 63 (2): 187—213, ISSN 0021-7824, MR 774171
- Akbary, Amir; Friggstad, Zachary (2009), «Superabundant numbers and the Riemann hypothesis», American Mathematical Monthly 116 (3): 273—275, doi:10.4169/193009709X470128
- YoungJu Choie, Nicolas Lichiardopol Pieter Moree Patrick Solé On Robin’s criterion for the Riemann hypothesis 2007 Journal de théorie des nombres de Bordeaux, ISSN=1246-7405, v19, issue 2, pages=357-372
- Lagarias, Jeffrey C. (2002), «An elementary problem equivalent to the Riemann hypothesis», The American Mathematical Monthly 109 (6): 534—543, doi:10.2307/2695443, ISSN 0002-9890, JSTOR 2695443, MR 19080
Ссылки
- Bach, Eric; Shallit, Jeffrey, Algorithmic Number Theory, volume 1, 1996, MIT Press. ISBN 0-262-02405-5, see page 234 in section 8.8.
- Weisstein, Eric W. Robin's Theorem (англ.) на сайте Wolfram MathWorld.
- Elementary Evaluation of Certain Convolution Sums Involving Divisor Functions PDF, авторы — Huard, Ou, Spearman, и Williams. Содержит элементарное (то есть не опирающееся на теорию модулярных форм) доказательство свертки суммы делителей, формулы для представления различными способами чисел как суммы треугольных чисел.