Дедекиндовы числа
Дедекиндовы числа — это быстро растущая последовательность целых чисел, названная именем Ричарда Дедекинда, который определил их в 1897. Число Дедекинда M(n) подсчитывает число монотонных булевых функций от n переменных. Эквивалентно, эти числа подсчитывают число антицепей подмножеств n-элементного множества, число элементов в свободной дистрибутивной решётке с n производящими, или число абстрактных симплициальных комплексов с n элементами.
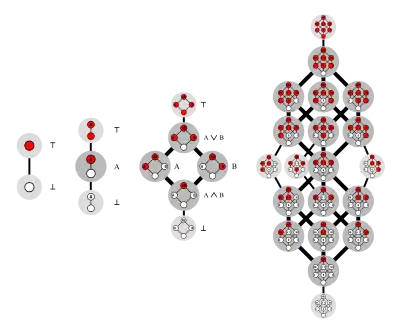
Точные асимптотические оценки M(n)[1][2][3] и точное выражение в виде суммы[4] известны. Однако задача Дедекинда вычисления значений M(n) остаётся сложной — не известно выражения в замкнутой форме для M(n) и точные значения M(n) найдены только для [5].
Определения
Булева функция — это функция, которая принимает в качестве входа n булевских переменных (то есть значений, которые могут быть либо false (ложь), либо true (истина), или, эквивалентно, бинарными значениями, которые могут быть либо 0, либо 1), и даёт в качестве выхода другую булевскую переменную. Функция монотонна, если для любой комбинации входа изменение одной входной переменной с false на true может привести только к изменению выхода с false на true, но не с true на false. Число Дедекинда M(n) — число различных монотонных булевых функций от n переменных.
Антицепь множеств (известная также как семейство Спенсера) — это семейство множеств, ни одно из которых не содержится в любом другом множестве. Если V является множеством n булевых переменных, антицепь A подмножеств V определяет монотонную булеву функцию f, когда значение f равно true для данного множества входов, если некоторое подмножество true входов функции f принадлежит A и false в другом случае. Обратно, любая монотонная булева функция определяет таким образом антицепь, минимальных подмножеств булевских переменных, которые вынуждают функцию дать значение true. Поэтому число Дедекинда M(n) равно числу различных антицепей подмножеств n-элементного множества[3].
Третий эквивалентный способ описания того же класса использует теорию решёток. Из двух монотонных булевых функций f и g мы можем найти две другие монотонные булевы функции и , их логическую конъюнкцию и логическую дизъюнкцию соответственно. Семейство всех монотонных булевых функций от n входов вместе с этими двумя операциями образует дистрибутивную решётку, задаваемую теоремой Биркгофа о представлении из частично упорядоченного множества подмножеств n переменных с частичным порядком включения множеств. Это построение даёт свободную дистрибутивную решётку с n генераторами[6]. Таким образом, числа Дедекинда подсчитывают число элементов в свободных дистрибутивных решётках[7][8] [9].
Числа Дедекинда подсчитывают также (на единицу больше) число абстрактных симплициальных комплексов на n элементах, семейства множеств со свойством, что любое подмножество множества в семействе также принадлежит семейству. Любая антицепь определяет симплициальный комплекс, семейство подмножеств членов антицепей, и обратно, максимальные симплексы в комплексах образуют антицепь[4].
Пример
Для n=2 существует шесть монотонных булевых функций и шесть антицепей подмножеств двухэлементного множества {x,y}:
- Функция , игнорирующая входные значения и всегда возвращающая false, соответствует пустой антицепи .
- Логическая конъюнкция соответствует антицепи { {x,y} }, содержащей единственное множество {x,y}.
- Функция , игнорирующая второй аргумент и возвращающая первый аргумент, соответствует антицепи { {x} }, содержащей единственное множество {x}.
- Функция , игнорирующая первый аргумент и возвращающая второй аргумент, соответствует антицепи { {y} }, содержащей единственное множество {y}.
- Логическая дизъюнкция соответствует антицепи { {x}, {y} }, содержащей два множества {x} и {y}.
- Функция , игнорирующая входные значения и всегда возвращающая true, соответствует антицепи , содержащей только пустое множество.
Значения
Точные значения чисел Дедекинда известны для :
- 2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 последовательность A000372 в OEIS.
Первые шесть этих чисел дал Чёрч[7]. M(6) вычислил Уорд[10], M(7) вычислили Чёрч[8] Берман и Кёлер[11], а M(8) вычислил Видерман[5].
Если n чётно, то M(n) также должно быть чётным[12]. Вычисление пятого числа Дедекинда опровергает гипотезу Гаррета Биркгофа, что M(n) всегда делится на [7].
Формула суммирования
Киселевич[4] переписал логическое определение антицепей в следующую арифметическую формулу для чисел Дедекинда:
где является -ым битом числа , который может быть записан с помощью округления вниз
Однако эта формула бесполезна для вычисления значений M(n) для больших n ввиду большого числа членов суммирования.
Асимптотика
Логарифм чисел Дедекинда можно оценить точно с помощью границ
Здесь неравенство слева подсчитывает число антицепей, в которых каждое множество имеет в точности элементов, а правое неравенство доказали Кляйтман и Марковский[1].
Коршунов[2] дал даже более точные оценки[9]
для чётных n, и
для нечётных n, где
и
Основная идея этих оценок заключается в том, что в большинстве антицепей все множества имеют размеры, очень близкие к n/2[9]. Для n=2, 4, 6, 8 формула Коршунова даёт оценку, которая имеет ошибку в 9,8 %, 10,2 %, 4,1 % и -3,3 %, соответственно[13].
Примечания
- Kleitman, Markowsky, 1975.
- Коршунов, 1981.
- Kahn, 2002.
- Kisielewicz, 1988.
- Wiedemann, 1991.
- Определение свободной дистрибутивной решётки, используемое здесь, разрешает в качестве операций на решётке любое конечное схождений и расхождений, включая пустые. Для свободной дистрибутивной решётки, в которой разрешены только попарные схождения и расхождения, следует исключать верхний и нижний элемент решётки и вычесть два из чисел Дедекинда.
- Church, 1940.
- Church, 1965.
- Zaguia, 1993.
- Ward, 1946.
- Berman, Köhler, 1976.
- Yamamoto, 1953.
- Brown, K. S., <https://www.mathpages.com/home/kmath094/kmath094.htm>
Литература
- Joel Berman, Peter Köhler. Cardinalities of finite distributive lattices // Mitt. Math. Sem. Giessen. — 1976. — Т. 121. — С. 103–124.
- Randolph Church. Numerical analysis of certain free distributive structures // Duke Mathematical Journal. — 1940. — Т. 6. — С. 732–734. — doi:10.1215/s0012-7094-40-00655-x..
- Randolph Church. Enumeration by rank of the free distributive lattice with 7 generators // Notices of the American Mathematical Society. — 1965. — Т. 11. — С. 724.. Как процитировано Видерманом (Wiedemann (1991)).
- Richard Dedekind. Über Zerlegungen von Zahlen durch ihre größten gemeinsamen Teiler // Gesammelte Werke. — 1897. — Т. 2. — С. 103–148.
- Jeff Kahn. Entropy, independent sets and antichains: a new approach to Dedekind's problem // Proceedings of the American Mathematical Society. — 2002. — Т. 130, вып. 2. — С. 371–378. — doi:10.1090/S0002-9939-01-06058-0.
- Andrzej Kisielewicz. A solution of Dedekind's problem on the number of isotone Boolean functions // Journal für die Reine und Angewandte Mathematik. — 1988. — Т. 386. — С. 139–144. — doi:10.1515/crll.1988.386.139.
- Kleitman D., Markowsky G. On Dedekind's problem: the number of isotone Boolean functions. II // Transactions of the American Mathematical Society. — 1975. — Т. 213. — С. 373–390. — doi:10.2307/1998052..
- Коршунов А. Д. О числе монотонных булевых функций // Проблемы кибернетики. — 1981. — Т. 38. — С. 5–108.
- Morgan Ward. Note on the order of free distributive lattices // Bulletin of the American Mathematical Society. — 1946. — Т. 52. — С. 423. — doi:10.1090/S0002-9904-1946-08568-7.
- Doug Wiedemann. A computation of the eighth Dedekind number // Order. — 1991. — Т. 8, вып. 1. — С. 5–6. — doi:10.1007/BF00385808..
- Koichi Yamamoto. Note on the order of free distributive lattices // Science Reports of the Kanazawa University. — 1953. — Т. 2, вып. 1. — С. 5–6.
- Nejib Zaguia. Isotone maps: enumeration and structure // Finite and Infinite Combinatorics in Sets and Logic (Proc. NATO Advanced Study Inst., Banff, Alberta, Canada, May 4, 1991) / Sauer N. W., Woodrow R. E., Sands B.. — Kluwer Academic Publishers, 1993. — С. 421–430.