Дизъюнкция
Дизъю́нкция (от лат. disjunctio — «разобщение»), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»[1].
| Дизъюнкция | |
|---|---|
| ИЛИ, OR | |
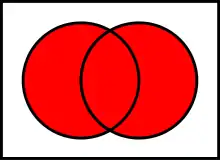 Диаграмма Венна | |
| Определение | |
| Таблица истинности | |
| Логический вентиль |
|
| Нормальные формы | |
| Дизъюнктивная | |
| Конъюнктивная | |
| Полином Жегалкина | |
| Принадлежность предполным классам | |
| Сохраняет 0 | Да |
| Сохраняет 1 | Да |
| Монотонна | Да |
| Линейна | Нет |
| Самодвойственна | Нет |
Дизъюнкция может быть операцией как бинарной (имеющей два операнда), так и -арной (имеющей операндов) для произвольного .
Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более двух префиксная и постфиксная записи экономичнее.
Обозначения
Наиболее часто встречаются следующие обозначения для операции дизъюнкции:
- || |
При этом обозначение , рекомендованное международным стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике[2]. Появилось оно не сразу: Джордж Буль, положивший начало систематическому применению символического метода к логике, не работал с дизъюнкцией (используя вместо неё строгую дизъюнкцию, которую обозначал знаком +), а Уильям Джевонс предложил для дизъюнкции знак ·|·. Эрнст Шрёдер и П. С. Порецкий вновь использовали знак +, но уже применительно к обычной дизъюнкции[3]. Символ как обозначение дизъюнкции впервые встречается в статье «Математическая логика, основанная на теории типов»[4] Бертрана Рассела (1908); он образован от лат. vel, что означает «или»[5][6].
Обозначение ⋁ для дизъюнкции было использовано и в раннем языке программирования Алгол 60[7]. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для дизъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения .OR. и | (с возможностью замены последнего на ключевое слово OR)[8]; в языках Паскаль и Ада используется зарезервированное слово or[9][10]; в языках C и C++ применяются обозначения | для побитовой дизъюнкции и || для логической дизъюнкции[11]).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что ), оказывается, что Таким образом, дизъюнкция оказывается частным случаем операции вычисления максимума; это открывает наиболее естественный способ определить операцию дизъюнкции в системах многозначной логики[12][13].
Булева алгебра
Логическая функция MAX в двухзначной (двоичной) логике называется дизъюнкция (логи́ческое «ИЛИ», логи́ческое сложе́ние или просто «ИЛИ»). При этом результат равен наибольшему операнду.
В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Таким образом, результат равен , если все операнды равны ; во всех остальных случаях результат равен .
| Таблица истинности | ||
|---|---|---|
Таблица истинности для тернарной (трёхоперандной) дизъюнкции:
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Многозначная логика
Операция, называемая в двоичной логике дизъюнкция, в многозначных логиках называется максимум: , где , а — значность логики. Возможны и другие варианты[чего?]. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов .
Название этой операции максимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия дизъюнкция, логи́ческое «ИЛИ», логическое сложе́ние и просто «ИЛИ» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для дизъюнкции:
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Схемотехника

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе есть «1»,
- «0» тогда и только тогда, когда на всех входах «0»
Теория множеств
С точки зрения теории множеств, дизъюнкция аналогична операции объединения.
Программирование
В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++/Perl/PHP логическое «ИЛИ» обозначается символом "||", а побитовое — символом "|". В языках Pascal/Delphi оба вида дизъюнкции обозначаются с использованием ключевого слова «or», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.
Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата или . Например:
if (a || b)
{
/* какие-то действия */
};
Результат будет равен , если оба операнда равны или . В любом другом случае результат будет равен .
При этом применяется стандартное соглашение: если значение левого операнда равно , то значение правого операнда не вычисляется (вместо может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую
{$B-}
или выключающую
{$B+}
подобное поведение. Например, если левый операнд проверяет необходимость вычисления правого операнда:
if (a == NULL || a->x == 0)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдёт разыменования нулевого указателя.
Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | |
| b = | |
| то | |
| a ИЛИ b = |
Связь с естественным языком
Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и (или)», иногда «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как , а «ложь» как .
Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — строгой дизъюнкции (исключающего «ИЛИ»).
Примечания
- Гутников В. С. . Интегральная электроника в измерительных приборах. — Л.: Энергия, 1974. — 144 с. — С. 14—16.
- Кондаков, 1975, с. 534.
- Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 320, 349, 352, 368.
- Russell B. Mathematical Logic as Based on the Theory of Types // American Journal of Mathematics. — 1908. — Vol. 30, no. 3. — P. 222—262.
- Earliest Uses of Symbols of Set Theory and Logic. // Website Jeff Miller Web Pages. Дата обращения: 5 февраля 2016.
- Кондаков, 1975, с. 149—150.
- Кондаков, 1975, с. 30.
- Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- Эллис М., Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.